前事不忘,后事之师——基于相似性进行剩余有效寿命预测的案例讲解
在上一篇文章中我们讲到了三种机电产品算命方法:相似模型法、退化模型法和生存模型法。
这一篇我们将使用相似模型法构建完整的剩余使用寿命(RUL)估计工作流程。该案例来自MATLAB的Similarity-Based Remaining Useful Life Estimation[1],在这里做一下流程梳理,对难点加一些讲解,并对代码添加了注释并列出了关键代码。
1.案例描述
数据集使用了PHM08挑战数据集,是涡轮风扇发动机退化模拟数据集。通过下述代码加载数据:
degradationData = helperLoadData('train.txt'); %从文本文件加载退化数据并转换为表格的单元格数组,专用于本案例。
degradationData(1:5) %查看退化数据前五组的大小
head(degradationData{1}) %查看第一组数据的前8行图1. 查看退化数据前五组的大小
图2. 查看第一组数据的前8行
退化数据都被加载到了degradationData变量中,从图1中可以看出,每组退化数据都包含26列数据,再从图2中看出,26列数据中包括了机器ID,时间戳,3个操作条件和21个传感器测量值的数据。
2.划分训练数据集和验证数据集
通过查看工作区,发现退化数据degradationData总共有218组,通常我们需要将这些数据分为训练数据集和验证数据集。为了更充分地使用所有数据,我们将所有数据平分为k份,然后每一份都做一次验证数据集(其余数据做训练集),这样我们就一共有了k对训练-验证数据,这种方法叫做k折交叉验证。代码实现方法如下:
rng('default') % 生成随机数,使用"default"是为了使用特定的随机数,这样大家的运行结果就都一样了
numEnsemble = length(degradationData);
numFold = 5; %交叉验证分区数,即k的值
cv = cvpartition(numEnsemble, 'KFold', numFold); %为数据创建交叉验证分区,K-折交叉验证
trainData = degradationData(training(cv, 1)); %读取第1组训练数据集
validationData = degradationData(test(cv, 1)); %读取第1组验证数据集获取感兴趣的变量组的数组名称后,进行数据样本可视化:
nsample = 10;
figure
helperPlotEnsemble(trainData, timeVariable, ... %专用函数,绘制conditionVariables(1:2)和dataVariables(1:2)的图像
[conditionVariables(1:2) dataVariables(1:2)], nsample) %即"op_setting_1","op_setting_2","sensor_1"和"sensor_2"
图3. 部分数据的可视化结果,每种颜色代表一组退化数据
3.工作状态聚类
从图3中看不出数据的退化趋势,下面我们将对退化特征进行提取。
trainDataUnwrap = vertcat(trainData{:}); %垂直串联数组,即将175数组退化数据拼接成1组
opConditionUnwrap = trainDataUnwrap(:, cellstr(conditionVariables)); %提取串联后的大数组的"op_setting_1","op_setting_2","op_setting_3"这三个一位数组
figure
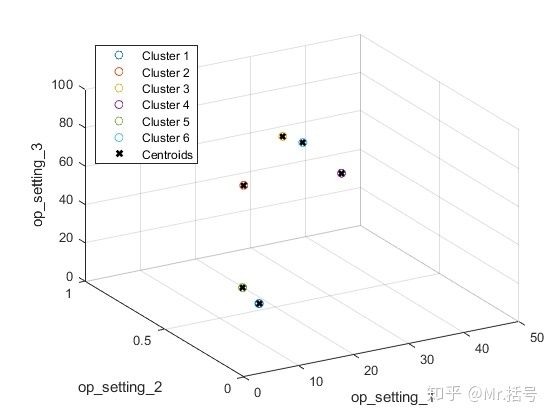
helperPlotClusters(opConditionUnwrap) %绘制三维散点图,查看聚类情况上边这段代码是将训练数据(共175组)串联成了一个大数组,然后分别以"op_setting_1", "op_setting_2", "op_setting_3"为x,y,z坐标绘制散点图。结果如下图:
图4. op_setting聚类情况
串联后的数据有3万多组,但是图上只有6个点,这是因为聚在一起的点相距太近,没有聚在一起的数据又离得太远,最终视觉效果就变成了只有6个点。如果不断地放大某个位置的点,就能看到聚在一起的密密麻麻的点了。这么分明的聚类结果是十分理想的。这说明"op_setting_1", "op_setting_2", "op_setting_3"的组合大致只有六组,所以后边我们将这六种组合对应的传感器的值分开分析。
下面我们将使用k均值聚类的方法计算对聚类结果进行定量分析,并找到各自的聚类质心:
opts = statset('Display', 'final'); %显示最终迭代结果
[clusterIndex, centers] = kmeans(table2array(opConditionUnwrap), 6, ... %调用kmeans函数进行k均值聚类
'Distance', 'sqeuclidean', 'Replicates', 5, 'Options', opts); %设置共分为6组,距离度量为欧氏距离,不同初始条件下重复计算5次
figure
helperPlotClusters(opConditionUnwrap, clusterIndex, centers) 图5. 可视化聚类结果和聚类质心
4.数据标准化
①计算各聚类下各传感器的均值,得到大小为6*21的数组(6为聚类数,21为传感器数)。
②计算各聚类下各传感器的标准差,得到大小为6*21的数组(6为聚类数,21为传感器数)。如果某组数据的标准差为0,则将该组数据统一设置为0,因为几乎恒定的传感器测量值对于剩余使用寿命估计没有用处。
③分别计算该条目数据至6个聚类中心的距离,并找到最近的聚类中心。
④对于每个传感器的测量值,减去“该聚类下该传感器”的平均值,再除以“该聚类下该传感器”的标准差。这种“减去均值再除以标准差”的方法叫做Z-score标准化,非常常用。经过这种处理后的数据均值为0,且符合正态分布。
centerstats = struct('Mean', table(), 'SD', table()); %初始化结构体,用于存储各传感器的均值和标准差
for v = dataVariables
centerstats.Mean.(char(v)) = splitapply(@mean, trainDataUnwrap.(char(v)), clusterIndex); %将个sensor数据划分到其所在的聚类,并求该聚类组的该传感器均值
centerstats.SD.(char(v)) = splitapply(@std, trainDataUnwrap.(char(v)), clusterIndex); %将个sensor数据划分到其所在的聚类,并求该聚类组的该传感器标准差
end
trainDataNormalized = cellfun(@(data) regimeNormalization(data, centers, centerstats), ... %进行数据规范化
trainData, 'UniformOutput', false);
figure
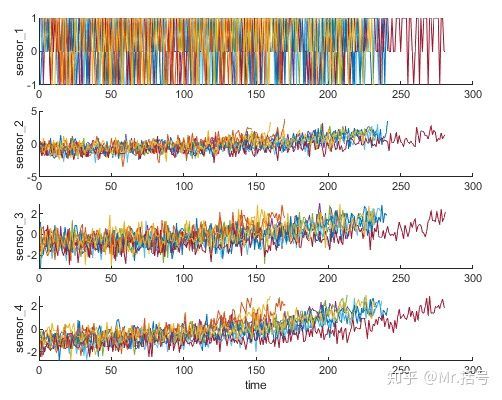
helperPlotEnsemble(trainDataNormalized, timeVariable, dataVariables(1:4), nsample) %规范化后的退化数据可视化图6. 规范化后的退化数据可视化
为什么标准化处理后退化趋势就显现出来了呢?是因为之前6种运行状态下的传感器数据混杂在一起,互相干扰,或者说趋势性被不同运行状态引起的干扰淹没了;在我们将6种状态下的传感器区分开之后,分别进行标准化,就剔除掉了运行状态所造成的差异性,使得传感器数据在不同时间上可对比。
5.趋势分析
从上图中可以看到,某些传感器退化趋势明显,某些不太明显。这里我们选择最具趋势性的传感器测量值,构建健康指数进行预测。对每个传感器测量值构建线性退化模型,并对信号的斜率的绝对值进行排序。
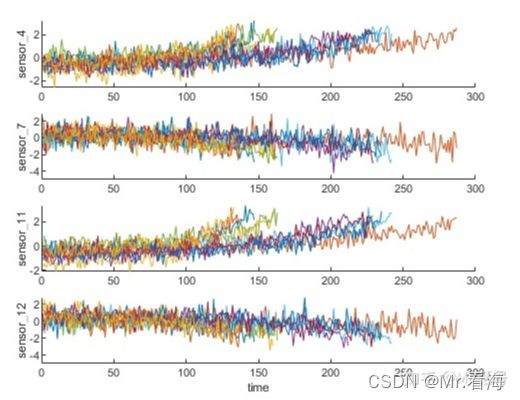
最终选出8组退化趋势的传感器,其中四组的数据如下:
图7. 4组退化较为明显的传感器数据
需要注意的是,有些传感器数据呈上升趋势,有些呈下降趋势,而我们是以斜率的绝对值为选取标准的。
6.构建表征健康度的指标
我们需要将选出的这些传感器数据融合到一个健康指标中,并通过该指标训练基于相似性的模型。
假设所有的故障数据都是从健康状况开始的,开始时的健康状况设为1,失效时的健康状况为0。那么所有数据对应的健康状况都是从1下降至0。其中10组数据的健康指标的变化趋势如下:
图8. 10组数据的健康指标变化趋势
下面开始构建健康状况的线性回归模型:
①我们之前选定了8个退化规律最明显的传感器,建立这8个传感器与健康状况的线性模型。
②y=ax+b这种线性回归模型大家都知道吧,在这个例子里,y就是图8中的健康指标,x就是8个传感器的数值,而a和b则是我们要估计的回归参数。与平时常用的不同的是,这里a是个1*8的矩阵,x也是个8*n的矩阵(n为每个传感器采集到的数据长度)。
③所以这个线性模型也可以写成:
需要估计的就是a1~a8和b这九个参数。可以通过下述代码实现:
trainDataNormalizedUnwrap = vertcat(trainDataNormalized{:}); %将标准化后的数据垂直串联为一个大数组
sensorToFuse = dataVariables(sensorTrended); %退化最明显的八组传感器
X = trainDataNormalizedUnwrap{:, cellstr(sensorToFuse)}; %8组传感器数值
y = trainDataNormalizedUnwrap.health_condition; %健康指标
regModel = fitlm(X,y); %进行拟合
bias = regModel.Coefficients.Estimate(1) %查看常数项
weights = regModel.Coefficients.Estimate(2:end) %查看系数然后将估计的参数带入模型中,重新得到健康指标。这期间还需要进行滑动平均平滑处理和将健康指标数据移动到从1开始。
重构后的健康指标
7.使用同样的方法处理验证集数据
将验证数据集数据进行标准化,并同样带入上一节中得到的线性模型中。此时的健康指标为:
验证集数据按照模型重构后的健康指标
8.建立相似性RUL模型
现在使用训练数据建立一个基于残差的相似性RUL模型。在此设置中,模型试用二次多项式拟合每个融合数据。
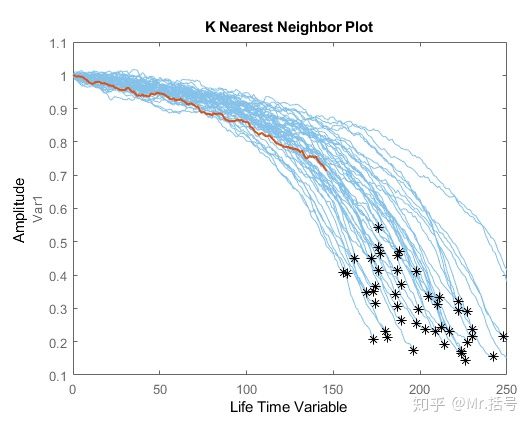
给定验证数据集中的几个集合成员,模型将找到训练数据集中最近的50个集合成员,拟合基于50个集合成员的概率分布,并使用分布中的中值作为RUL的估计。代码如下:
mdl = residualSimilarityModel(...
'Method', 'poly2',... %使用poly2方法
'Distance', 'absolute',... %绝对值距离
'NumNearestNeighbors', 50,... %集合成员为50
'Standardize', 1);
fit(mdl, trainDataFused); %拟合模型9.性能评估
为了评估相似性rul模型,使用50%、70%和90%的样本验证数据来预测其RUL。
bpidx = 1; %使用50%的区间
validationDataTmp50 = validationDataTmp(1:ceil(end*breakpoint(bpidx)),:); % 50%区间内的健康指标
trueRUL = length(validationDataTmp) - length(validationDataTmp50); % 真实剩余寿命
[estRUL, ciRUL, pdfRUL] = predictRUL(mdl, validationDataTmp50); % 得到估计的剩余寿命、置信区间和RUL概率密度的估计值(1)50%截段的数据验证
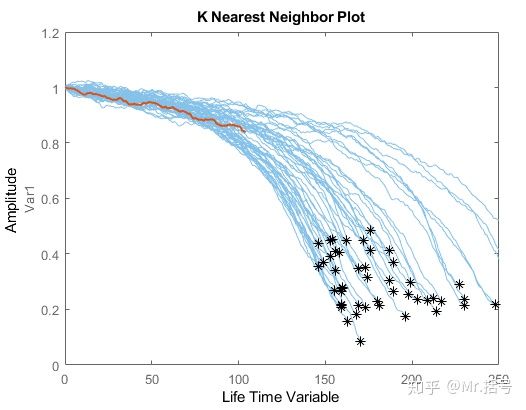
随便选择一组验证数据,并截取其前50%的数据,绘制下图:红线为该组被截断50%的数据,蓝线为验证数据集其他组数据的退化曲线。
选定的截断数据与其周围数据
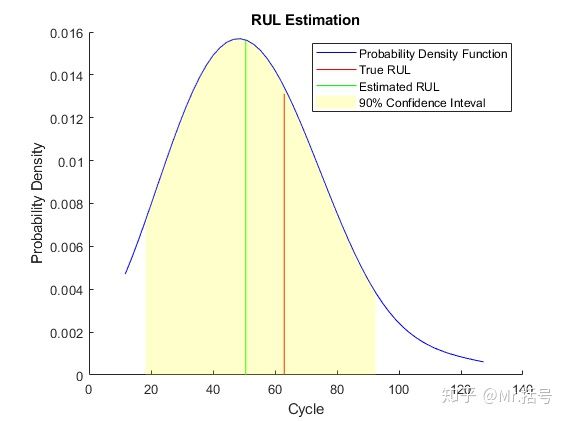
将估计的RUL、真实RUL和估计RUL的概率分布进行比较。如下图:
(2)70%截段的数据验证
(3)90%截段的数据验证
通过50%、70%、90%估计寿命的结果对比,发现随着验证数据比例的增加,寿命的估计值也会更准确(当然了)。
10.整体评价
第9步中是对某一组退化数据进行的预测,现在对整个验证数据集重复相同的评估程序,并计算每个断点的估计RUL和真实RUL之间的误差。
(1)绘制每个断点的误差直方图及其分布:
随着观测的数据越来越多(从50%~90%),误差越来越集中于0附近。
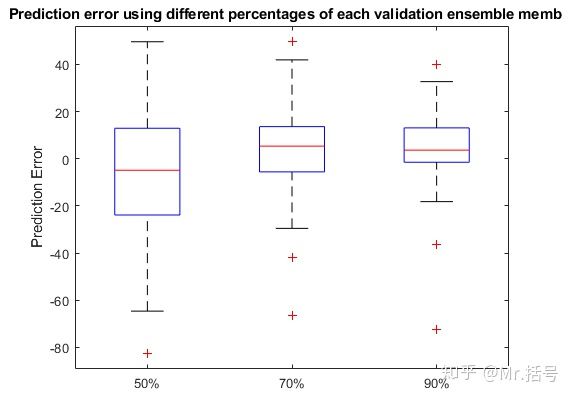
(2)绘制箱型图
箱型图是一种用作显示一组数据分散情况资料的统计图。它主要用于反映原始数据分布的特征,还可以进行多组数据分布特征的比较。具体介绍可以参看:https://blog.csdn.net/uinglin/article/details/79895993
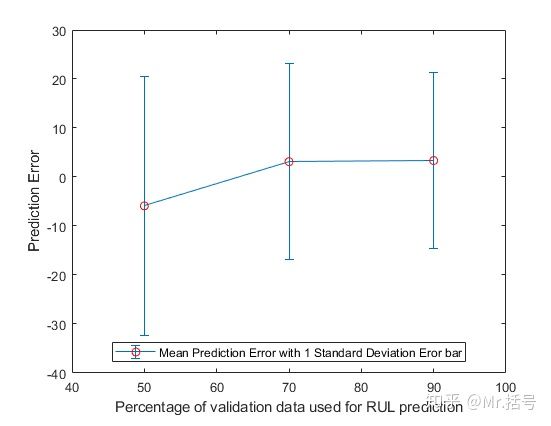
(3)绘制误差棒图
误差棒是数据可变性的图形表示,并用于图表以指示所报告的测量中的误差或不确定性。如下图中每个竖线代表了预测的平均误差以及一个标准差的范围。可以看出,随着观测的数据越来越多,预测误差均值越来越小,误差范围也越来越小。
总结
总的来说,通过50%、70%、90%估计寿命的结果对比,发现随着验证数据比例的增加,寿命的估计值也会更准确(当然了)。
这个方法的关键之处在于,需要有比较大量的失效数据,经过数据聚类→数据标准化→选取退化趋势最明显的传感器→构建线性退化模型→建立相似性RUL模型→进行预测 这些步骤可以实现预测。这个大量失效数据的条件在某些产品中是不容易得到的,但是如果有这些数据,预测结果还是比较可靠的。
如果想要获取经博主添加注释后的代码和数据集,关注我的公众号“看海的城堡”,微信号为“khscience”,回复“相似性”就能拿到啦,公众号里可能还会有更多有趣的东西分享。
[1] https://ww2.mathworks.cn/help/predmaint/ug/similarity-based-remaining-useful-life-estimation.html