【决策树】

决策树原理

1.决策树算法模型：
决策树模型是运用于分类以及回归的一种树结构。决策树由节点和有向边组成，一般一棵决策树包含一个根节点、若干内部节点和若干叶节点。决策树的决策过程需要从决策树的根节点开始，待测数据与决策树中的特征节点进行比较，并按照比较结果选择选择下一比较分支，直到叶子节点作为最终的决策结果。

(1).内部节点：对应于一个属性测试
(2).叶节点：对应于决策结果
(3).根节点包含样本全集；
(4).每个节点包括的样本集合根据属性测试的结果被划分到子节点中；
根节点到每个叶节点的路径对应对应了一个判定测试路径；
示例：

决策树学习算法：

(1).特征选择
(2).决策树生成
(3).决策树剪枝
1.特征选择：
特征选择也即选择最优划分属性，从当前数据的特征中选择一个特征作为当前节点的划分标准。我们希望在不断划分的过程中，决策树的分支节点所包含的样本尽可能属于同一类，即节点的“纯度”越来越高。而选择最优划分特征的标准不同，也导致了决策树算法的不同。
2.特征划分：
(1).信息熵
(2).信息增益
(3).信息增益率
(4).基尼指数
熵：
熵(entropy)是表示随机变量不确定性的度量，设X是一个取有限值的离散随机变量，其概率分布为:
$P(X=x_i)=p_i,i=1,2,...,n$
则随机变量 X的熵定义为:
$$H(x)=-\sum _{i=1}^n{p}_{i}log{p}_i$$
熵越大，随机变量的不确定性越大。为了能够更好地理解熵的意义，我们下面举一个例子来说明。
当随机变量只取两个值，如1，0时，即 X的分布为
$$P(X=1)=p,P(X=0)=1-p,0\le p\le 1$$
熵:
$$H(p)=-plog2p-(1-p)log2(1-p)$$
信息增益：
$信息增益表示得知特征XX的信息而使得类Y的信息的不确定性减少程度。接下来给出定义，特征AA对训练数据集DD的信息增益g(D,A)g(D,A),为集合DD的熵H(D)H(D)与特征AA给定条件下DD的条件熵H(D|A)H(D|A)之差$，
即 :
$$g(D,A)=H(D)-H(D|A)$$
信息增益的算法:

(1).输入：训练数据集D，特征A
(2).输出：特征A对训练数据集D的信息增益g(D,A)
熵H(D)计算：
$$H(D)=-\sum _{k=1}^K\frac{C_k}{D}log2\frac{|C_k|}{|D|}$$
(2):计算特征A对训练数据集D的条件熵H(D|A)
$$H(D|A)-\sum _{k=1}^{K}H(D_i)=-\sum _{i=1}^n\frac{C_k}{D}f\frac{D_I}{D}\sum _{k=1}^K\frac{|D_{ik}|}{|D_i|}log2\frac{D_{ik}}{D_i}$$
计算信息增益:
$$g(D,A)=H(D)-H(D|A)$$

习题5.1

1.样表：

第1步：C4.5的生成算法（书中第78页）
输入：训练数据集DD，特征集AA阈值\epsilonϵ；
输出：决策树TT。
$（1）如果DD中所有实例属于同一类C_k，则置T为单结点树，并将C_k作为该结点的类，返回T；$
$（2）如果A=\varnothing ，则置T为单结点树，并将DD中实例数最大的类C_k作为该结点的类，返回T；$
$(3）否则，按式g_R(D,A)=\frac{g(D,A)}{H_A(D)}gR(D,A)=HA(D)g(D,A)计算AA中各特征对DD的信息增益比，选择信息增益比最大的特征A_g；$
$（4）如果A_g的信息增益比小于阈值ϵϵ，则置T为单结点树，并将D中实例数最大的类C_k作为该结点的类，返回T；$
$（5）否则，对A_g的每一可能值a_i，依A_g=a_i将D分割为子集若干非空D_i，将D_i中实例数最大的类作为标记，构建子结点，由结点及其子结点构成树T，返回T；$
$（6）对结点ii，以D_i为训练集，以A-\{A_g\}A-Ag为特征集，递归地调用步(1)步(5)，得到子树T_i，返回T_i$
​第2步：调用sklearn的DecisionTreeClassifier类构建决策树

from sklearn.tree import DecisionTreeClassifier
from sklearn import preprocessing
import numpy as np
import pandas as pd

from sklearn import tree
import graphviz

features = ["年龄", "有工作", "有自己的房子", "信贷情况"]
X_train = pd.DataFrame([
    ["青年", "否", "否", "一般"],
    ["青年", "否", "否", "好"],
    ["青年", "是", "否", "好"],
    ["青年", "是", "是", "一般"],
    ["青年", "否", "否", "一般"],
    ["中年", "否", "否", "一般"],
    ["中年", "否", "否", "好"],
    ["中年", "是", "是", "好"],
    ["中年", "否", "是", "非常好"],
    ["中年", "否", "是", "非常好"],
    ["老年", "否", "是", "非常好"],
    ["老年", "否", "是", "好"],
    ["老年", "是", "否", "好"],
    ["老年", "是", "否", "非常好"],
    ["老年", "否", "否", "一般"]
])
y_train = pd.DataFrame(["否", "否", "是", "是", "否",
                        "否", "否", "是", "是", "是",
                        "是", "是", "是", "是", "否"])
class_names = [str(k) for k in np.unique(y_train)]
# 数据预处理
le_x = preprocessing.LabelEncoder()
le_x.fit(np.unique(X_train))
X_train = X_train.apply(le_x.transform)
# 调用sklearn的DecisionTreeClassifier建立决策树模型
model_tree = DecisionTreeClassifier()
# 训练模型
model_tree.fit(X_train, y_train)

# 导出决策树的可视化文件，文件格式是dot
dot_data = tree.export_graphviz(model_tree, out_file=None,
                                feature_names=features,
                                class_names=class_names,
                                filled=True, rounded=True,
                                special_characters=True)
# 使用graphviz包，对决策树进行展示
graph = graphviz.Source(dot_data)
# 可使用view方法展示决策树
# 中文乱码：需要对源码_export.py文件（文件路径：sklearn/tree/_export.py）修改，
# 在文件第451行中将helvetica改成SimSun
graph
# 打印决策树
tree_text = tree.export_text(model_tree, feature_names=features)
print(tree_text)

输出结果：

|--- 有自己的房子 <= 3.00
|   |--- 有工作 <= 3.00
|   |   |--- class: 否
|   |--- 有工作 >  3.00
|   |   |--- class: 是
|--- 有自己的房子 >  3.00
|   |--- class: 是

第3步：自编程实现C4.5算法生成决策树

import json
from collections import Counter

import numpy as np


# 节点类
class Node:
    def __init__(self, node_type, class_name, feature_name=None,
                 info_gain_ratio_value=0.0):
        # 结点类型（internal或leaf）
        self.node_type = node_type
        # 特征名
        self.feature_name = feature_name
        # 类别名
        self.class_name = class_name
        # 子结点树
        self.child_nodes = []
        # Gini指数值
        self.info_gain_ratio_value = info_gain_ratio_value

    def __repr__(self):
        return json.dumps(self, indent=3, default=lambda obj: obj.__dict__, ensure_ascii=False)

    def add_sub_tree(self, key, sub_tree):
        self.child_nodes.append({"condition": key, "sub_tree": sub_tree})
        class MyDecisionTree:
    def __init__(self, epsilon):
        self.epsilon = epsilon
        self.tree = None

    def fit(self, train_set, y, feature_names):
        features_indices = list(range(len(feature_names)))
        self.tree = self._fit(train_set, y, features_indices, feature_names)
        return self

    # C4.5算法
    def _fit(self, train_data, y, features_indices, feature_labels):
        LEAF = 'leaf'
        INTERNAL = 'internal'
        class_num = len(np.unique(y))

        # （1）如果训练数据集所有实例都属于同一类Ck
        label_set = set(y)
        if len(label_set) == 1:
            # 将Ck作为该结点的类
            return Node(node_type=LEAF, class_name=label_set.pop())

        # （2）如果特征集为空
        # 计算每一个类出现的个数
        class_len = Counter(y).most_common()
        (max_class, max_len) = class_len[0]

        if len(features_indices) == 0:
            # 将实例数最大的类Ck作为该结点的类
            return Node(LEAF, class_name=max_class)

        # （3）按式(5.10)计算信息增益，并选择信息增益最大的特征
        max_feature = 0
        max_gda = 0
        D = y.copy()
        # 计算特征集A中各特征
        for feature in features_indices:
            # 选择训练集中的第feature列（即第feature个特征）
            A = np.array(train_data[:, feature].flat)
            # 计算信息增益
            gda = self._calc_ent_grap(A, D)
            if self._calc_ent(A) != 0:
                # 计算信息增益比
                gda /= self._calc_ent(A)
            # 选择信息增益最大的特征Ag
            if gda > max_gda:
                max_gda, max_feature = gda, feature

        # （4）如果Ag信息增益小于阈值
        if max_gda < self.epsilon:
            # 将训练集中实例数最大的类Ck作为该结点的类
            return Node(LEAF, class_name=max_class)

        max_feature_label = feature_labels[max_feature]

        # （6）移除已选特征Ag
        sub_feature_indecs = np.setdiff1d(features_indices, max_feature)
        sub_feature_labels = np.setdiff1d(feature_labels, max_feature_label)

        # （5）构建非空子集
        # 构建结点
        feature_name = feature_labels[max_feature]
        tree = Node(INTERNAL, class_name=None, feature_name=feature_name,
                    info_gain_ratio_value=max_gda)

        max_feature_col = np.array(train_data[:, max_feature].flat)
        # 将类按照对应的实例数递减顺序排列
        feature_value_list = [x[0] for x in Counter(max_feature_col).most_common()]
        # 遍历Ag的每一个可能值ai
        for feature_value in feature_value_list:
            index = []
            for i in range(len(y)):
                if train_data[i][max_feature] == feature_value:
                    index.append(i)

            # 递归调用步（1）~步（5），得到子树
            sub_train_set = train_data[index]
            sub_train_label = y[index]
            sub_tree = self._fit(sub_train_set, sub_train_label, sub_feature_indecs, sub_feature_labels)
            # 在结点中，添加其子结点构成的树
            tree.add_sub_tree(feature_value, sub_tree)

        return tree

    # 计算数据集x的经验熵H(x)
    def _calc_ent(self, x):
        x_value_list = set([x[i] for i in range(x.shape[0])])
        ent = 0.0
        for x_value in x_value_list:
            p = float(x[x == x_value].shape[0]) / x.shape[0]
            logp = np.log2(p)
            ent -= p * logp

        return ent

    # 计算条件熵H(y/x)
    def _calc_condition_ent(self, x, y):
        x_value_list = set([x[i] for i in range(x.shape[0])])
        ent = 0.0
        for x_value in x_value_list:
            sub_y = y[x == x_value]
            temp_ent = self._calc_ent(sub_y)
            ent += (float(sub_y.shape[0]) / y.shape[0]) * temp_ent

        return ent

    # 计算信息增益
    def _calc_ent_grap(self, x, y):
        base_ent = self._calc_ent(y)
        condition_ent = self._calc_condition_ent(x, y)
        ent_grap = base_ent - condition_ent

        return ent_grap

    def __repr__(self):
        return str(self.tree)
        # 表5.1的训练数据集
feature_names = np.array(["年龄", "有工作", "有自己的房子", "信贷情况"])
X_train = np.array([
    ["青年", "否", "否", "一般"],
    ["青年", "否", "否", "好"],
    ["青年", "是", "否", "好"],
    ["青年", "是", "是", "一般"],
    ["青年", "否", "否", "一般"],
    ["中年", "否", "否", "一般"],
    ["中年", "否", "否", "好"],
    ["中年", "是", "是", "好"],
    ["中年", "否", "是", "非常好"],
    ["中年", "否", "是", "非常好"],
    ["老年", "否", "是", "非常好"],
    ["老年", "否", "是", "好"],
    ["老年", "是", "否", "好"],
    ["老年", "是", "否", "非常好"],
    ["老年", "否", "否", "一般"]
])
y = np.array(["否", "否", "是", "是", "否",
              "否", "否", "是", "是", "是",
              "是", "是", "是", "是", "否"])

dt_tree = MyDecisionTree(epsilon=0.1)
dt_tree.fit(X_train, y, feature_names)
dt_tree
Copy to clipboardErrorCopied
{
   "node_type": "internal",
   "feature_name": "有自己的房子",
   "class_name": null,
   "child_nodes": [
      {
         "condition": "否",
         "sub_tree": {
            "node_type": "internal",
            "feature_name": "年龄",
            "class_name": null,
            "child_nodes": [
               {
                  "condition": "否",
                  "sub_tree": {
                     "node_type": "leaf",
                     "feature_name": null,
                     "class_name": "否",
                     "child_nodes": [],
                     "info_gain_ratio_value": 0.0
                  }
               },
               {
                  "condition": "是",
                  "sub_tree": {
                     "node_type": "leaf",
                     "feature_name": null,
                     "class_name": "是",
                     "child_nodes": [],
                     "info_gain_ratio_value": 0.0
                  }
               }
            ],
            "info_gain_ratio_value": 1.0
         }
      },
      {
         "condition": "是",
         "sub_tree": {
            "node_type": "leaf",
            "feature_name": null,
            "class_name": "是",
            "child_nodes": [],
            "info_gain_ratio_value": 0.0
         }
      }
   ],
   "info_gain_ratio_value": 0.4325380677663126
}

习题5.2

已知如表5.2所示的训练数据，试用平方误差损失准则生成一个二叉回归树。
表5.2 训练数据表

第1步：算法5.5的最小二乘回归树生成算法（书中第82页）
决策树的生成就是递归地构建二叉决策树的过程，对回归树用平方误差最小化准则，对分类树用基尼指数（Gini index）最小化准则，进行特征选择，生成二叉树。

算法5.5（最小二乘回归树生成算法）
输入：训练数据集D
输出：回归树f(x)
在训练数据集所在的输入空间中，递归地将每个区域划分为两个子区域并决定每个子区域上的输出值，构建二叉决策树；
(1)选择最优切分变量j与切分点s，求解

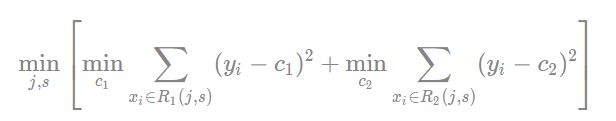
遍历变量jj，对固定的切分变量jj扫描切分点ss，选择使得上式达到最小值的对(j,s)(j,s)
(2)用选定的对(j,s)(j,s)划分区域并决定相应的输出值：

3)继续对两个子区域调用步骤(1),(2)，直至满足停止条件
(4)将输入空间划分为MM个区域$R_1,R_2,\cdots ,R_M$生成决策树：

第2步：编写代码，实现算法，并用表5.2训练数据进行验证

import json

import numpy as np


# 节点类
class Node:
    def __init__(self, value, feature, left=None, right=None):
        self.value = value.tolist()
        self.feature = feature.tolist()
        self.left = left
        self.right = right

    def __repr__(self):
        return json.dumps(self, indent=3, default=lambda obj: obj.__dict__, ensure_ascii=False)
 class MyLeastSquareRegTree:
    def __init__(self, train_X, y, epsilon):
        # 训练集特征值
        self.x = train_X
        # 类别
        self.y = y
        # 特征总数
        self.feature_count = train_X.shape[1]
        # 损失阈值
        self.epsilon = epsilon
        # 回归树
        self.tree = None

    def _fit(self, x, y, feature_count):
        # （1）选择最优切分点变量j与切分点s，得到选定的对(j,s)，并解得c1，c2
        (j, s, minval, c1, c2) = self._divide(x, y, feature_count)
        # 初始化树
        tree = Node(feature=j, value=x[s, j], left=None, right=None)
        # 用选定的对(j,s)划分区域，并确定响应的输出值
        if minval < self.epsilon or len(y[np.where(x[:, j] <= x[s, j])]) <= 1:
            tree.left = c1
        else:
            # 对左子区域调用步骤（1）、（2）
            tree.left = self._fit(x[np.where(x[:, j] <= x[s, j])],
                                  y[np.where(x[:, j] <= x[s, j])],
                                  self.feature_count)
        if minval < self.epsilon or len(y[np.where(x[:, j] > s)]) <= 1:
            tree.right = c2
        else:
            # 对右子区域调用步骤（1）、（2）
            tree.right = self._fit(x[np.where(x[:, j] > x[s, j])],
                                   y[np.where(x[:, j] > x[s, j])],
                                   self.feature_count)
        return tree

    def fit(self):
        self.tree = self._fit(self.x, self.y, self.feature_count)
        return self

    @staticmethod
    def _divide(x, y, feature_count):
        # 初始化损失误差
        cost = np.zeros((feature_count, len(x)))
        # 公式5.21
        for i in range(feature_count):
            for k in range(len(x)):
                # k行i列的特征值
                value = x[k, i]
                y1 = y[np.where(x[:, i] <= value)]
                c1 = np.mean(y1)
                y2 = y[np.where(x[:, i] > value)]
                if len(y2) == 0:
                    c2 = 0
                else:
                    c2 = np.mean(y2)
                y1[:] = y1[:] - c1
                y2[:] = y2[:] - c2
                cost[i, k] = np.sum(y1 * y1) + np.sum(y2 * y2)
        # 选取最优损失误差点
        cost_index = np.where(cost == np.min(cost))
        # 所选取的特征
        j = cost_index[0][0]
        # 选取特征的切分点
        s = cost_index[1][0]
        # 求两个区域的均值c1,c2
        c1 = np.mean(y[np.where(x[:, j] <= x[s, j])])
        c2 = np.mean(y[np.where(x[:, j] > x[s, j])])
        return j, s, cost[cost_index], c1, c2

    def __repr__(self):
        return str(self.tree)
Copy to clipboardErrorCopied
train_X = np.array([[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]]).T
y = np.array([4.50, 4.75, 4.91, 5.34, 5.80, 7.05, 7.90, 8.23, 8.70, 9.00])

model_tree = MyLeastSquareRegTree(train_X, y, epsilon=0.2)
model_tree.fit()
model_tree
Copy to clipboardErrorCopied
{
   "value": 5,
   "feature": 0,
   "left": {
      "value": 3,
      "feature": 0,
      "left": 4.72,
      "right": 5.57
   },
   "right": {
      "value": 7,
      "feature": 0,
      "left": {
         "value": 6,
         "feature": 0,
         "left": 7.05,
         "right": 7.9
      },
      "right": {
         "value": 8,
         "feature": 0,
         "left": 8.23,
         "right": 8.85
      }
   }
}

根据上面程序的输出，可得到用平方误差损失准则生成一个二叉回归树：

参考资料datawhale组队学习