Tensorflow笔记——神经网络优化

目录

 1.常用函数： 

（1）tf.cast

（2）tf.random.normal

（3）tf.where

2.神经网络复杂度

(1)时间复杂度

(2)空间复杂度

3.学习率衰减策略

(1)指数衰减

(2)分段常数衰减

4.激活函数

（1）sigmoid

（2）tanh

（4）Leaky ReLU

（5）softmax

（6）建议

5.损失函数

（1）均方误差损失函数

（2）交叉熵损失函数

tf.keras.losses.CategoricalCrossentropy

 tf.nn.softmax_cross_entropy_with_logits

 tf.nn.sparse_softmax_cross_entropy_with_logits

（3）自定义损失函数

6.欠拟合与过拟合

7.优化器 

---

 1.常用函数： 

（1）tf.cast

tf.cast(
    x, dtype, name=None
)

功能：转换数据（张量）类型 

参数
x	待转换的数据（张量）
dtype	目标数据类型
name	操作的名称（可选）。

 返回：数据类型为dtype，shape与x相同的张量

x = tf.constant([1.8, 2.2], dtype=tf.float32)
print(tf.cast(x, tf.int32))

 tf.Tensor([1 2], shape=(2,), dtype=int32)

---

 

（2）tf.random.normal

tf.random.normal(
    shape,
    mean=0.0,
    stddev=1.0,
    dtype=tf.dtypes.float32,
    seed=None,
    name=None
)

功能：生成服从正态分布的随机值 

参数
shape	输出张量的形状。
mean	正态分布的均值。
stddev	正态分布的标准差。
dtype	输出张量的数据类型。
seed	用于为分布创建随机种子。
name	操作的名称（可选）。

返回：满足指定shape并且服从正态分布的张量

print(tf.random.normal([3,2], 0, 1, tf.float32))

 tf.Tensor(
[[-0.4142421   1.6383653 ]
 [ 0.5216099  -0.5298042 ]
 [ 0.47332713 -1.0492674 ]], shape=(3, 2), dtype=float32)

---

 

（3）tf.where

tf.where(
    condition, x=None, y=None, name=None
)

功能：根据condition，取x或y中的值。如果为True，对应位置取x的值；如果为False，对应位置取y的值

参数
condition	一个 tf. dtype bool 的张量，或任何数字 dtype。
x	与y shape相同的张量。
y	与x shape相同的张量。
name	操作的名称（可选）。

 返回：shape与x相同的张量。

print(tf.where([True, False, True],
         x=[[1, 2, 3],
            [4, 5, 6],
            [7, 8, 9]],
         y=[[100],
            [200],
            [300]]
))

 tf.Tensor(
[[  1 100   3]
 [  4 200   6]
 [  7 300   9]], shape=(3, 3), dtype=int32)

---

 

2.神经网络复杂度

(1)时间复杂度

模型的运算次数，可用浮点运算次数（FPLOPs，FLoating-point Operations）或者乘加运算次数衡量。如一个两层神经网络，输入层为3，隐藏层为4，输出层为2，那么其时间复杂度为3x4+4x2=20

---

 

(2)空间复杂度

空间复杂度（访存量），严格来讲包括两部分：总参数量+各层输出特征图

参数量：模型重所有带参数的层的权重参数总量

特征图：模型在实时运行过程重每层计算出的输出特征图大小

---

 

3.学习率衰减策略

TensorFlow官方网址：https://tensorflow.google.cn/api_docs/python/tf/keras/optimizers/schedules

(1)指数衰减

TensorFlow API：

tf.keras.optimizers.schedules.ExponentialDecay(
    initial_learning_rate, decay_steps, decay_rate, staircase=False, name=None
)

参数
initial_learning_rate	标量或 Python 编号。初始学习率。float32float64Tensor
decay_steps	标量或 Python 编号。必须为阳性。请参阅上面的衰减计算。int32int64Tensor
decay_rate	标量或 Python 编号。衰减率。float32float64Tensor
staircase	布尔。如果以离散间隔衰减学习速率True
name	字符串。操作的可选名称。默认为“指数十进制”。

指数衰减学习率是先使用较大的学习率来快速得到一个较优的解，然后随着迭代的继续，逐步减小学习率，使得模型在训练后期更加稳定。指数型学习率衰减法是最常用的衰减方法，在大量模型重广泛使用。

例：

# -*- coding: utf-8 -*-
# @Time : 2022/8/9 18:49
# @Author : 中意灬
# @FileName: 指数衰减学习策略.py
# @Software: PyCharm
import tensorflow as tf
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
N=400#迭代次数
lr_schedule=tf.keras.optimizers.schedules.ExponentialDecay(
    initial_learning_rate=0.5,#初始学习率
    decay_steps=10,#衰减步长，即每十次衰减一次
    decay_rate=0.9,#衰减率，即以基数的0.9衰减
    staircase=False
)
y=[]
for global_step in range(N):
    lr=lr_schedule(global_step)
    y.append(lr)
x=range(N)
plt.figure()
plt.plot(x,y,'r-')
plt.xlabel('步长')
plt.ylabel('学习率')
plt.title('指数衰减')
plt.show()

 

 

---

 

(2)分段常数衰减

TensorFlow API：

tf.keras.optimizers.schedules.PiecewiseConstantDecay(
    boundaries, values, name=None
)

参数
boundaries	具有严格递增条目的 s 或 s 或 s 的列表，并且所有元素都具有与优化程序步骤相同的类型。Tensorintfloat
values	s 或 s 或 s 的列表，它指定 由 定义的间隔的值。它应该比 多一个元素，并且所有元素都应该具有相同的类型。Tensorfloatintboundariesboundaries
name	字符串。操作的可选名称。默认为“分段常量”。

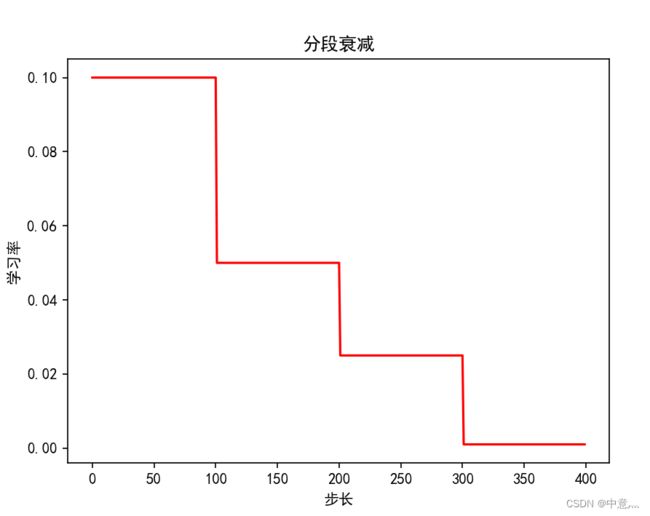
分段常数衰减可以让调试人员针对不同任务设置不同的学习率，进行精细调参，在任意步长后下降任意数值的learning rate，要求调试人员对模型和数据集有深刻认识。

# -*- coding: utf-8 -*-
# @Time : 2022/8/23 9:54
# @Author : 中意灬
# @FileName: 分段常数衰减学习率策略.py
# @Software: PyCharm
import tensorflow as tf
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
N=400
lr_schedule=tf.keras.optimizers.schedules.PiecewiseConstantDecay(
    boundaries=[100,200,300],
    values=[0.1,0.05,0.025,0.001]
)
y=[]
for global_step in range(N):
    lr=lr_schedule(global_step)
    y.append(lr)
x=range(N)
plt.figure()
plt.plot(x,y,'r-')
plt.xlabel('步长')
plt.ylabel('学习率')
plt.title('分段衰减')
plt.show()

 

 

---

4.激活函数

激活函数的主要作用是提供网络的非线性建模能力。如果没有激活函数，那么该网络仅能够表达线性映射，此时即便有再多的隐藏层，其整个网络跟单层神经网络也是等价的。因此也可以认为，只有加入了激活函数之后，深度神经网络才具备了分层的非线性映射学习能力。

因为神经网络中每一层的输入输出都是一个线性求和的过程，下一层的输出只是承接了上一层输入函数的线性变换，所以如果没有激活函数，那么无论你构造的神经网络多么复杂，有多少层，最后的输出都是输入的线性组合，纯粹的线性组合并不能够解决更为复杂的问题。而引入激活函数之后，我们会发现常见的激活函数都是非线性的，因此也会给神经元引入非线性元素，使得神经网络可以逼近其他的任何非线性函数，这样可以使得神经网络应用到更多非线性模型中。

优秀的激活函数应满足：

• 非线性：激活函数非线性时，多层神经网络可逼近所有函数
• 可微性：优化器大多用梯度下降更新参数
• 单调性：当激活函数是单调的，能保证单层网络的损失函数是凸函数
• 近似恒等性：f（x）≈x 当参数初始为随机小值时，神经网络更稳定

激活函数输出值的范围：

• 激活函数输出值为有限值时，权重对特征的影响更显著，基于梯度的优化方法更稳定
• 激活函数输出值为无限值时，参数的初始值对模型的影响较大，建议调小学习率

  ---

常见激活函数：

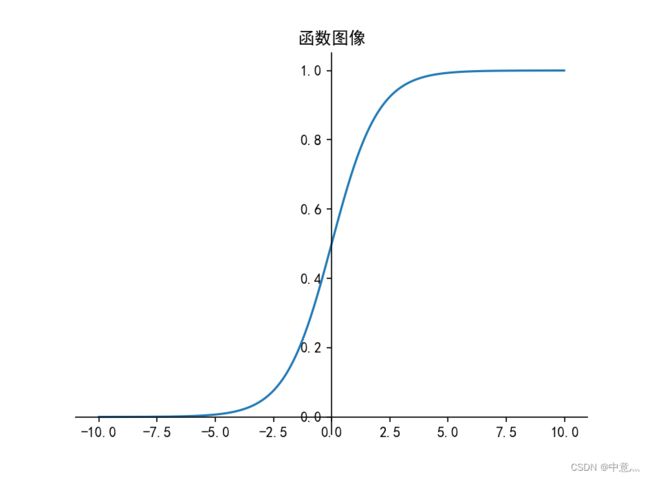
（1）sigmoid

                                                             

TensorFlow API:

tf.math.sigmoid(
    x, name=None
)

参数
x	张量类型为：float16float32float64complex64complex128
name	操作的名称（可选）。

 返回：与x类型相同的张量。

例： 

import tensorflow as tf
x=tf.constant([1.,2.,3.])
print(tf.math.sigmoid(x))

 tf.Tensor([0.7310586  0.8807971  0.95257413], shape=(3,), dtype=float32)

优点：

•  输出映射在（0，1）之间，单调连续，输出范围有限，优化稳定，可用作输出层
• 求导容易

缺点：

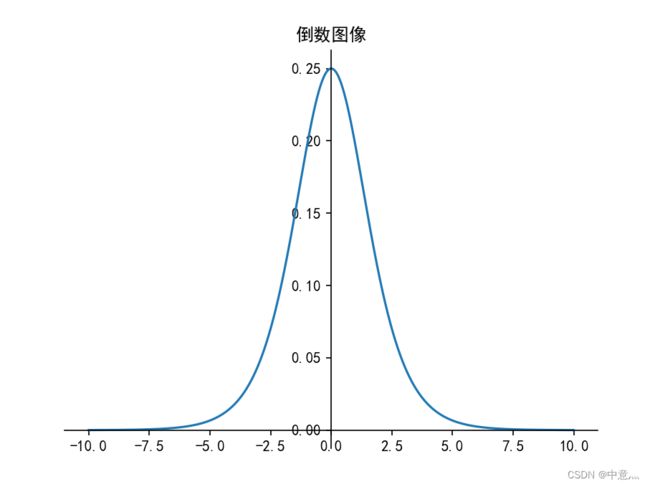
• 易造成梯度消失（在多层神经网络更新参数时，需要链式求导，多层倒数相乘趋近于0，会导致梯度消失）
• 输出非0均值，收敛慢
• 幂运算复杂，训练时间长

 sigmoid函数可应用在训练过程中。然而，当处理分类问题作出输出时，sigmoid却无能为力。简单来说，sigmoid函数只能处理两个类，不适用于多分类问题。而softmax（将其前向传播的输出值转化为概率分布）可以有效解决这个问题，并且softmax函数大都运用在神经网络中的最后一层网络中，使得置得区间在（0，1）之间，而不是二分类的。

---

（2）tanh

                                                             

 

 

 TensorFlow API:

tf.nn.relu(
    features, name=None
)

参数
features	必须是以下类型之一：Tensorfloat32float64int32uint8int16int8int64bfloat16uint16halfuint32uint64qint8
name	操作的名称（可选）

 例：

x=tf.constant([-float('inf'),-5,-0.5,1,1.5,4,float('inf')])#float('inf')返回一个无穷大的浮点数
print(tf.math.tanh(x))

tf.Tensor(
[-1.         -0.99990916 -0.46211717  0.7615942   0.9051482   0.9993292
  1.        ], shape=(7,), dtype=float32) 

优点：

• 1.比sigmoid函数收敛速度更快
• 2.相比sigmoid函数，其输出以0为中心

缺点：

• 1.易造成梯度消失
• 2.幂运算复杂，训练时间长 

  ---

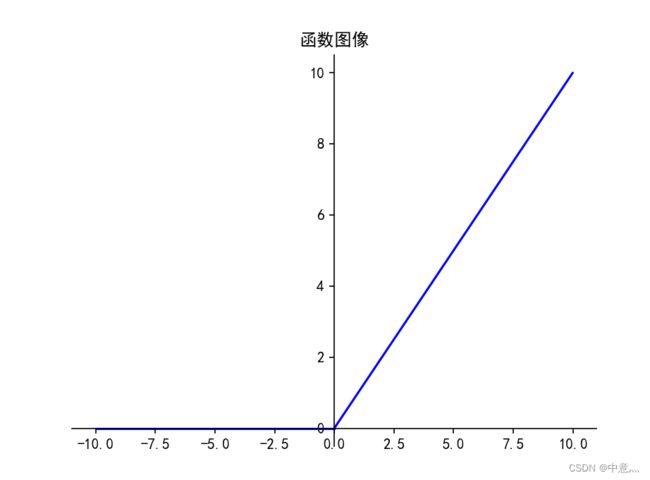
（3）ReLU

                                   

 TensorFlow API：

tf.keras.activations.relu(
    x, alpha=0.0, max_value=None, threshold=0.0
)

参数
x	输入 或 tensorvariable
alpha	控制低于阈值的值的斜率的张量。float
max_value	设置饱和阈值（函数将返回的最大值）的张量。float
threshold	给出激活函数的阈值，低于该值的值将被阻尼或设置为零。float

例： 

foo = tf.constant([-10, -5, 0.0, 5, 10], dtype = tf.float32)
print(tf.keras.activations.relu(foo))
print(tf.keras.activations.relu(foo, alpha=0.5))
print(tf.keras.activations.relu(foo, max_value=5.))
print(tf.keras.activations.relu(foo, threshold=5.))

 tf.Tensor([ 0.  0.  0.  5. 10.], shape=(5,), dtype=float32)
tf.Tensor([-5.  -2.5  0.   5.  10. ], shape=(5,), dtype=float32)
tf.Tensor([0. 0. 0. 5. 5.], shape=(5,), dtype=float32)
tf.Tensor([-0. -0.  0.  0. 10.], shape=(5,), dtype=float32)

优点：

• 1.解决了梯度消失问题（在正区间）
• 2.只需判断输入是否大于0，计算速度快
• 3.收敛速度远快于sigmoid和tanh，因为不涉及幂运算 
• 4.提供了神经网络的稀疏表达能力

缺点：

• 1.输出非0均值，收敛慢
• 2.Dead ReLU问题：某些神经元可能永远不回被激活，导致相应的参数永远不能被更新。（即送入激活函数的输入特征是负数时，激活函数输出为0，反向传播的梯度也是0，导致参数无法更新，造成神经元死亡，此时应当避免过多的负数特征进入）

  ---

（4）Leaky ReLU

                                                          

 

 TensorFlow API:

tf.nn.leaky_relu(
    features, alpha=0.2, name=None
)

参数
features	表示预激活值的 张量。必须是以下类型之一：Tensorfloat16float32float64int32int64
alpha	激活函数在 x 处的斜率< 0。
name	操作的名称（可选）。

 理论上来讲，Leaky ReLU有ReLU的所有优点，外加不回有Dead ReLU问题，但在实际操作中，并没有完全证明Leaky ReLU总是好于ReLU

例： 

x=tf.constant([-3.,0.,-0.,3.])
print(tf.nn.leaky_relu(x))

 tf.Tensor([-0.6  0.  -0.   3. ], shape=(4,), dtype=float32)

---

 

（5）softmax

                                           

TensorFLow API：

tf.nn.softmax(
    logits, axis=None, name=None
)

参数
logits	非空 .必须是以下类型之一：Tensorhalffloat32float64
axis	将执行尺寸 softmax。默认值为 -1，表示最后一个维度。
name	操作的名称（可选）。

 对神经网络全连接层输出进行变换，使其服从概率分布，即每个值抖位于[0,1]区间且和为1

 例：

x=tf.constant([3.,5.,1.])
print(tf.nn.softmax(x))

 tf.Tensor([0.11731042 0.8668133  0.01587624], shape=(3,), dtype=float32)

---

 

（6）建议

对于初学者的建议：

• 1.首选ReLU激活函数
• 2.学习率设置较小值
• 3.输入特征标准化，即让输入特征满足以0为均值，1为标准差的正太分布
• 4.初始化问题：初始参数中心化，即让随机生成的参数满足以0为均值，（2/当前层输入特征个数）^1/2为标准差的正态分布

---

 

5.损失函数

损失函数（loss function）就是用来度量模型的预测值f(x)与真实值Y的差异程度的运算函数，它是一个非负实值函数，通常使用L(Y, f(x))来表示，损失函数越小，模型的鲁棒性就越好。

损失函数使用主要是在模型的训练阶段，每个批次的训练数据送入模型后，通过前向传播输出预测值，然后损失函数会计算出预测值和真实值之间的差异值，也就是损失值。得到损失值之后，模型通过反向传播去更新各个参数，来降低真实值与预测值之间的损失，使得模型生成的预测值往真实值方向靠拢，从而达到学习的目的，即损失函数为模型优化指明方向。

（1）均方误差损失函数

均方误差（Mean Square Error）是回归问题最常用的损失函数。回归问题解决的是对具体数值的预测，比如房价预测、销量预测等。这些问题需要预测的不是一个事先定义好的类别，而是一个任意实数。均方误差定义如下：

                                                 

 其中为一个batch中第i个数据的真实值，而为模型的预测值。

TensorFlow API：

tf.keras.losses.MeanSquaredError(
    reduction=losses_utils.ReductionV2.AUTO,
    name='mean_squared_error'
)

功能：计算均方误差 

例：

import tensorflow as tf
y_true=tf.constant([0.2,0.7])
y_pred=tf.constant([0.4,0.5])
MSN=tf.keras.losses.MeanSquaredError()
print(MSN(y_true,y_pred))

 tf.Tensor(0.04, shape=(), dtype=float32)

---

 

（2）交叉熵损失函数

交叉熵（Cross Entropy）表征两个概率分布之间的距离，交叉熵越小说明二者分布越接近，是分类问题中使用较广泛的损失函数。

                                                   

其中y_代表数据的真实值，y表示神经网络的预测值。

如一直一个分类问题真实值为（0，1），预测值为y1=(0.6,0.4) y2=(0.8,0.2)

算的H1=0.511，H2=0.223,由于H2

对于多分类问题， 神经网络的输出一般不是概率分布，因此需要引入softmax层，使其输出服从概率分布。TensorFlow中可计算交叉熵损失函数的API有：

tf.keras.losses.CategoricalCrossentropy

tf.keras.losses.CategoricalCrossentropy(
    from_logits=False,
    label_smoothing=0.0,
    axis=-1,
    reduction=losses_utils.ReductionV2.AUTO,
    name='categorical_crossentropy'
)

功能：计算交叉熵 

参数
from_logits	是否应为对数张量。默认情况下，我们假设 对概率分布进行编码。y_predy_pred
label_smoothing	浮点数在 [0， 1] 中。当> 0 时，将平滑标签值，这意味着标签值的置信度将放宽。例如，if ，用于非目标标签和目标标签。0.10.1 / num_classes0.9 + 0.1 / num_classes
axis	计算交叉熵的轴（要素轴）。默认值为 -1。
reduction	tf.keras.loss.reduction 的 type to apply to loss.缺省值为 。 表示缩减选项将由使用上下文确定。对于几乎所有情况，这默认为 。当与 tf.distribut.Strategy 一起使用时，在内置训练循环（如 tf.keras 和 ）之外，使用 或 将引发错误。有关更多详细信息，请参阅此自定义培训教程。AUTOAUTOSUM_OVER_BATCH_SIZEcompilefitAUTOSUM_OVER_BATCH_SIZE
name	实例的可选名称。默认值为“categorical_crossentropy”。

例： 

y_true=tf.constant([1,0,0])
y_pred1=tf.constant([0.5,0.4,0.1])
y_pred2=tf.constant([0.8,0.1,0.1])
cce=tf.keras.losses.CategoricalCrossentropy()
print(cce(y_true,y_pred1))
print(cce(y_true,y_pred2))

tf.Tensor(0.6931472, shape=(), dtype=float32)
tf.Tensor(0.22314353, shape=(), dtype=float32) 

 tf.nn.softmax_cross_entropy_with_logits

tf.nn.softmax_cross_entropy_with_logits(
    labels, logits, axis=-1, name=None
)

功能：logits经过softmax归一化后，与labels进行交叉熵计算。

在机器学习中，对于多分类问题，把未经过softmax归一化的向量值称为logits。logits经过softmax层后，输出服从概率分布的向量。 

参数
labels	在类别这一维度上，每个向量应服从有效的概率分布，例如，在labels的shape为[batch_size, num_classes]的情况下labels[i]应服从概率分布
logits	每个类别的激活值，通常是线性输出。激活值需要经过softmax归一化
axis	类维度。默认值为 -1，即最后一个维度。
name	操作的名称（可选）。

 返回：交叉熵损失值

例：

logits = [[4.0, 2.0, 1.0], [0.0, 5.0, 1.0]]
labels = [[1.0, 0.0, 0.0], [0.0, 0.8, 0.2]]
print(tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits))

tf.Tensor([0.16984604 0.82474494], shape=(2,), dtype=float32) 

 tf.nn.sparse_softmax_cross_entropy_with_logits

tf.nn.sparse_softmax_cross_entropy_with_logits(
    labels, logits, name=None
)

功能：labels经过one-hot编码（独热编码），logits经过softmax归一化，两者进行交叉熵计算，通常labels的shape为[batch_size]，logits的shape为[batch_size，num_classes]。sparse可理解为对labels进行稀疏化处理（即进行one-hot编码） 

参数
labels	标签的索引值
logits	每个类别的激活值，通常为线性输出。激活值需要经过softmax归一化。
name	操作的名称（可选）。

返回：交叉熵损失值 

logits = tf.constant([[2., -5., .5, -.1],
                      [0., 0., 1.9, 1.4],
                      [-100., 100., -100., -100.]])
labels = tf.constant([0, 3, 1])
print(tf.nn.sparse_softmax_cross_entropy_with_logits(
    labels=labels, logits=logits))

tf.Tensor([0.29750752 1.1448325  0.        ], shape=(3,), dtype=float32) 

---

 

（3）自定义损失函数

根据具体任务和目的，设计不同的损失函数 。

---

 

6.欠拟合与过拟合

欠拟合的解决办法：

• 增加输入特征项
• 增加网络参数
• 减少正则化参数

过拟合解决方法：

• 数据清洗，进行归一化处理
• 增大训练集
• 采用正则化
• 增大正则化参数

---

 

7.优化器 

优化算法可以分成一阶优化和二阶优化算法，其中一阶优化就是指的梯度算法及其变种，而二阶优化一般是用二阶导数（Hessian）来计算，如牛顿法，由于需要计算Hessian阵和其逆矩阵，计算量较大，因此没有流行开来。这里主要总结一下一阶优化的各种梯度下降方法：

深度学习优化算法经历了SGD->SGDM->NAG->AdaGrad->AdaDelta->Adam->Nadam这样的发展历程。

定义：待优化参数，损失函数 ，初始学习率，每次迭代一个batch，t表示当前batch迭代的总次数。

• 1.计算损失函数关于当前参数的梯度：
• 2.根据历史梯度计算一阶动量和二阶动量：,
• 3.计算当前时刻的下降梯度：
• 4.根据下降t梯度进行更新：

步骤3，4对于各个算法都是一致的，主要差别体现在步骤1和2上。

常见优化器API：

• tf.keras.optimizers.SGD
• tf.keras.optimizers.Adagrad
• tf.keras.optimizers.RMSprop
• tf.keras.optimizers.Adadelta
• tf.keras.optimizers.Adam 

优化器选择：

没有优化器能做到再任何情况下都表现良好，根据具体任务选择合适的优化器即可。如一些优化器在计算机视觉任务表现良好，另一些在涉及RNN网络时表现良好，甚至在稀疏数据情况下表现更出色。

初学者，优先考虑Adam或者SGD+Neterov Momentum，具体关于优化器的解释，大家自行去了解。