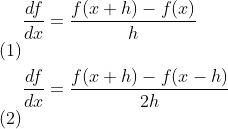CS231n-2022 Module1: 神经网络3：Learning之梯度检查

目录

1. 前言

2. 使用中心对称方程式（centered formula）

3. 使用相对误差进行比较

4. 使用双精度

5. Stick around active range of floating point

6. Kinks in the objective

7. 只是用少量数据点

8. Be careful with the step size h

9. Gradcheck during a “characteristic” mode of operation.

10. 不要让正则化损失淹没了数据损失

11. 记住关掉dropout和数据增强（augmentations）

12. Check only few dimensions

---

1. 前言

        本文编译自斯坦福大学的CS231n课程（2022） Module1课程中神经网络部分之一，原课件网页参见：

CS231n Convolutional Neural Networks for Visual Recognitionhttps://cs231n.github.io/neural-networks-3/        本文（本系列）不是对原始课件网页内容的完全翻译，只是作为学习笔记的摘要总结，主要是自我参考，而且也可能夹带一些私货（自己的理解和延申，不保证准确性）。如果想要了解更具体的细节，还请服用原文。如果本摘要恰巧也对小伙伴们有所参考则纯属无心插柳概不认账^-^。      

        前面两篇：

        CS231n-2022 Module1: 神经网络概要1：Setting Up the Architecture   

        CS231n-2022 Module1: 神经网络概要2 

        前面章节介绍了网络的静态部分：网络连接、数据、损失函数等。接下来将讨论动态（Dynamics）部分，关于如何进行（参数）学习（换言之，如何训练）以及如何找到超参数，如何进行网络性能评估。 

        本篇介绍学习（训练）中的一个重要环节：梯度检查。梯度检查是编写神经网络代码和调试的重要环节，通过对比梯度分析结果与实际的数值计算结果来进行的代码的sanity check。这里介绍一些相关的小贴士、小技巧以及需要注意的事项。

2. 使用中心对称方程式（centered formula）

                

        其中h通常为一个很小的值（比如说1e-5）。记住，要使用式（2）这样的中心对称表达式，而不是式（1）。式（2）的估计误差会远远地小于式（1）。利用泰勒展开，可以很容易地证明式（1）的误差为，而式（2）的误差为（换句话说，它是二阶近似）。

3. 使用相对误差进行比较

        简而言之，要使用如下所示的相对误差：

                

        而不是简单的绝对误差。

        后者为什么不行是因为，比如说，对于很大的量比如说1e3级别的值，1e-4的误差是很小的；但是对于本身只有1e-4大小的量，1e-4的误差就可以说是巨大的了。采用相对误差可以避免这种问题。

        多大的（相对）误差算大呢，以下是一些经验性的法则:

• relative error > 1e-2 通常意味梯度计算有错误
• 1e-2 > relative error > 1e-4 应该让你感到警觉可能哪里不对劲
• 1e-4 量级的 relative error 对于存在kinks(扭结)的目标函数来说大致算合理，但是对于不存在kinks的情况（比如说使用tanh或者sigmoid）1e-4的相对误差通常意味着太高了
• 小于等于1e-7的相对误差，通常你应该感到安心

        神经网络越深，相对误差相应地会变大。所以，对于比如说10层的神经网络，1e-2量级的相对误差或许就算可以的了，毕竟误差是逐层累积的。

4. 使用双精度

        虽然可能有点违反直觉，使用单精度浮点数进行梯度检查的话，即便梯度实现正确也可能会得到很大的相对误差。根据我（原作者）的经验，甚至有可能仅仅从单精度浮点数切换到双精度浮点数，就可能导致相对误差从1e-2直接降到1e-8量级。

5. Stick around active range of floating point

        关于浮点运算，读一读以下这篇经典文章会让你受益匪浅： “What Every Computer Scientist Should Know About Floating-Point Arithmetic”

        通常来说，对非常小的数进行运算或者比较更容易遭遇数值问题（numerical issues）。如果原始的梯度值已经很小的话，可以临时把它们放大到一个更“好”的浮点数的区间（比如说1附近的区间），再进行处理是一个明智的避免数值问题陷阱的做法。

6. Kinks in the objective

        梯度检查的准确性问题的原因之一来自于kinks，kinks是指目标函数（objective function）的不可微部分，比如说ReLU、SVM loss, Maxout neurons, etc. 以ReLU为例，在x<0区间梯度显然为0，但是在比如说处进行梯度检查，when h>1e-6, ，将会得到一个非零的梯度数值结果，这样将导致梯度检查出现错误的结果。这是一种相当普遍的情况。

        Note that it is possible to know if a kink was crossed in the evaluation of the loss. This can be done by keeping track of the identities of all “winners” in a function of form ; That is, was x or y higher during the forward pass. If the identity of at least one winner changes when evaluating f(x+h) and then f(x−h), then a kink was crossed and the numerical gradient will not be exact.

7. 只是用少量数据点

        对于含有kinks（ e.g. due to use of ReLUs or margin losses etc.）的损失函数，使用的数据点越少（即训练用数据集越小）的话，其中包含的kinks也相应越少。因此，使用一个很小的数据集，在进行梯度检查的近似数值计算时恰好跨越某个kink的概率就会变得很小，但是却并不影响梯度检查的有效性，即在小数据集时能通过梯度检查的话，几乎可以确定在完整数据集上也能通过梯度检查。而且，使用小数据集还使得梯度检查更快速高效。

8. Be careful with the step size h

        步长h不是越小越好，因为如前所述，用太小的数进行运算容易遭遇数值问题。1e-6 左右是一个大致合理的选择。更多的信息请参考http://en.wikipedia.org/wiki/Numerical_differentiation，其中有一个关于h vs numerical gradient error 的图：

       Example showing the difficulty of choosing due to both rounding error and formula error 

9. 在典型动作模式下进行梯度检查

        一个重要的事情是，梯度检查仅仅是针对参数空间中的某个特定的（通常是随机的）点进行，即便在这个特定的点的梯度检查结果正常，并不能保证梯度实现的全局正确性。此外，随机初始化可能并不是参数空间中最有代表性的点（the most “characteristic” point），甚至实际上可能导入病态的情况（pathological situations）：梯度看似正确实现了（即通过了梯度检查）但是事实上不是。 比如说，SVM在非常小的权重参数初始化条件下，会给所有的数据点打几乎为零的分数，而梯度则在所有数据点上呈现一种特殊的模式。An incorrect implementation of the gradient could still produce this pattern and not generalize to a more characteristic mode of operation where some scores are larger than others. 因此，为了安全起见，最好给定一个很短的burn-in的时间，即让神经网络运行学习一段时间，并在损失函数开始下降时再进行梯度检查。在第一次迭代中就做梯度检查的危险在于可能遭遇病态的边缘情况（pathological edge cases）并掩盖梯度的错误实现。

10. 不要让正则化损失淹没了数据损失

        损失函数通常由正则化损失和数据损失两部分构成。如果正则化loss（通常其梯度表达式相对比较简单因而不容易出错）较大而淹没了数据loss的话，很可能在梯度检查中掩盖了数据loss部分的错误。因此建议先关掉正则化先单独对数据loss进行梯度检查，然后再对正则化loss进行检查。再进行第二步的正则化loss的检查时可以通过增加正则化强度以凸显正则化loss的作用，这样就能（在数据loss存在的前提下）更容易检查出正则化loss的梯度实现中的错误。

11. 记住关掉dropout和数据增强（augmentations）

        当执行梯度检查时，记住关闭神经网络中任何不确定因素(non-deterministic effects)，比如说，dropout, random data augmentations等等。否则的话它们可能会在计算数值梯度时导入巨大的误差。当然，关闭了它们也就意味着在梯度检查中无法覆盖对它们的检查 (e.g. it might be that dropout isn’t backpropagated correctly)。因此，一个较好的折衷是在固定的随机种子条件下进行评估。

12. Check only few dimensions

In practice the gradients can have sizes of million parameters. In these cases it is only practical to check some of the dimensions of the gradient and assume that the others are correct. Be careful: One issue to be careful with is to make sure to gradient check a few dimensions for every separate parameter. In some applications, people combine the parameters into a single large parameter vector for convenience. In these cases, for example, the biases could only take up a tiny number of parameters from the whole vector, so it is important to not sample at random but to take this into account and check that all parameters receive the correct gradients.