【论文阅读笔记】Structured-light 3D surface imaging: a tutorial(结构光三维表面成像)
Geng J. Structured-light 3D surface imaging: a tutorial[J]. Advances in Optics and Photonics, 2011, 3(2): 128-160.
(截止2022/3/20日该文被被引用1460次)
该文回顾了3D表面成像技术的进展,重点介绍了基于结构光的非接触式3D表面测量技术、数字光投影技术提供的高速和高分辨率模式投影能力,以及成像传感器技术,可使新一代3D表面测量应用系统在速度、精度、分辨率、模块化和易用性方面比现有系统提供更好的功能和性能。讨论了三维成像系统的性能指标,并对各种三维表面成像方案进行了分类、说明和比较。还讨论了校准技术,因为它们在实现所需精度方面起着关键作用。通过几个例子讨论了三维表面成像技术的许多应用。
1. Introduction
世界是三维的,传统的相机和成像传感器只能获取缺乏深度信息的二维(2D)图像,限制了我们感知和理解现实世界的能力。在过去几十年中,高分辨率和高速电子成像传感器的进步以及不断增长的计算能力的推动下,3D表面成像技术的研究取得了巨大进展。在这篇文章中,概述了结构光三维成像技术的最新进展。
“3D成像”指能够获取真实3D数据的技术,即3D对象某些属性的值,例如密度分布,3D坐标(x,y,z),医学成像领域的计算机断层扫描CT和磁共振成像(MRI)等等。
相比之下,表面成像处理物体表面上的点的(x,y,z)坐标的测量。因为表面通常是非平面的,所以它是在三维空间中描述的,成像问题称为三维表面成像。测量结果可视为深度(或范围)z随位置变化的地图,它可以用数字矩阵形式 z i j = ( x i , y i , ) , i = 1 , 2 , . . . , L , j = 1 , 2 , . . . , M {z_ij=(x_i,y_i,),i=1,2,...,L,j=1,2,...,M} zij=(xi,yi,),i=1,2,...,L,j=1,2,...,M表示。 该过程也被称为3D表面测量、测距、距离传感、深度映射、表面扫描等。这些术语用于不同的应用领域,通常指大致等效的基本表面成像功能,仅在系统设计、实施和/或数据格式的细节上有所不同。
更通用的3D表面成像系统能够获取与非平面表面上的每个点相关联的标量值,例如表面反射率。如点云 P i = ( x i , y i , z i , f i ) , i = 1 , 2 , . . . , N {P_i=(x_i,y_i,z_i,f_i),i=1,2,...,N} Pi=(xi,yi,zi,fi),i=1,2,...,N,其中 f i f_i fi表示数据集中第 i i i个曲面点的值。同样地,彩色表面图像用 P i = ( x i , y i , z i , r i , g i , b i ) , i = 1 , 2 , . . . , N {P_i=(x_i,y_i,z_i,r_i,g_i,b_i),i=1,2,...,N} Pi=(xi,yi,zi,ri,gi,bi),i=1,2,...,N表示,其中向量 ( r i , g i , b i ) {(r_i,g_i,b_i)} (ri,gi,bi)表示与第 i i i个表面点关联的红色、绿色和蓝色部分。光谱表面特性也可以用更大维度的向量来描述。
3D表面成像的一种主要方法是基于结构光,如图1所示,空间变化的2D结构照明由特殊的投影仪或空间光调制器调制的光源产生。结构光图案上每个像素的强度由数字信号 I i j = ( i , j ) , i = 1 , 2 , . . . I , j = 1 , 2 , . . . , J {I_ij=(i,j),i=1,2,...I,j=1,2,...,J} Iij=(i,j),i=1,2,...I,j=1,2,...,J,其中 ( i , j ) {(i,j)} (i,j)表示投影图案的(x,y)坐标。本文讨论的结构光投影图案是2D图案。
成像传感器(例如摄像机)用于在结构光照明下获取场景的2D图像。如果场景是没有任何3D表面变化的平面,则获取的图像中显示的图案与投影的结构光图案相似。但是,当场景中的曲面是非平面的时,曲面的几何形状会扭曲从摄影机看到的投影结构光图案。结构光三维表面成像技术的原理是根据投影结构光图案的畸变信息提取三维表面形状。通过使用各种结构光原理和算法,可以计算场景中物体的精确三维表面轮廓。
如下图所示,成像传感器、结构光投影仪和物体表面点之间的几何关系可以通过三角测量原理表示为: R = B s i n ( θ ) s i n ( α + θ ) {R=B{sin(θ) \over{sin(α+θ)}}} R=Bsin(α+θ)sin(θ)
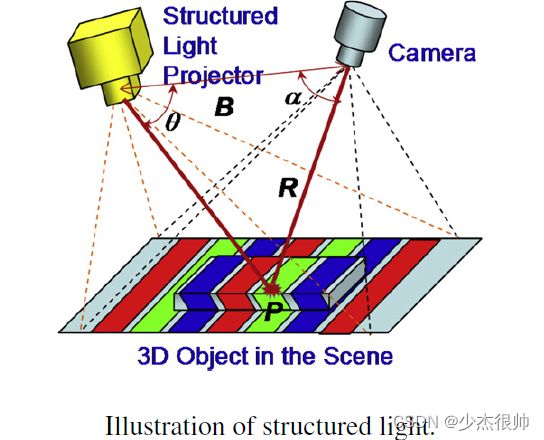
基于三角剖分的三维成像的关键是在二维投影模式下将单个投影光斑与采集的图像区分开来的技术。为此提出了各种方案,本问将概述基于结构光照明的各种方法。
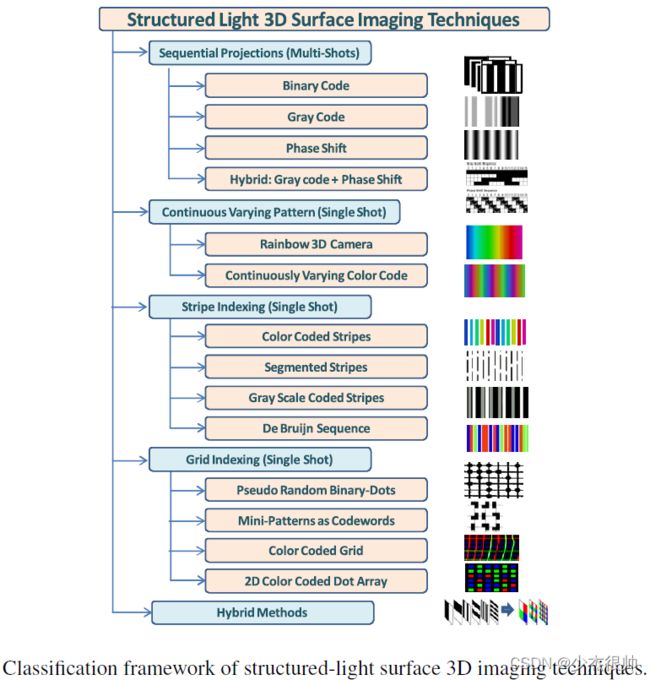
目前有许多利用结构光进行表面成像的技术。在本综述中,我们首先将所有技术分为顺序(多个镜头)和单镜头类别,如下图所示。如果目标3D目标是静态的,且应用程序没有对采集时间施加严格限制,则可以使用多镜头技术,通常可能会产生更可靠、更准确的结果。然而,如果目标正在移动,则必须使用单次拍摄技术来获取特定时刻3D对象的快照3D表面图像。我们进一步将单镜头技术分为三大类:使用连续变化的结构光模式的技术、使用一维编码方案的技术(条带索引)和使用二维编码方案的技术(网格索引)。每种技术都有自己的优缺点,具体取决于具体的应用。
2. Sequential Projection Techniques
2.1 Binary Patterns and Gray Coding
二进制编码使用黑白条纹形成一系列投影图案,这样物体表面上的每个点都拥有一个独特的二进制代码。N个图案可以编码 2 N {2^N} 2N个条纹。下图显示了一个简化的5位投影图,将这一系列图案投影到静态场景上,就有32( = 2 5 {=2^5} =25)个用唯一条纹编码的唯一区域。三维坐标。三维坐标(x,y,z)可以计算(基于三角测量原理)沿每条水平线的所有32个点,从而形成3D图像的完整框架
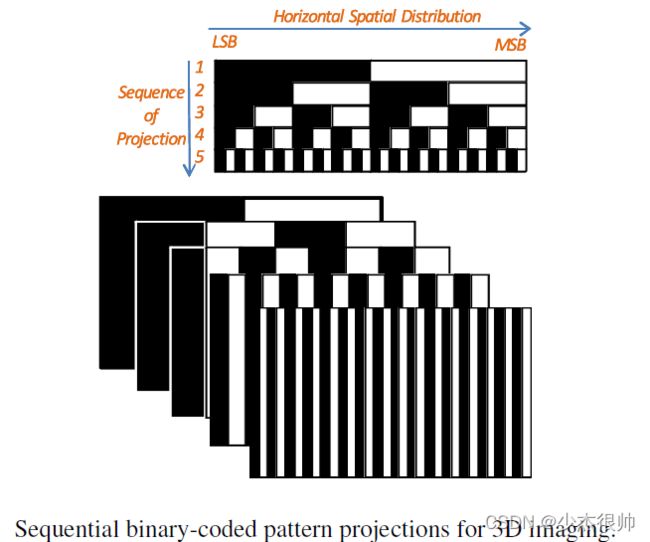
二进制编码技术非常可靠,而且对表面特征不太敏感,因为所有像素中只存在二进制值。然而,为了获得高的空间分辨率,需要投影大量的序列图案,场景中的所有对象都必须保持静止。3D图像采集的整个持续时间可能比实际3D应用程序允许的时间更长。
2.2 Gray-Level Patterns
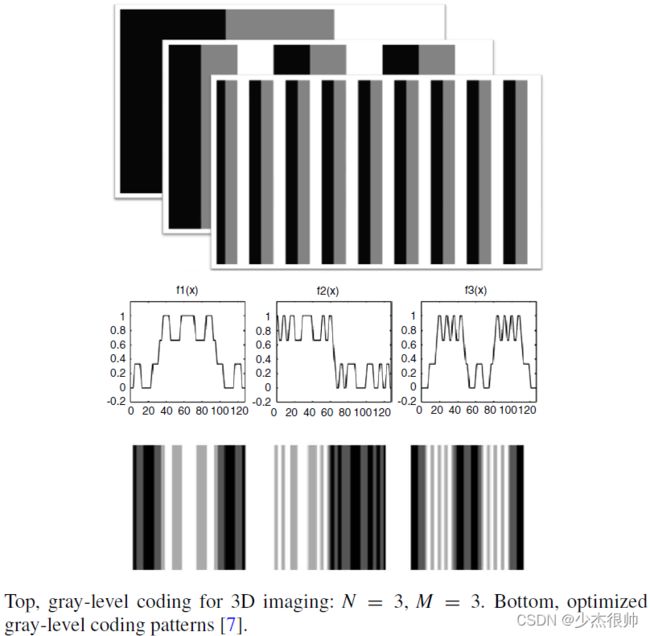
为了有效减少获得高分辨率3D图像所需的图案数量,开发了灰度图案。例如,可以使用M个不同的强度级别(而不是二进制代码中只有两个)来生成投影图案的独特编码。在这种情况下,N个图案可以编码 M N {M^N} MN条带。每个条带的代码都可以可视化为基于N的空间中的一个点,每个维度有M个不同的值。例如,如果N=3,M=4,那么代码条纹的总数是64(= 4 3 4^3 43)。相比之下,对于二进制代码的64个条纹,需要6个图案。在设计二进制和灰色编码图案时存在优化。目标是在所有唯一的码字中最大化某种类型的距离度量。对于实际的3D成像应用,能够区分相邻条纹非常重要。下图显示了在希尔伯特空间中优化的灰度编码模式示例。
2.3. Phase Shift
相移是一种众所周知的三维表面成像条纹投影方法。一组正弦图案投影到物体表面(如下图)。三个投影条纹图中每个像素(x,y)的强度表示为:
I 1 ( x , y ) = I 0 ( x , y ) + I m o d ( x , y ) c o s ( Φ ( x , y ) − θ ) {I_1(x,y)=I_0(x,y)+I_{mod}(x,y)cos(Φ(x,y)-θ)} I1(x,y)=I0(x,y)+Imod(x,y)cos(Φ(x,y)−θ)
I 2 ( x , y ) = I 0 ( x , y ) + I m o d ( x , y ) c o s ( Φ ( x , y ) ) {I_2(x,y)=I_0(x,y)+I_{mod}(x,y)cos(Φ(x,y))} I2(x,y)=I0(x,y)+Imod(x,y)cos(Φ(x,y))
I 3 ( x , y ) = I 0 ( x , y ) + I m o d ( x , y ) c o s ( Φ ( x , y ) + θ ) {I_3(x,y)=I_0(x,y)+I_{mod}(x,y)cos(Φ(x,y)+θ)} I3(x,y)=I0(x,y)+Imod(x,y)cos(Φ(x,y)+θ)
其中 I 1 ( x , y ) I_1(x,y) I1(x,y), I 2 ( x , y ) I_2(x,y) I2(x,y), I 3 ( x , y ) I_3(x,y) I3(x,y)是三种条纹图案的强度, I 0 ( x , y ) I_0(x,y) I0(x,y)是直流分量(背景), I m o d ( x , y ) I_{mod}(x,y) Imod(x,y)是调制信号振幅。Φ(x,y)是相位,θ是恒定相移角。
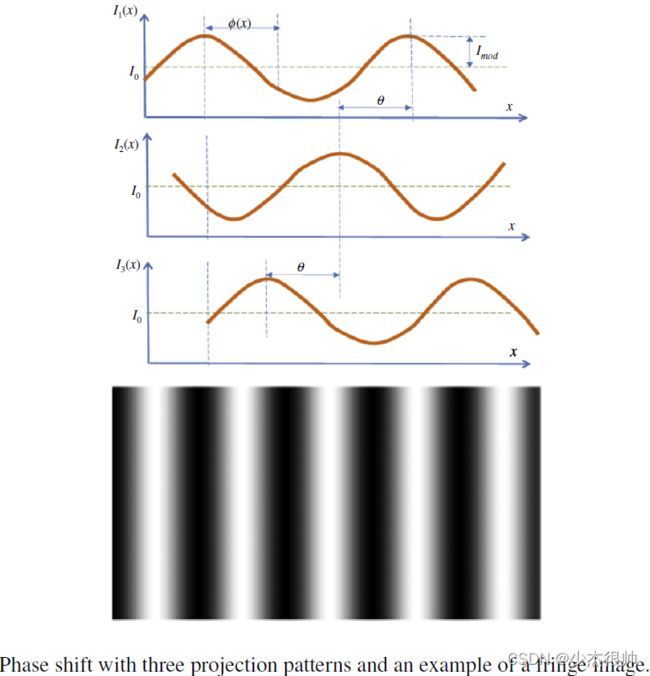
相位解包裹是将包裹相位转换为绝对相位的过程。相位信息Φ(x,y)可以从三个条纹图案中的强度中得到(即展开):
Φ ′ = a r c t a n [ 3 I 1 ( x , y ) − I 3 ( x , y ) 2 I 2 ( x , y ) − I 1 ( x , y ) − I 3 ( x , y ) ] { Φ'=arctan[\sqrt{3} \frac{I_1(x,y)- I_3(x,y)}{2I_2(x,y)-I_1(x,y)- I_3(x,y)} ]} Φ′=arctan[32I2(x,y)−I1(x,y)−I3(x,y)I1(x,y)−I3(x,y)]
可以通过在Φ’(x,y)上加上或减去2π的倍数来消除2π处反正切函数的不连续性:(如下图)

Φ ( x , y ) = Φ ′ ( x , y ) + 2 k π {Φ(x,y)=Φ'(x,y)+2kπ} Φ(x,y)=Φ′(x,y)+2kπ
其中k是表示投影周期的整数。请注意,展开方法仅提供相对展开,不求解绝对相位。3D坐标(x,y,z)可根据测量相位和参考平面相位之间的差异计算。如下图所示:
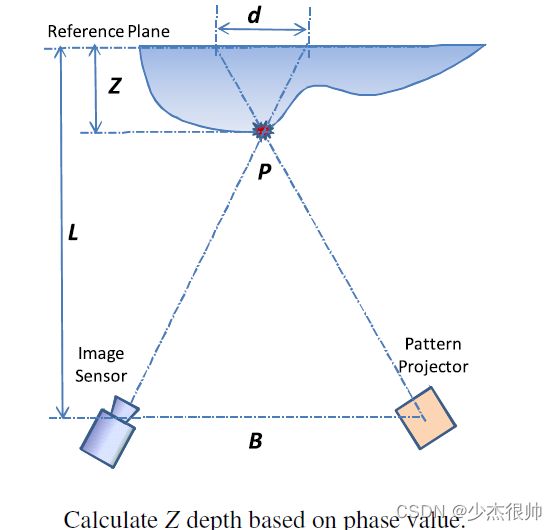
Z L − Z = d B o r Z = L − Z B d {\frac{Z}{L-Z}=\frac{d}{B} or Z=\frac{L-Z}{B}d} L−ZZ=BdorZ=BL−Zd
可得深度信息Z:
Z = L B d ≈ L B ( Φ − Φ 0 ) { Z=\frac{L}{B}d\approx\frac{L}{B}(Φ-Φ_0)} Z=BLd≈BL(Φ−Φ0)
2.4. Hybrid Method: Phase Shift C Gray Coding
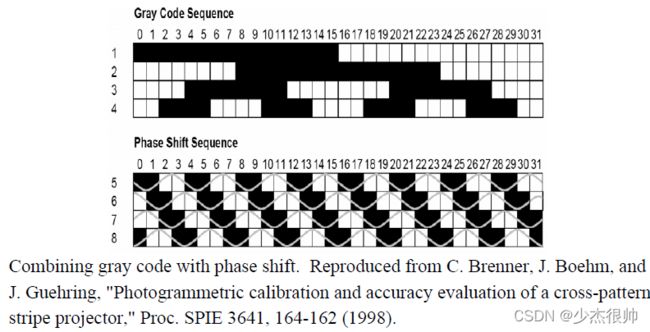
正2.3小节中所讨论的,相移技术有两个主要问题:展开方法只提供相对展开,而不解决绝对相位。如果两个曲面的不连续性大于2 π,则基于解包裹的任何方法都无法正确地相对于彼此展开这两个曲面。这些问题通常被称为“模糊”,可以通过结合使用格雷码投影和相移技术来解决。下图显示了在32条带编码序列中将格雷码投影与相移相结合的示例。格雷码在没有任何模糊性的情况下确定相位的绝对范围,而相移提供的亚像素分辨率超过了格雷码提供的条纹数。然而,混合方法需要更多的投影,并且不适合动态对象的三维成像。
2.5. Photometrics
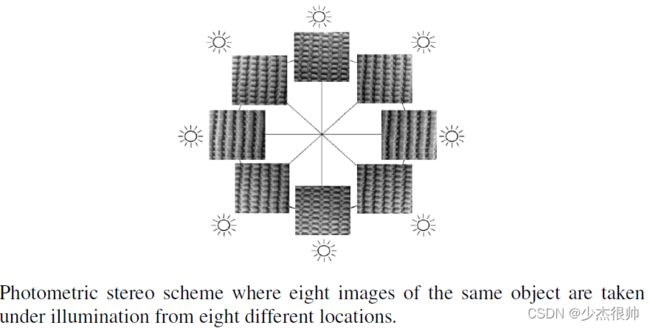
Woodham首创的光度立体视觉法是一种从明暗处理到形状的变体方法。它通过使用从同一视点但在不同方向照明下拍摄的同一表面的一系列图像来估计局部表面方向(如下图)。因此,它通过使用多幅图像解决了形状不适定问题。光度立体要求所有光源都是点光源,并且只估计局部曲面方向(梯度)。它假设3D曲面连续,并需要一个“起点”(对象曲面上的一个点,其(x,y,z)坐标已知)来进行3D重建算法。
3. Full-Frame Spatially Varying Color Pattern
顺序投影技术的主要缺点包括无法获取动态运动中的3D对象或活体对象(如人体部位)。现在,我们介绍了几种单镜头3D表面成像技术,这些技术利用了投影图案中的颜色信息或独特的编码方案,只需要在颜色图案照明下获取一幅物体的图像,就可以获得3D图像的完整场景中每个可见点的坐标(x,y,z)。
3.1. Rainbow 3D Camera
下图展示了彩虹3D相机的基本概念。
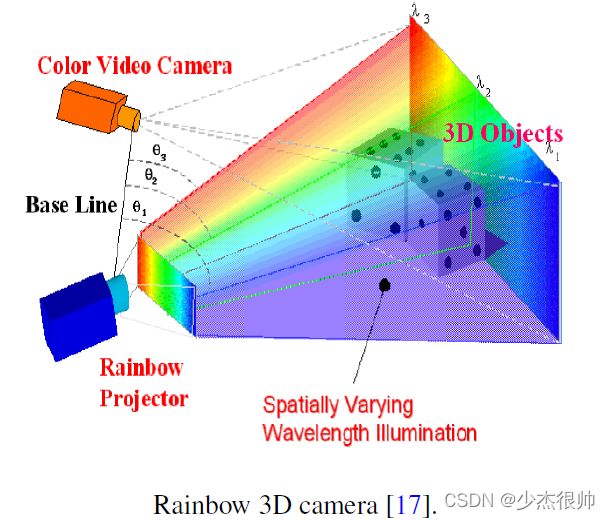
与传统的立体相机不同,彩虹3D相机必须从一对立体图像中提取相应的特征来计算深度值,它将空间变化的波长照明投射到物体表面。彩虹光投影仪的固定几何结构在光平面的投影角θ和特定光谱波长λ之间建立了一对一的对应关系,从而在每个表面点上提供了易于识别的标识点。在已知基线B和已知视角α的情况下,可以使用简单的三角剖分原理计算对应于每个单独像素的3D范围值,并且可以以相机的帧速率(30帧/秒或更快)在单个快照中获得3D范围图像的完整帧。
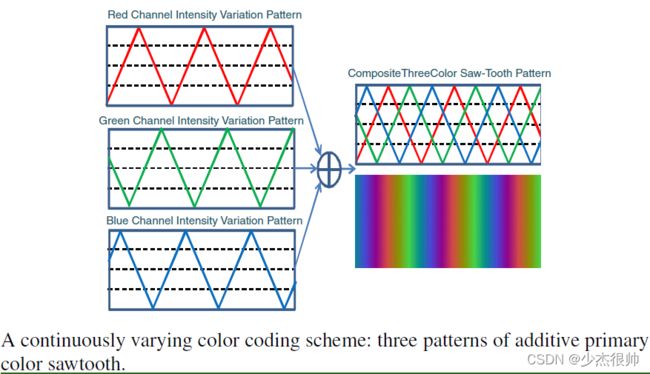
3.2. Continuously Varying Color Coding
组成各种连续变化的颜色图案来编码空间位置信息是可以的。例如,我们可以为投影仪的每个颜色通道构造一个强度变化模式,这样,当这些模式加在一起时,各个颜色通道中的这些模式就会形成一个连续变化的颜色模式。如下图显示了三个附加原色通道的强度变化模式示例。当它们加在一起时,就会形成彩虹状的彩色投影图案。请注意,这种类型的颜色图案不一定遵循颜色光谱(波长)的线性变化关系。然而,由于来自每个颜色通道的贡献之间的比率是已知的,因此解码方案易于推导和实现。
4. Stripe Indexing (Single Shot)
条纹索引对于实现鲁棒的三维曲面重建是必要的,因为条纹的观察顺序不一定与条纹的投影顺序相同。这是由于基于三角测量的三维表面成像系统中存在的固有视差,以及由于物体三维表面特征的遮挡而导致获取的图像中缺少条纹的可能性。我们现在介绍一些有代表性的条纹索引技术。
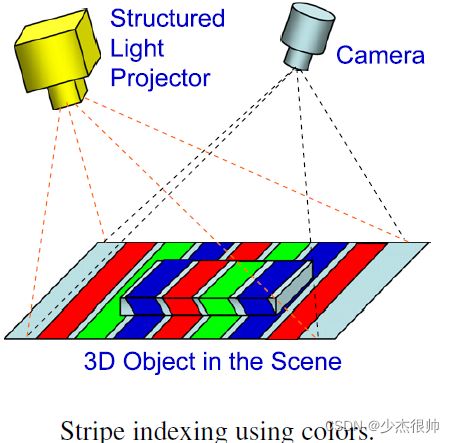
4.1. Stripe Indexing Using Colors
彩色图像传感器通常有三个独立的采集通道,每个通道对应一个光谱带。这些颜色分量的值的线性组合可以产生无限多的颜色。三个8位通道可以代表 2 24 2^{24} 224种不同的颜色。这种丰富的颜色信息可用于提高3D成像精度和缩短采集时间。例如,在投影图案(如下图)中使用颜色进行条纹索引有助于缓解使用单色图案的相移或多条纹技术所面临的模糊问题。这种类型的彩色编码系统可以实现实时三维表面成像能力。还可以将多个图案编码为单色投影图像,每个图案在颜色空间中具有唯一的颜色值。为了降低解码错误率,可以选择一种颜色集,其中每种颜色与该颜色集中的任何其他颜色都有最大距离。集合中的最大颜色数被限制为在获取的图像中产生最小串扰的颜色之间的距离。
4.2. Stripe Indexing Using Segment Pattern
为了区分一个条纹和其他条纹,可以向每条条纹添加一些独特的线段图案(如下图),以便在执行3D重建时,算法可以使用每条条纹的独特线段图案来区分它们。这种索引方法既有趣又聪明,但它仅适用于表面光滑且连续的3D对象,因为表面形状导致的图案变形并不严重。否则,由于图案的变形或物体表面的不连续性,可能很难恢复独特的分段图案。

4.3. Stripe Indexing Using Repeated Gray-Scale Pattern
如果使用了两个以上的强度级别,则可以排列条纹的强度级别,以使任何一组条纹(N个条纹的滑动窗口)在一段时间内具有唯一的强度模式。例如,如果使用三个灰度级(黑色、灰色和白色),则可以将图案设计为(如下图)。
B W G W B G W G B G W B G B W B G W BWGWBGWGBGWBGBWBGW BWGWBGWGBGWBGBWBGW

图案匹配过程从获取的图像强度与投影强度图案的相关性开始。一旦找到匹配项,将对亚灰度序列匹配项执行进一步搜索,例如三个字母序列WGB、GWB等。
4.4. Stripe Indexing Based on De Bruijn Sequence
大小为k的字母表上,n级的De Bruijn序是一个循环词(圆),其中每个长度为n的 k n k^n kn单词在圆中出现一次。下图显示了一个简单的De Bruijn圆示例,其中包含N=3和K=2(字母表为{0,1})。当我们绕着这个周期(顺时针或逆时针)运行时,我们会遇到 2 3 = 8 2^3=8 23=8个三位数模式000、001、010、011、100、101、110、111中的每一个,精确一次。序列中没有重复的三位数模式。换句话说,没有子序列与De Bruijn序列中的任何其他子序列相关。De Bruijn序列的这一独特特征可用于构建一个条纹图案序列,该序列具有独特的局部变异图案,不会重复自身。这种独特性使模式解码变得更容易。与De Bruijn序列相关联的图称为De Bruijn图。

现在我们展示一个使用RGB颜色二进制组合的例子,根据De Bruijn序列生成颜色索引条纹。三种颜色组合的最大数量为8( = 2 3 =2^3 =23)。因为我们不打算使用(0,0,0),所以我们只有七种可能的颜色。这个问题可以通过用k=7,n=3构造一个debruijn序列来解决。这就形成了一个343条条纹的序列。如果条纹的数量太多,可以通过设置K=5,N=3来使用De Bruijn序列的缩减集。在这种情况下,条纹的数量减少到125条。使用De Bruijn技术构造颜色索引条纹序列有一个重要的限制:所有相邻条纹必须具有不同的颜色。否则,会出现一些两倍或三倍宽度的条纹,混淆三维重建算法。通过使用XOR操作符,可以轻松应用此约束。下图显示了一组具有实际颜色索引条纹图案的结果。在这个条纹序列中,所有相邻的条纹都有不同的颜色。De Bruijn技术实现的各种变体可用于为3D表面成像应用生成独特的颜色索引、灰度索引或其他类型的投影图案。

5. Grid Indexing: 2D Spatial Grid Patterns
二维网格图案技术的基本概念是唯一地标记投影二维图案中的每个子窗口,以便任何子窗口中的图案都是唯一的,并且相对于其在图案中的二维位置完全可识别。
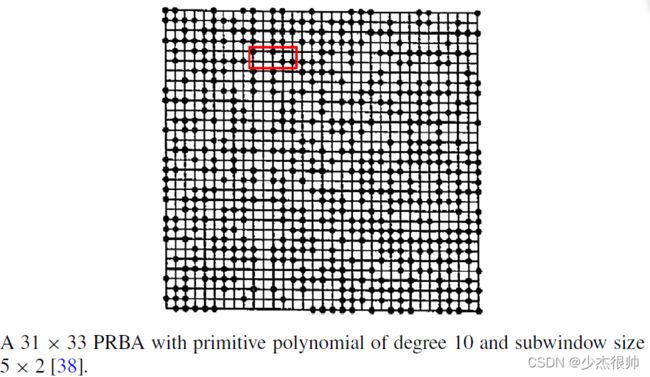
5.1. Pseudo-random Binary Array (PRBA)
一种网格索引策略是使用伪随机二进制数组(PRBA)生成可以用点或其他图案标记的网格位置,这样任何子窗口的编码图案都是唯一的。PRBA由使用伪随机序列编码的 n 1 × n 2 n_1×n_2 n1×n2数组定义,这样,使任何k1通过k2子窗口滑动整个阵列都是唯一的,并且完全定义了子窗口的绝对坐标(i,j)。二进制数组的编码图案基于伪随机二进制序列,使用原始多项式模 2 n 2^n 2n方法生成,其中 2 n − 1 = 2 k 1 k 2 − 1 , n 1 = 2 k 1 − 1 , n 2 = 2 n − 1 / n 1 2^n-1=2^{k_1k_2}-1,n_1=2^{k_1}-1,n_2=2^n-1/n_1 2n−1=2k1k2−1,n1=2k1−1,n2=2n−1/n1。下图显示了生成的PRBA示例,其中 k 1 = 5 , k 2 = 2 , n 1 = 31 , n 2 = 33 k_1=5,k_2=2,n_1=31,n_2=33 k1=5,k2=2,n1=31,n2=33。
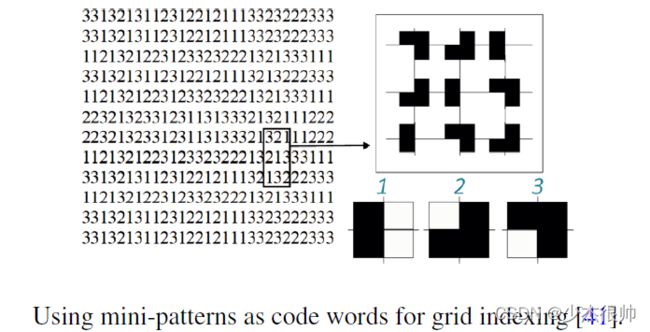
5.2. Mini-patterns Used as Code Words
可以使用多值伪随机数组,而不是使用伪随机二进制数组。可以用一个迷你图案作为特殊的码字来表示每个值,从而形成一个网格索引投影模式。下图显示了一个三值伪随机数组和一组迷你图案码字的示例(如图右下方所示)。使用特殊定义的码字,多值伪随机数组可以转换为具有唯一子窗口的投影模式。
5.3. Color-Coded Grids
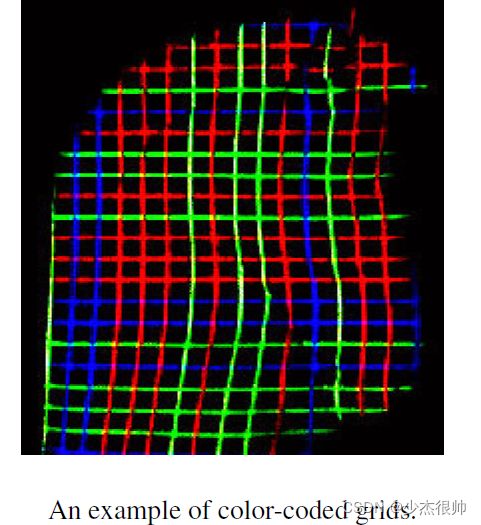
另一种网格索引策略是对垂直和水平条纹进行颜色编码,以便实现二维网格索引。垂直和水平条纹编码方案可以相同,也可以完全不同,这取决于应用(如下图)。无法保证子窗口的唯一性,但在大多数情况下,两个方向上的彩色条纹可以帮助解码建立对应关系。细网格线在图案提取中可能不如其他图案(点、正方形等)可靠。
5.4. 2D Array of Color-Coded Dots
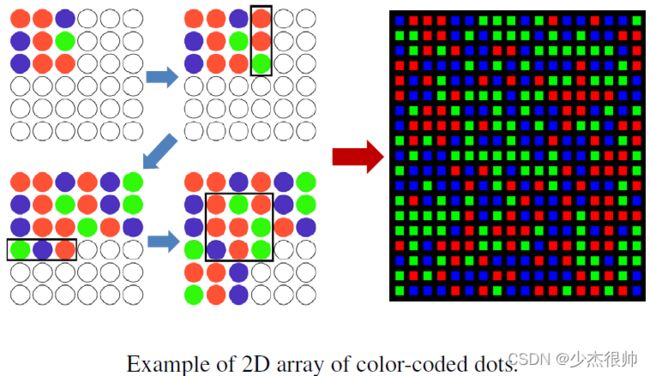
有其他生成伪随机数组的方法。如有一种蛮力算法来生成保留子窗口唯一性的数组,但它可能不会耗尽所有可能的子窗口图案。这种方法在计算机算法中实现起来比较直观。例如,如下图(左)显示了使用三个码字(R、G、B)的子窗口大小为3 × 3的6 ×6数组。计算过程如下:首先用随机选择的图案填充6 × 6数组的左上角。然后,在右边添加一个带有随机码字的三元素列。在添加这样的列之前,会验证子窗口的唯一性。继续添加列,直到所有列都填充了随机码字,并且验证了子窗口的唯一性。类似地,从初始子窗口位置向下添加随机行。然后,沿对角线方向添加新的随机码字。重复这些步骤,直到所有点都充满颜色。同样,这种计算过程可能无法保证为所有数组大小和码字生成伪随机数组,但在许多情况下都取得了良好的效果。下图(右)显示了一个20 ×18维伪随机数组的示例。
5.5. Hybrid Methods
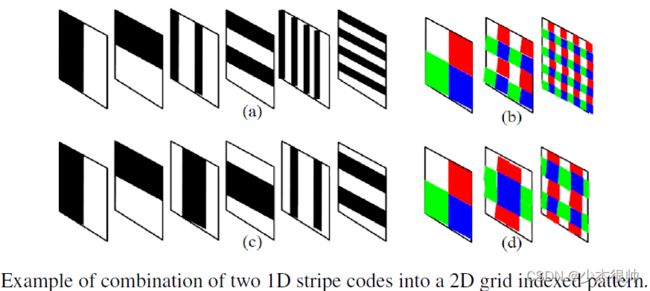
通过结合以上讨论的多种编码方案,有很多机会提高3D表面成像系统性能的特定方面。下图显示了一个示例
6. Performance Evaluation of 3D Surface Imaging Systems
三维表面成像系统的技术性能有很多因素。从应用角度来看,以下三个方面通常被用作评估3D成像系统的主要性能指标:
- 精度。精确测量表示3D表面成像系统获得的测量值与3D物体实际尺寸的最大偏差。通常,3D成像系统在不同的(x,y,z)方向下可能具有不同的精度,因为系统的固有设计特性。此外,不同的制造商可能会使用不同的方法来描述精度。例如,有些可能使用平均(平均)误差、不确定度、误差、均方根值或其他统计值。因此,在比较不同的系统时,必须理解任何性能声明的确切含义,并在同一框架内进行比较。
- 分辨率。在大多数光学文献中,光学分辨率被定义为光学系统区分图像中单个点或线的能力。类似地,3D图像分辨率表示3D成像系统可以分辨的物体表面的最小部分。然而,在3D成像领域,术语“图像分辨率”有时也表示系统在单帧中能够获得的最大测量点数量。例如,具有640 ×480像素的3D传感器可能能够为单次激发采集生成307200个测量点。给定视场、相隔距离和其他因素,这两种图像分辨率定义可以相互转换。
- 速度。采集速度对于成像移动对象(如人体)非常重要。对于单镜头3D成像系统,帧速率表示其在短时间间隔内重复全帧采集的能力。对于顺序3D成像系统(例如,激光扫描系统),除了帧速率之外,还需要考虑另一个问题:在执行顺序采集时,对象正在移动;因此,获得的全帧3D图像可能不代表3D对象在单个位置的快照。相反,它变成了在不同时间点上获取的测量点的集成;因此,3D形状可能会从3D对象的原始形状变形。在采集速度和计算速度之间还有另一个区别。例如,一些系统能够以30帧/秒的速度获取3D图像,但这些获取的图像需要以较慢的帧速率进行后处理以生成3D数据。
上述三个关键性能指标可用于比较3D成像系统。下图显示了一个主要的性能空间,其中每个3D成像方法可能占据一个点,然后可以直观地比较多个3D成像系统。当然,在评估3D表面成像系统的实际安装时,系统的性价比和可靠性也是重要的考虑因素。

除了主要的性能指标外,几乎有无限数量的性能指标可用于描述3D成像系统的各个特定方面。例如,3D成像系统的景深是指能够获得精确3D测量的距离范围。最终,这些类型的系统特性将反映在主要性能指标上(例如,测量精度、分辨率和速度)。
视野、基线和相隔距离也可用于描述3D成像系统的行为。由于光投射的能量有限,结构光3D成像系统通常具有有限的相隔距离,而依赖单个激光扫描的飞行时间传感器可以达到英里的距离。
每种类型的3D成像技术都有其优缺点,我们应该根据预期应用的总体性能来判断系统。
7. Camera and Projector Calibration Techniques
三维成像技术的一个重要组成部分是摄像机和投影仪的标定技术,它们在确定三维成像系统的测量精度方面起着关键作用。摄像机标定是计算机视觉中一个众所周知的问题。然而,令人惊讶的是,3D成像技术的这一关键方面在许多3D成像技术评论、研究和应用文章中没有得到足够的重视。由于大多数3D成像系统使用2D光学传感器,摄像机标定程序在考虑镜头畸变的情况下,建立2D图像上的像素(在摄像机坐标中)与物体点所在的3D空间(世界坐标)中的直线之间的关系。通常,使用一个简化的摄像机模型和一组内在参数来描述这些关系。有几种方法和附带的工具箱。这些程序通常需要已知校准对象的多个角度和距离的图像。平面棋盘格图案是一种常用的校准对象,因为其制作非常简单,可以用标准打印机打印,并且具有易于检测的独特角点。下图中示出了涉及这种图案的示例图像。从校准模式的图像构建二维到三维的对应关系。

7.1. Camera Calibration Algorithms
假设平面标定板在世界坐标系中的平面为Z =0;然后,标定板上的每个点都变成 M = [ X , Y , 0 , 1 ] T M=[X,Y,0,1]^T M=[X,Y,0,1]T 。因此,对象点M及其像点m由单应矩阵H关联:
m ~ K [ r 1 , r 2 , r 3 , − R t ] [ X , Y , 0 , 1 ] T {m~K[r_1,r_2,r_3,-Rt][X,Y,0,1]^T} m~K[r1,r2,r3,−Rt][X,Y,0,1]T
m ~ H [ X , Y , 1 ] T {m~H[X,Y,1]^T} m~H[X,Y,1]T
其中 H = [ h 1 , h 2 , h 3 ] = K [ r 1 , r 2 , − R t ] H=[h_1,h_2,h_3]=K[r_1,r_2,-Rt] H=[h1,h2,h3]=K[r1,r2,−Rt]是按比例定义的3 × 3矩阵, r 1 r_1 r1, r 2 r_2 r2, r 3 r_3 r3是旋转矩阵的3 ×1列向量。注意,对于旋转矩阵R,列向量 r 1 r_1 r1, r 2 r_2 r2, r 3 r_3 r3是正交的,因此我们有:
h 1 T ( K K T ) − 1 h 2 T = 0 h^T_1(KK^T)^{-1}h_2^T=0 h1T(KKT)−1h2T=0
h 1 T ( K K T ) − 1 h 1 T = h 2 T ( K K T ) − 1 h 2 T h^T_1(KK^T)^{-1}h_1^T=h^T_2(KK^T)^{-1}h_2^T h1T(KKT)−1h1T=h2T(KKT)−1h2T
每个单应性可以提供两个内参约束。 K − T K − 1 K^{-T}K^{-1} K−TK−1在上面的等式中是一个对称矩阵,它可以用6D向量定义:
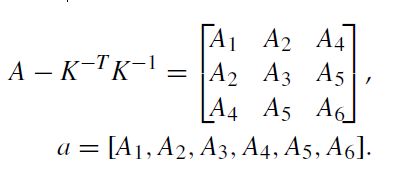
(注:这里的 A − K − T K − 1 A-K^{-T}K^{-1} A−K−TK−1应该为 A = K − T K − 1 A=K^{-T}K^{-1} A=K−TK−1)
设H的第i列向量为 h i = [ h i 1 , h i 2 , h i 3 ] h_i=[h_{i1},h_{i2},h_{i3}] hi=[hi1,hi2,hi3]。那么,我们有
h i T A h j = v i j a h^T_iAh_j=v_{ij}a hiTAhj=vija
其中 v i j = [ h i 1 h j 1 , h i 1 h j 2 + h i 2 h j 1 , h i 2 h j 2 , h i 3 h j 1 + h i 1 h j 3 , h i 3 h j 2 + h i 2 h j 3 , h i 3 h j 3 ] T v_{ij}=[h_{i1}h_{j1},h_{i1}h_{j2}+h_{i2}h_{j1},h_{i2}h_{j2},h_{i3}h_{j1}+h_{i1}h_{j3},h_{i3}h_{j2}+h_{i2}h_{j3},h_{i3}h_{j3}]^T vij=[hi1hj1,hi1hj2+hi2hj1,hi2hj2,hi3hj1+hi1hj3,hi3hj2+hi2hj3,hi3hj3]T。然后,这两个约束可以重写为齐次方程。为了解出a,至少需要三张来自不同视点的图像。在实际应用中,使用更多的图像来减少噪声的影响,并通过奇异值分解得到最小二乘误差解。最后,可以通过最小化以下函数来优化结果,以最小化重投影误差:
∑ i = 1 n ∑ j = 1 m ∣ ∣ m i j − m ^ ( K , R , t , M j ) ∣ ∣ 2 \sum_{i=1}^{n}\sum^{m}_{j=1}{||m_{ij}-\hat{m}(K,R,t,M_j)||^2} i=1∑nj=1∑m∣∣mij−m^(K,R,t,Mj)∣∣2
7.2. Projector Calibration
投影仪的校准有两个方面:作为主动光源,需要校准投影仪的强度,以恢复其照明强度的线性;作为逆相机,需要像普通相机一样进行几何校准。
7.2a. Intensity Calibration of Projector
为了增强对比度,投影仪供应商经常通过伽马变换改变投影仪的强度曲线。在3D成像系统中用作主动光源时,需要进行校准以恢复照明强度的线性。为此,投影多个测试图案,并由成像传感器捕捉投影图案。可以建立投影图案的实际强度与图像像素值之间的关系,然后用高阶多项式函数拟合。然后,计算逆函数,并将其用于校正3D成像过程中要投影的图案(如下图)
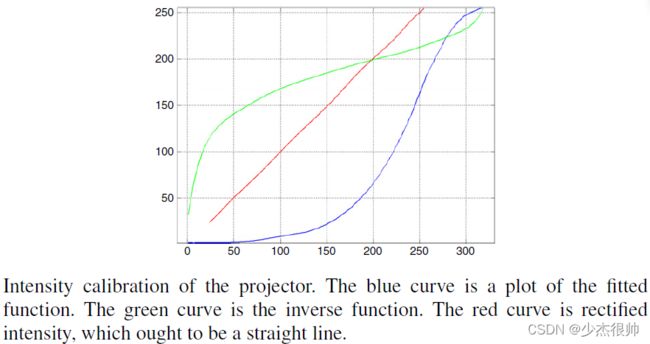
7.2b. Geometric Calibration of Projector
将投影仪视为逆相机;投影仪的光学模型与相机相同,唯一的区别是投影方向。逆模型使得将2D图像(在相机坐标中)上的像素与3D空间(世界坐标)中的直线相关联的问题变得困难,因为我们无法判断3D空间中的给定点在逆相机坐标中的投影位置。投影仪校准的关键问题是如何建立对应关系。一旦建立了对应关系,就可以使用摄像机校准算法对投影仪进行校准。
投影仪校准是使用预先校准的摄像机和校准平面进行的。首先,在摄像机坐标系中恢复校准平面。然后,校准图案(如下图)被投影并被相机捕捉。在校准平面上形成的棋盘图案的角点的三维坐标可以通过将捕获图像上的角点重新投影到标定板上来确定,因为相机和标定板之间的空间关系已经恢复。最后,利用获取的点对应关系对投影仪进行标定。这种方法在理论上简单易行。然而,这些方法的校准精度在很大程度上取决于相机预校准的精度。

8. Application Examples of 3D Surface Imaging Technologies
我们提供了几个3D成像技术有趣应用的示例。这些例子并非详尽无遗,由于篇幅有限,我们无法在这里介绍许多应用程序。
8.1. 3D Facial Imaging
人体部位是3D成像的理想对象。每个人的身体部位都不一样。没有人体的数字CAD模型;因此,每个身体部位都需要通过3D成像技术进行建模。下图显示了作者开发的3D相机拍摄的3D面部图像示例。显示了三维曲面数据的着色模型和线框模型。3D人脸图像有很多应用,从3D人脸识别和整形手术到由主人的3D人脸制作的个性化礼物。

8.2. 3D Dental Imaging
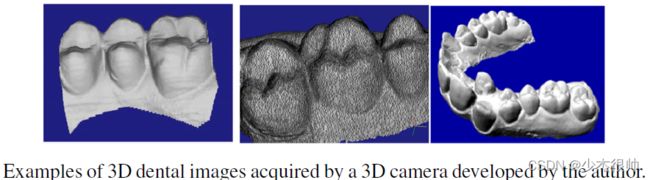
下图显示了一些由作者开发的3D相机拍摄的3D牙齿图像示例。通常,单个3D图像(左)覆盖牙弓结构的一小部分。拍摄多张3D图像以覆盖整个牙弓表面,3D图像拼接软件将这些多张3D图像无缝拼接在一起,形成整个牙弓的3D模型(右图)。
8.3. 3D Imaging Techniques for Plastic Surgery
3D成像系统使整形外科医生能够捕捉并显示患者乳房的3D表面轮廓,用于评估、术前治疗计划、治疗后验证、患者沟通和记录。3D相机能够捕捉所有3D表面数据(x,y,z)坐标和关联的2D图像纹理数据(颜色叠加)。下图显示了使用3D成像技术进行3D手术规划的示例。医生和患者可以使用3D摄像机获取的患者特定的乳房3D轮廓,根据植入物的选择检查模拟结果,根据体积测量和可能的不对称性,帮助确定合适的植入物。

8.4. 3D Model of Ear Impression for a Custom-Fit Hearing Aid
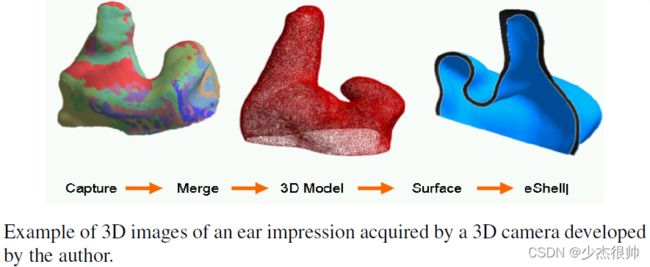
根据国家耳聋与沟通障碍研究所(NIDCD)的统计数据,超过2800万美国人患有不同程度的听力障碍。目前定制助听器的生产过程是劳动密集型的,返修率约为翻拍率的三分之一。3D成像技术可以取代传统的物理印象,从而消除与这种容易出错且不舒服的过程相关的成本和时间。数字成像使助听器制造商能够利用计算机辅助设计(CAD)和制造(CAM)技术的最新突破,在一天的时间内生产定制的助听器设备(如下图)。
8.5. 3D Imaging for Reverse Engineering
许多符合人体工程学的产品都是通过手工制作的原型,因此设计师可以获得外形轮廓的触感和感觉,并对其进行优化,直到“感觉良好”这种手工制作的原型可以通过使用3D摄像系统转换为3D CAD文件。下图显示了一个鼠标设计的3D CAD文件示例,该文件是使用作者制作的3D相机数字化的。

8.6. 3D Imaging System for Airbag Analysis
为了优化安全气囊的设计,确保驾驶员和乘客的安全,高速三维表面和体积测量以及跟踪能力对于表征安全气囊的动态行为非常重要。传统上,获取气囊爆炸过程中的三维表面和体积测量非常困难。由于3D成像技术的进步,现在可以获取气囊的精确连续3D表面和体积数据。下图显示了在测试安全气囊爆炸期间获得的动态3D数据序列的示例。这些类型的3D数据有助于对安全气囊的行为进行定量分析,并为优化安全气囊设计提供关键手段。

8.7. High-Speed 3D Imaging System for Vehicle Crash Tests
偏置碰撞最有害的方面是车厢侵入和侵犯乘员的生存空间,其中只有车辆前部结构的一部分被加载。与碰撞完成后测量的最终侵入程度相比,偏置碰撞的伤害后果与相对于受影响身体部位的侵入时间、位置和速度的关系更为密切。在侧面碰撞、侧翻和其他碰撞模式中,侵入也是一个有害因素。美国国家公路交通安全管理局(NHTSA)正在评估偏置碰撞试验,作为未来可能的正面保护要求。为了有效和定量地评估此类影响,需要一个动态入侵传感系统,该系统可以在分阶段碰撞试验期间对车厢入侵进行动态测量。高速3D成像技术能够在碰撞试验中提供车辆各部分结构变形的精确定量测量数据。下图显示了使用各种3D数据可视化模式进行测试的门板的全帧3D图像示例。

8.8. 3D Imaging Technology for Accident Scene Investigation
交通事故现场可能非常复杂,有争议的解释,法律代表很难准确沟通。争议可能会产生,通常会导致昂贵且耗时的法律程序。3D成像技术可以帮助准确记录事故现场,从而为法律和保险案件提供有效工具。三维事故现场重建能够清晰有效地描述事故事实。事故现场可以从几乎无限多个可能的有利位置从任何摄像机角度重新拍摄(如下图)。

9. Conclusions
本教程全面回顾了结构光三维表面成像技术的最新进展,并举例说明了其在各个领域的应用。我们建立了一个分类框架,以适应各种各样的3D成像技术,并以系统的方式组织和呈现。本文简要介绍了代表性的技术,并提供了插图,以帮助读者掌握其基本概念。综述了三维成像系统的性能指标,介绍了摄像机和投影仪的标定技术。介绍了3D成像技术应用的一些示例。
到目前为止,有这么多3D成像技术被开发出来,这是有原因的。没有一种技术可以应用于每个应用场景。每种3D成像技术都有自己的优缺点。当选择用于特定应用的3D成像技术时,鼓励读者在它们的特定应用要求之间进行仔细权衡,并考虑诸如精度、分辨率、速度、成本和可靠性等关键性能指标。有时,需要多模态传感器系统来满足单一模态无法满足的需求。
3D成像是一项跨学科技术,它的贡献来自光学设计、结构设计、传感器技术、电子、封装以及硬件和软件。传统上,这些学科的三维成像研究活动或多或少是独立进行的,侧重点不同。三维成像研究的最新趋势要求采用一种综合方法,有时称为“计算成像”方法,其中光学设计、传感器特性和软件处理能力同时考虑。这一新方法有望显著提高未来三维成像系统的性能和性价比,是未来三维成像技术发展的一个有价值的方向。
非常棒非常详细的一篇综述文章,大家看完点点赞呀。(文献引用在段首,大家感兴趣的话可以去看原文献)