SS【1】：转置卷积与膨胀卷积

---

前言

本文首先回顾了普通的直接卷积操作，然后讲解了在语义分割中十分常见的两种卷积操作：转置卷积（Transposed Convolution）与膨胀卷积（Dilated Convolution）

同时，还给出了相关实例，方便读者理解。具体的语义分割模型的网络结构讲解，可以参考博主主页中的其他blog

---

1. Convolution

1.1. Introduction

• padding = 0
• strides = 1
• kernal_size = 3

假设输入特征图大小是 4x4 的（假设输入输出都是单通道），通过卷积后得到的特征图大小为 2x2。一般使用卷积的情况中，要么特征图变小（stride > 1），要么保持不变（stride = 1），当然也可以通过四周 padding 让特征图变大但没有意义。关于卷积的详细介绍以及如何使用 Pytorch 实现卷积操作，可以看我的另一篇 blog：CV学习笔记【2】：卷积与Conv2d

1.2. Procedure

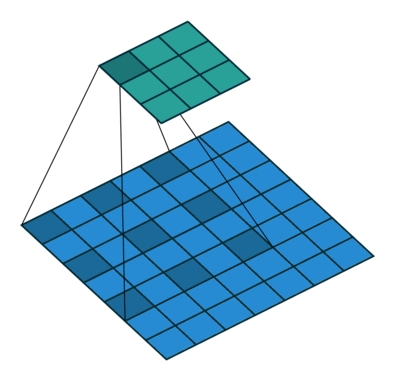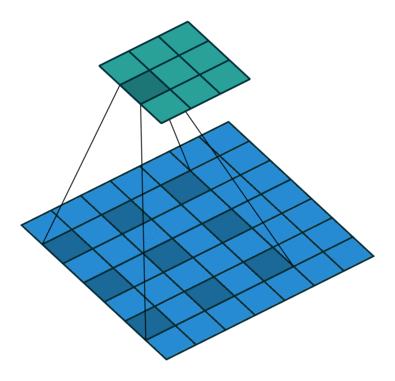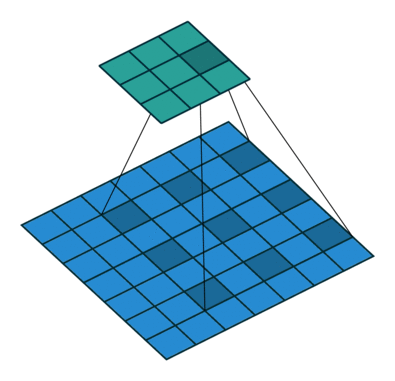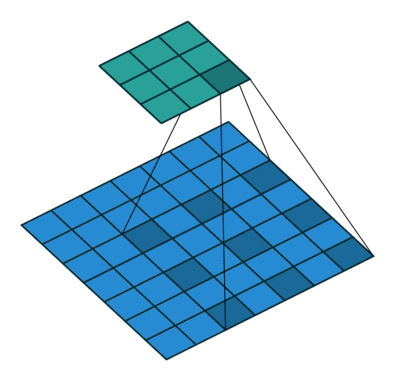
普通的卷积过程可以直观的理解为一个带颜色小窗户（卷积核）在原始的输入图像一步一步的挪动，来通过加权计算得到输出特征：

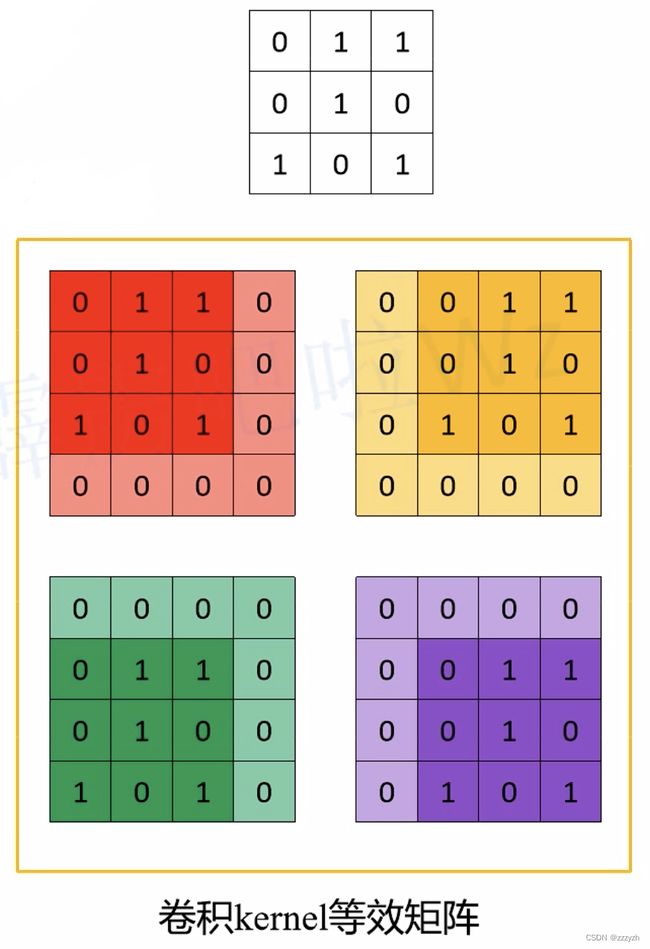
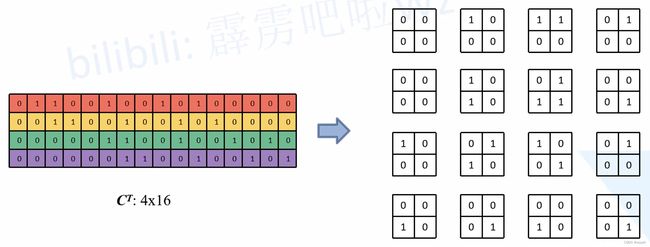
但是实际在计算机中计算的时候，并不是像这样一个位置一个位置的进行滑动计算，因为这样的效率太低了。计算机会将卷积核转换成等效的矩阵，将输入转换为向量。通过输入向量和卷积核矩阵的相乘获得输出向量。输出的向量经过整形便可得到我们的二维输出特征。具体的操作如下图所示。由于我们的 3x3 卷积核要在输入上不同的位置卷积 4 次，所以通过补零的方法将卷积核分别置于一个 4x4 矩阵的四个角落。这样我们的输入可以直接和这四个 4x4 的矩阵进行卷积，而舍去了滑动这一操作步骤：

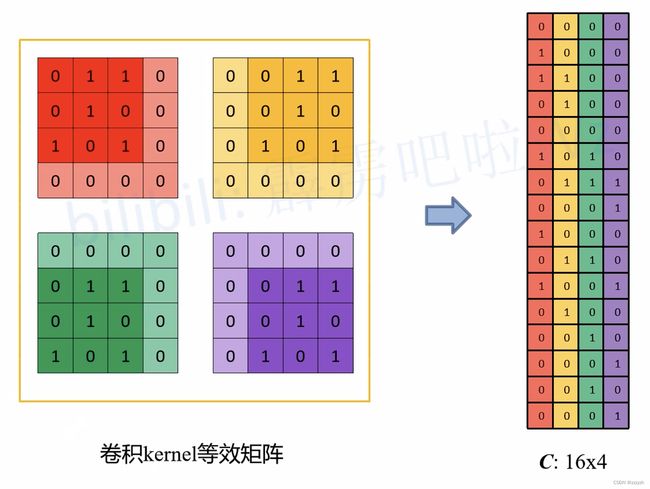
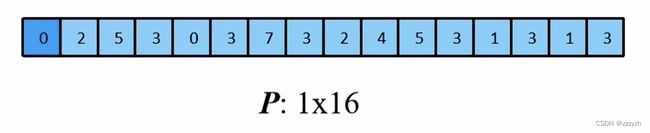
进一步的，我们将输入拉成长向量，四个 4x4 卷积核也拉成长向量并进行拼接：

• 输入
  
• 卷积核
  

我们记向量化的图像为 $I$，向量化的卷积矩阵为 $C$，输出特征向量为 $O$，则有：

$$I^T\ast C=O^T$$

最终计算过程如下图所示:

$$I^{1\times 16}{C}^{16\times 4}=O^{1\times 4}$$

---

2. Transposed Convolution

2.1. Introduction

转置卷积（Transposed Convolution） 在语义分割或者对抗神经网络（GAN）中比较常见，其主要作用就是做上采样（UpSampling）。在有些地方转置卷积又被称作 fractionally-strided convolution 或者 deconvolution，但 deconvolution 具有误导性，不建议使用。对于转置卷积需要注意的是：

• 转置卷积不是卷积的逆运算
  • 转置卷积只是将特征层的大小还原回卷积之前的大小，但是还原后的特征层中的数值与原本的数值并不相同，所以不能认为是“逆运算”
• 转置卷积也是卷积

2.2. Procedure

转置卷积的运算步骤可以归为以下几步：

• 在输入特征图元素间填充 s-1 行、列 0（其中 s 表示转置卷积的步距）
  
  • s = 1、s - 1 = 0，即不需要在元素间填充行和列
    
  • s = 2、s - 1 = 1，即需要在元素间填充 1 行和 1 列 0
• 在输入特征图四周填充 k-p-1 行、列 0（其中 k 表示转置卷积的 kernel_size 大小，p 为转置卷积的 padding，注意这里的 padding 和卷积操作中有些不同）
  
  • k = 3、p = 0、k - p - 1 = 2，即需要在特征图四周填充 2 行和 2 列 0
    
  • k = 3、p = 1、k - p - 1 = 1，即需要在特征图四周填充 1 行和 1 列 0（在第一步的基础上）
• 将卷积核参数上下、左右翻转
• 做正常卷积运算（填充 0，步距 1）

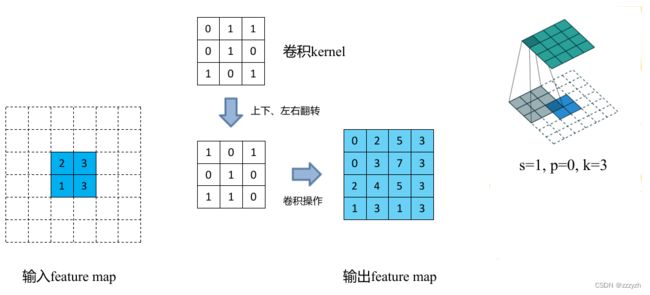
假设输入的特征图大小为 2x2（假设输入输出都为单通道），通过转置卷积后得到 4x4 大小的特征图。这里使用的转置卷积核大小为 k = 3，stride = 1，padding = 0 的情况（忽略偏执bias）：

• 首先在元素间填充 s-1 = 0 行、列 0（等于 0 不用填充）
• 然后在特征图四周填充 k-p-1 = 2 行、列 0
• 接着对卷积核参数进行上下、左右翻转
• 最后做正常卷积（填充 0，步距 1）

转置卷积操作后特征图的大小可以通过如下公式计算：

$$\begin{gathered} H_{out}=(H_{in}-1)\times stride[0]-2\times padding[0]+kerne{l}_{s}ize[0] \\ {W}_{out}=(W_{in}-1)\times stride[1]-2\times padding[1]+kerne{l}_{s}ize[1] \end{gathered}$$

• stride[0] 表示高度方向的 stride，padding[0] 表示高度方向的 padding，kernel_size[0] 表示高度方向的 kernel_size
• stride[1] 表示高度方向的 stride，padding[1] 表示高度方向的 padding，kernel_size[1] 表示高度方向的 kernel_size

通过上面公式可以看出 padding 越大，输出的特征矩阵高、宽越小，你可以理解为正向卷积过程中进行了 padding 然后得到了特征图，现在使用转置卷积还原到原来高、宽后要把之前的 padding 减掉

2.3. torch.nn.ConvTranspose2d

torch.nn.ConvTranspose2d 参数如下：

• in_channels：输入图片的通道数
• out_channels：输出图片的通道数
• kernel_size：卷积核的大小
• stride：步长
• padding：填充
• output_padding：在计算得到的输出特征图的高、宽方向各填充几行或列 0（注意，这里只是在上下以及左右的一侧 one side 填充，并不是两侧都填充），默认为 0 不使用
• groups：当使用到组卷积时才会用到的参数，默认为 1 即普通卷积
• bias：是否使用偏执 bias，默认为 True 使用。
• dilation：当使用到空洞卷积（膨胀卷积）时才会使用到的参数，默认为 1 即普通卷积

输出特征图宽、高计算：

$$\begin{gathered} H_{out}=(H_{in}-1)\times stride[0]-2\times padding[0]+dilation[0]\times (kerne{l}_{size}[0]-1)+outpu{t}_{p}adding[0]+1 \\ {W}_{out}=(W_{in}-1)\times stride[1]-2\times padding[1]+dilation[1]\times (kerne{l}_{size}[1]-1)+outpu{t}_{p}adding[1]+1 \end{gathered}$$

2.4. Visualization

一般的卷积操作（我们这里只考虑最简单的无 padding，stride = 1 的情况），都将输入的数据越卷越小。根据卷积核大小的不同，和步长的不同，输出的尺寸变化也很大。

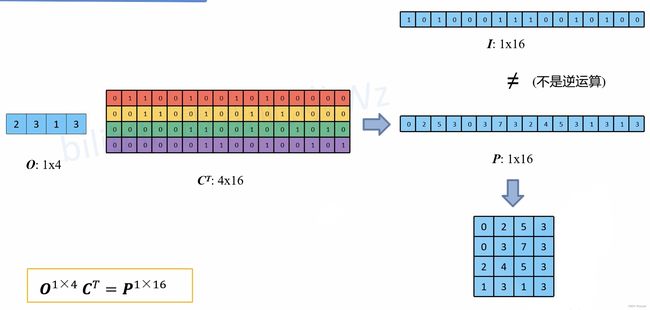
在数学上，转置卷积的操作非常简单，把正常卷积的操作反过来即可：

$$O^T\ast C^T=I^T$$

这里需要注意的是这两个操作并不是可逆的，对于同一个卷积核，经过转置卷积操作之后并不能恢复到原始的数值，保留的只有原始的形状

结果张量：

将输入还原为一个 2x2 的张量：

在正常卷积的操作过程中，直接卷积向量化的时候是将卷积核补零然后拉成列向量，得到了一个新的转置卷积矩阵，现在将这个过程反过来，把 16 个列向量再转换成卷积核：

推理过程如下：

• 以第一个等效矩阵为例：
  
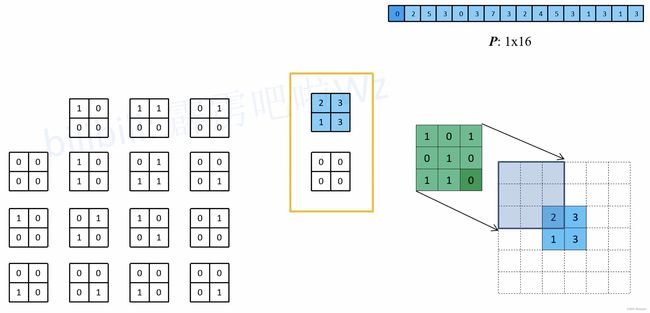
• 以第二个等效矩阵为例：
  
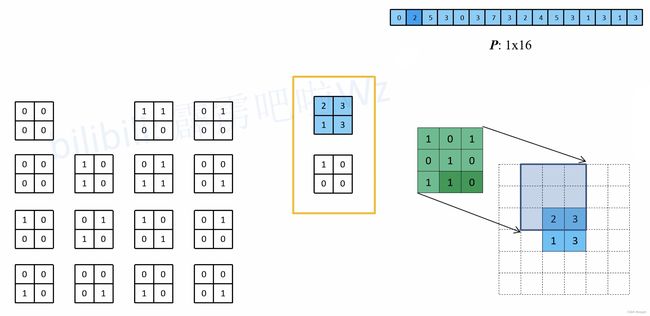
• 以第三个等效矩阵为例：
  
• 以第四个等效矩阵为例：
  
• 同理可以知道剩下的等效矩阵与卷积核卷积的结果
• 通过比较可以发现，使用的绿色卷积核，与一开始直接卷积的卷积核的关系为：原直接卷积卷积核上下、左右翻转后得到新卷积核
  

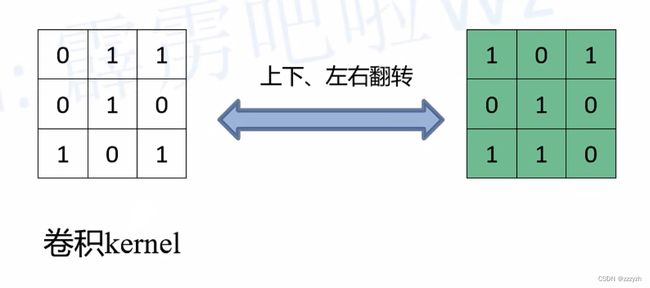
2.5. Experiment

下面使用 Pytorch 框架来模拟 s = 1，p = 0，k = 3 的转置卷积操作

在代码中 transposed_conv_official 函数是使用官方的转置卷积进行计算，transposed_conv_self 函数是按照上面讲的步骤自己对输入特征图进行填充并通过卷积得到的结果

import torch
import torch.nn as nn


def transposed_conv_official():
    feature_map = torch.as_tensor([[1, 0],
                                   [2, 1]], dtype=torch.float32).reshape([1, 1, 2, 2])
    print(feature_map)
    trans_conv = nn.ConvTranspose2d(in_channels=1, out_channels=1,
                                    kernel_size=3, stride=1, bias=False)
    trans_conv.load_state_dict({"weight": torch.as_tensor([[1, 0, 1],
                                                           [0, 1, 1],
                                                           [1, 0, 0]], dtype=torch.float32).reshape([1, 1, 3, 3])})
    print(trans_conv.weight)
    output = trans_conv(feature_map)
    print(output)


def transposed_conv_self():
    feature_map = torch.as_tensor([[0, 0, 0, 0, 0, 0],
                                   [0, 0, 0, 0, 0, 0],
                                   [0, 0, 1, 0, 0, 0],
                                   [0, 0, 2, 1, 0, 0],
                                   [0, 0, 0, 0, 0, 0],
                                   [0, 0, 0, 0, 0, 0]], dtype=torch.float32).reshape([1, 1, 6, 6])
    print(feature_map)
    conv = nn.Conv2d(in_channels=1, out_channels=1,
                     kernel_size=3, stride=1, bias=False)
    conv.load_state_dict({"weight": torch.as_tensor([[0, 0, 1],
                                                     [1, 1, 0],
                                                     [1, 0, 1]], dtype=torch.float32).reshape([1, 1, 3, 3])})
    print(conv.weight)
    output = conv(feature_map)
    print(output)


def main():
    transposed_conv_official()
    print("---------------")
    transposed_conv_self()


if __name__ == '__main__':
    main()

---

3. Dilated Convolution

3.1. Introduction

• kernel_size = 3
• padding = 0
• strides = 1
• r（膨胀因子）= 2
  • r = 1 即普通卷积

空洞卷积也叫扩张卷积或者膨胀卷积，简单来说就是在卷积核元素之间加入一些空格（0）来扩大卷积核的过程

3.2. Effects

Deep CNN存在一些主要的问题：

• 上采样和池化层存在一些知名的问题
• 内部数据结构丢失，空间层级化信息丢失
• 小物体无法重建

膨胀卷积的作用：

• 增大感受野
• 保持原输入特征图的 W、H

膨胀卷积的优点：

• 内部数据结构的保留
• 避免使用 down-sampling 这样的特性

3.3. Potential Problems

3.3.1. Gridding Effect

3.3.1.1. Problems

假设此时我们连续使用 3 个膨胀卷积层，每个膨胀卷积层的卷积核大小为 3，且膨胀系数为2：

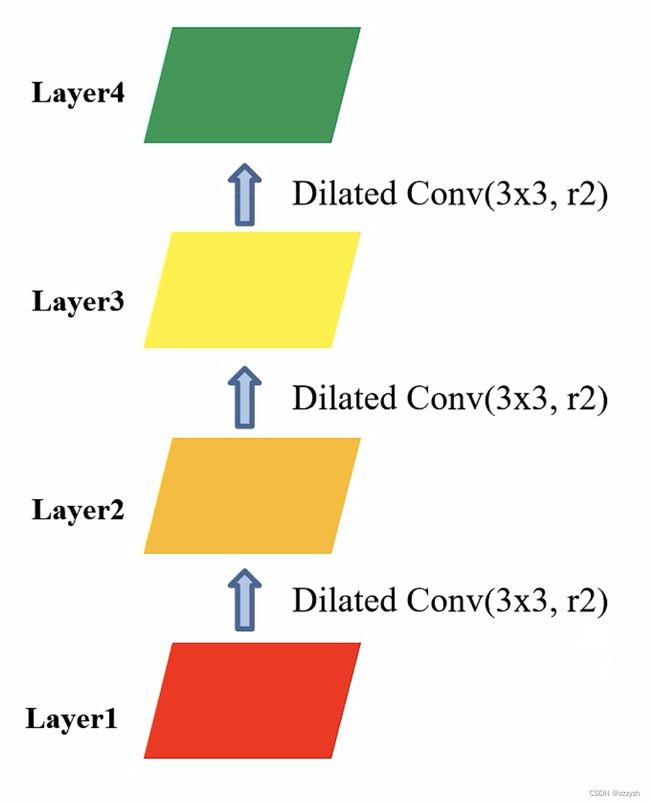
• 当我们连续使用 1 个膨胀系数为 2 的膨胀卷积层：Layer 2，Layer 2 上的 1 个 pixel 会使用 Layer 1 上的 9 个 pixel 位置上的参数
  
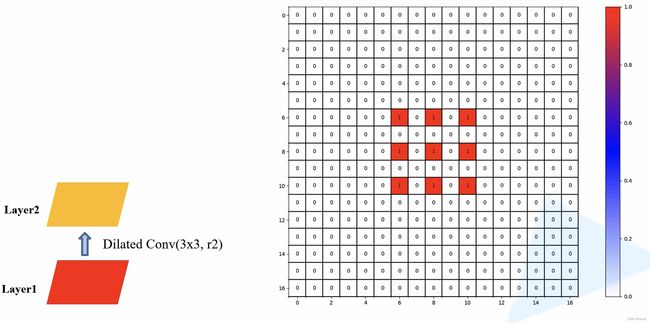
• 当我们连续使用 2 个膨胀系数为 2 的膨胀卷积层：Layer 2 和 Layer 3，Layer 3 上的 1 个 pixel 会使用 Layer 1 上的 25 个 pixel 位置上的参数，右侧图上 pixel 的数字表示Layer 3 上的 1 个 pixel 利用 Layer 1 上 的 pixel 的次数
  
• 当我们连续使用 3 个膨胀系数为 2 的膨胀卷积层：Layer 2、Layer 3 和 Layer 4，Layer 4 上的 1 个 pixel 会使用 Layer 1 上的 49 个 pixel 位置上的参数，右侧图上 pixel 的数字表示Layer 4 上的 1 个 pixel 利用 Layer 1 上 的 pixel 的次数
  
• 这个时候我们会发现，Layer 4 的 1 个 pixel 上使用到的 Layer 1 上的数据，并不是连续的，在每个非 0 元素之间存在一定间隔，即Gridding Effect，即 Layer 4 上的 1 个像素并没有利用到对应范围内的所有像素，所以会导致丢失一些细节信息

3.3.1.2. Solution

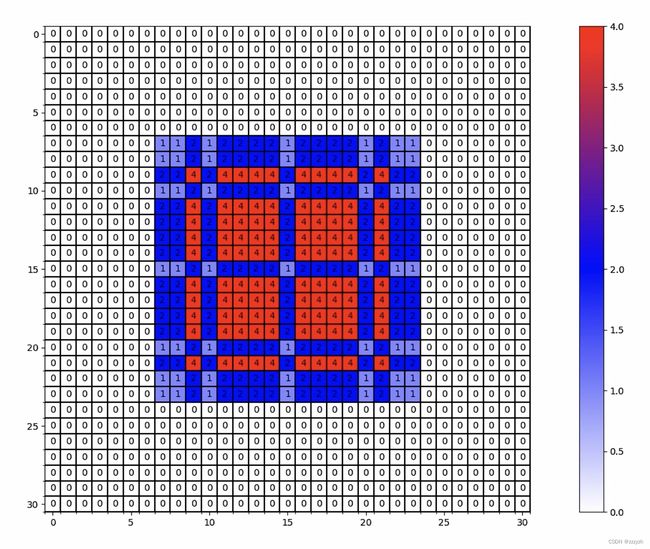
假设此时我们连续使用 3 个膨胀卷积层，每个膨胀卷积层的卷积核大小为 3，且膨胀系数依次为 1、2、3：

• 当我们使用 1 个膨胀系数为 1 的膨胀卷积层（即普通卷积）：Layer 2，Layer 2 上的 1 个 pixel 会使用 Layer 1 上的 9 个 pixel 位置上的参数
  
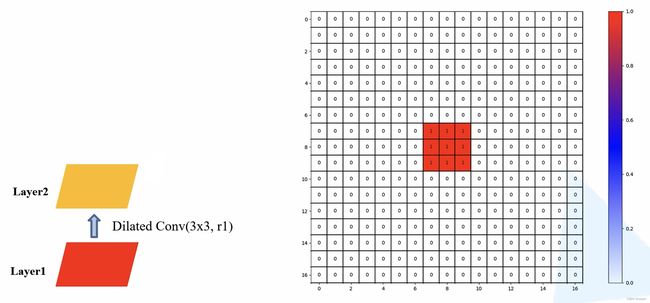
• 当我们连续使用 1 个膨胀系数为 1 的膨胀卷积层（即普通卷积）和 1 个膨胀系数为 2 的膨胀卷积层：Layer 2 和 Layer 3，Layer 3 上的 1 个 pixel 会使用 Layer 1 上的 7 个 pixel 位置上的参数，且这个 7x7 的区域内的每个 pixel 都有被利用到
  
• 当我们连续使用 1 个膨胀系数为 1 的膨胀卷积层（即普通卷积）、 1 个膨胀系数为 2 的膨胀卷积层和 1 个膨胀系数为 3 的膨胀卷积层：Layer 2、Layer 3 和 Layer 4，Layer 4 上的 1 个 pixel 会使用 Layer 1 上的 13 个 pixel 位置上的参数，且这个 13x13 的区域内的每个 pixel 都有被利用到，右侧图上 pixel 的数字表示Layer 3 上的 1 个 pixel 利用 Layer 1 上 的 pixel 的次数
  

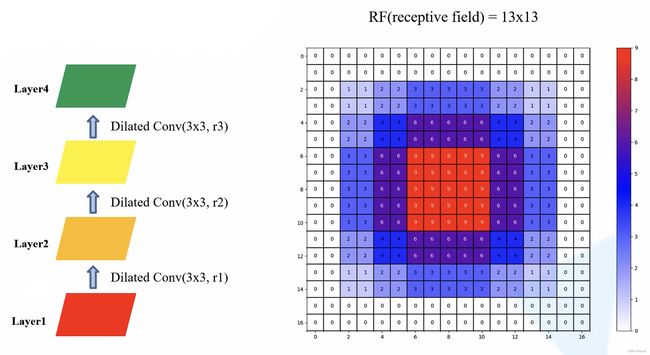
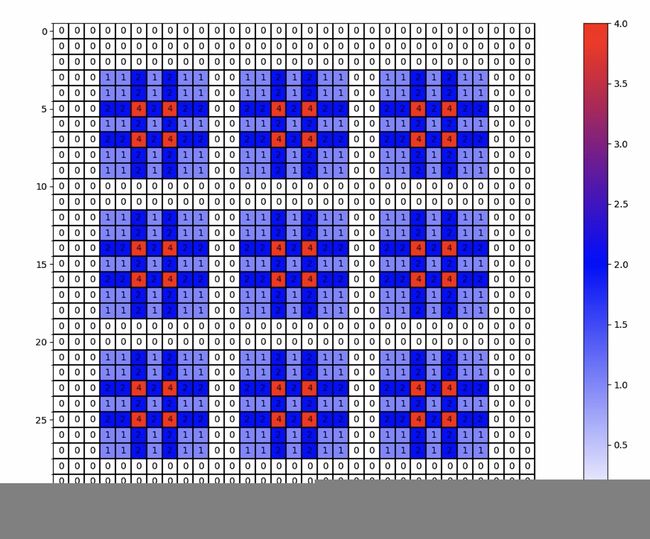
作为对比实验，假设连续使用 3 个普通卷积层，得到的结果如下所示：

• 在参数相同的情况下，使用膨胀卷积可以有效的增加感受野

3.3.2. Long-ranged information might be not relevant

从 dilated convolution 的设计背景来看就能推测出这样的设计是用来获取 long-ranged information。然而光采用大 dilation rate 的信息或许只对一些大物体分割有效果，而对小物体来说可能则有弊无利了。 如何同时处理不同大小的物体的关系，则是设计好 dilated convolution 网络的关键。

简单来说，就是空洞卷积虽然在参数不变的情况下保证了更大的感受野，但是对于一些很小的物体，本身就不要那么大的感受野来说，这是极度不友好的。

3.4. Hybrid Dilated Convolution

HDC 原则：

当使用到多个膨胀卷积时，需要设计各卷积核的膨胀系数（$[r_1,r_2,...,r_n]$）使其刚好能覆盖底层特征层

三个指标：

• 叠加卷积的 dilation rate 不能有大于1的公约数
• 将 dilation rate 设计成锯齿状结构
  
  • $r=[1,2,3,1,2,3]$
• 定义 maximum distance between two nonzero values，来限制膨胀系数的大小
  $$M_i=max[M_{i+1}-2r_i,M_{i+1}-2(M_{i+1}-r_i),r_i]$$
  • $M_i$：第 i 层两个非 0 元素的最大距离
  • $r_i$：第 i 层的膨胀系数
  • 设计目标是：$M_2\le K$，K 即 kernel_size
    • 例子：$K=3,r=[1,2,5]$
      • $M_2=2<K$
        • $M_3-2r_2=1,M_3-2(M_3-r_i)=-1,r_2=2$
      • 合理
    • 例子：$K=3,r=[1,2,9]$
      • $M_2=5>K$
      • 不合理

3.5. Experiment

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap


def dilated_conv_one_pixel(center: (int, int),
                           feature_map: np.ndarray,
                           k: int = 3,
                           r: int = 1,
                           v: int = 1):
    """
    膨胀卷积核中心在指定坐标center处时，统计哪些像素被利用到，
    并在利用到的像素位置处加上增量v
    Args:
        center: 膨胀卷积核中心的坐标
        feature_map: 记录每个像素使用次数的特征图
        k: 膨胀卷积核的kernel大小
        r: 膨胀卷积的dilation rate
        v: 使用次数增量
    """
    assert divmod(3, 2)[1] == 1

    # left-top: (x, y)
    left_top = (center[0] - ((k - 1) // 2) * r, center[1] - ((k - 1) // 2) * r)
    for i in range(k):
        for j in range(k):
            feature_map[left_top[1] + i * r][left_top[0] + j * r] += v


def dilated_conv_all_map(dilated_map: np.ndarray,
                         k: int = 3,
                         r: int = 1):
    """
    根据输出特征矩阵中哪些像素被使用以及使用次数，
    配合膨胀卷积k和r计算输入特征矩阵哪些像素被使用以及使用次数
    Args:
        dilated_map: 记录输出特征矩阵中每个像素被使用次数的特征图
        k: 膨胀卷积核的kernel大小
        r: 膨胀卷积的dilation rate
    """
    new_map = np.zeros_like(dilated_map)
    for i in range(dilated_map.shape[0]):
        for j in range(dilated_map.shape[1]):
            if dilated_map[i][j] > 0:
                dilated_conv_one_pixel((j, i), new_map, k=k, r=r, v=dilated_map[i][j])

    return new_map


def plot_map(matrix: np.ndarray):
    plt.figure()

    c_list = ['white', 'blue', 'red']
    new_cmp = LinearSegmentedColormap.from_list('chaos', c_list)
    plt.imshow(matrix, cmap=new_cmp)

    ax = plt.gca()
    ax.set_xticks(np.arange(-0.5, matrix.shape[1], 1), minor=True)
    ax.set_yticks(np.arange(-0.5, matrix.shape[0], 1), minor=True)

    # 显示color bar
    plt.colorbar()

    # 在图中标注数量
    thresh = 5
    for x in range(matrix.shape[1]):
        for y in range(matrix.shape[0]):
            # 注意这里的matrix[y, x]不是matrix[x, y]
            info = int(matrix[y, x])
            ax.text(x, y, info,
                    verticalalignment='center',
                    horizontalalignment='center',
                    color="white" if info > thresh else "black")
    ax.grid(which='minor', color='black', linestyle='-', linewidth=1.5)
    plt.show()
    plt.close()


def main():
    # bottom to top
    dilated_rates = [1, 2, 3] # 修改此处的系数获得不同的实验结果
    # init feature map
    size = 31
    m = np.zeros(shape=(size, size), dtype=np.int32)
    center = size // 2
    m[center][center] = 1
    # print(m)
    # plot_map(m)

    for index, dilated_r in enumerate(dilated_rates[::-1]):
        new_map = dilated_conv_all_map(m, r=dilated_r)
        m = new_map
    print(m)
    plot_map(m)


if __name__ == '__main__':
    main()
    

• 上一节中例子1：r = [1, 2, 5] 的结果如下所示：
  
• 上一节中例子1：r = [1, 2, 9] 的结果如下所示：
  

---

总结

转置卷积参考-1
转置卷积参考-2
膨胀卷积参考