6.吴恩达深度学习--深度卷积模型:案例研究
本文主要参考了 严宽 大神的学习笔记,并在其基础上补充了一点内容,点此查看原文。
一、Keras入门-笑脸识别
本次我们将:
- 学习到一个高级的神经网络的框架
- 看看如何在几个小时内建立一个深入的学习算法
Keras 是为了使深度学习工程师能够很快地建立和实验不同的模型的框架,正如TensorFlow是一个比Python更高级的框架,Keras是一个更高层次的框架,并提供了额外的抽象方法。最关键的是Keras能够以最短的时间让想法变为现实。然而,Keras比底层框架更具有限制性,所以有一些非常复杂的模型可以在TensorFlow中实现,但在Keras中却没有(没有更多困难)。 话虽如此,Keras对许多常见模型都能正常运行。
import numpy as np
from keras import layers
from keras.layers import Input, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D
from keras.layers import AveragePooling2D, MaxPooling2D, Dropout, GlobalMaxPooling2D, GlobalAveragePooling2D
from keras.models import Model
from keras.preprocessing import image
from keras.utils import layer_utils
from keras.utils.data_utils import get_file
from keras.applications.imagenet_utils import preprocess_input
import pydot
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
from keras.utils.vis_utils import plot_model
import kt_utils
import keras.backend as K
K.set_image_data_format('channels_last')
import matplotlib.pyplot as plt
from matplotlib.pyplot import imshow
%matplotlib inline
1. 任务描述
下一次放假的时候,你决定和你的五个朋友一起度过一个星期。这是一个非常好的房子,在附近有很多事情要做,但最重要的好处是每个人在家里都会感到快乐,所以任何想进入房子的人都必须证明他们目前的幸福状态。
作为一个深度学习的专家,为了确保“快乐才开门”规则得到严格的应用,你将建立一个算法,它使用来自前门摄像头的图片来检查这个人是否快乐,只有在人高兴的时候,门才会打开。
你收集了你的朋友和你自己的照片,被前门的摄像头拍了下来。数据集已经标记好了。

2. 加载数据集
# 加载数据集
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = kt_utils.load_dataset()
# 归一化图片向量
X_train = X_train_orig / 255
X_test = X_test_orig / 255
# reshape
Y_train = Y_train_orig. T
Y_test = Y_test_orig.T
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
数据集的详细情况如下:
number of training examples = 600
number of test examples = 150
X_train shape: (600, 64, 64, 3)
Y_train shape: (600, 1)
X_test shape: (150, 64, 64, 3)
Y_test shape: (150, 1)
3. 使用 Keras 框架构建模型
Keras 非常适合快速搭建模型,它可以在很短的时间内建立一个很优秀的模型,模型框架代码如下:
def model(input_shape):
# 1.定义一个 tensor 的 placeholder,维度为 input_shape
X_input = Input(input_shape) # 输入层
# 2.使用 0 填充:X_input 的周围填充 0
X = ZeroPadding2D((3, 3))(X_input) # 上下左右分别填充 3 个0
# 3.对 X 使用 Conv -> BN -> ReLU块
X = Conv2D(32, (7, 7), strides=(1,1), name='conv0')(X) # 32个卷积核
X = BatchNormalization(axis = 3, name='bn0')(X)
X = Activation('relu')(X)
# 4.最大值池化层
X = MaxPooling2D((2, 2), name="max_pool")(X)
# 5.降维,矩阵转化为向量 + 全连接层
X = Flatten()(X)
X = Dense(1, activation='sigmoid', name='fc')(X)
# 创建模型,创建一个模型的实体,我们可以用它来训练、测试
model = Model(inputs = X_input, outputs = X, name = "HappyModel")
return model
根据上述模型框架代码,搭建自己想要的神经网络模型:
# 搭建的模型
def HappyModel(input_shape):
"""
实现一个检测笑容的模型
参数:
input_shape - 输入的数据的维度
返回:
model - 创建的Keras的模型
"""
X_input = Input(input_shape) # 输入层
# 这里用(3, 3)填充0是为了使得第一次卷积后维度不变
X = ZeroPadding2D((3, 3))(X_input)
X = Conv2D(32, (7, 7), strides=(1,1), name='conv0')(X) # 32个卷积核
X = BatchNormalization(axis = 3, name='bn0')(X)
X = Activation('relu')(X)
X = MaxPooling2D((2, 2), name="max_pool")(X)
X = Flatten()(X)
X = Dense(1, activation='sigmoid', name='fc')(X)
model = Model(inputs = X_input, outputs = X, name = "HappyModel")
return model
4. 训练模型
现在我们已经设计好了一个神经网络模型了,训练并测试模型的步骤如下:
- 创建一个模型实体
- 编译模型:
model.compile(optimizer = "...", loss = "...", metrics = ["accuracy"]) - 训练模型:
model.fit(x = ..., y = ..., epochs = ..., batch_size = ...) - 评估模型:
model.evaluate(x = ..., y = ...)
# 1.创建一个模型实体
happy_model = HappyModel(X_train.shape[1:]) # X_train.shape[1:]=(64, 64, 1)
# 2.编译模型
happy_model.compile("adam", "binary_crossentropy", metrics=['accuracy'])
# 3.训练模型
happy_model.fit(X_train, Y_train, epochs=40, batch_size=50)
# 4.评估模型
## verbose=1:输出日志记录
preds = happy_model.evaluate(X_test, Y_test, batch_size=32, verbose=1, sample_weight=None)
print ("误差值 = " + str(preds[0])) # 误差值 = 0.09271754910548528
print ("准确度 = " + str(preds[1])) # 准确度 = 0.96
import matplotlib.pyplot as plt
# 绘制训练准确率
plt.plot(history.history['acc'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.show()
# 绘制损失值
plt.plot(history.history['loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.show()
5. 预测
现在我们已经将模型训练好了,接下来我们用自己的图片进行测试
img = image.load_img('../data/my_image.jpg', target_size=(64, 64))
imshow(img)
print(img)
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = preprocess_input(x)
print(happy_model.predict(x))
6. 分析
打印模型每一层的细节:
happy_model.summary()
二、残差网络的搭建
这里我们将学习怎样使用残差网络构建一个非常深的卷积网络。理论上越深的网络越能实现复杂的功能,但是在实际上却难以训练,残差网络就是为了解决深层网络难以训练的问题的。
在本章节中,我们将完成下面两个认为:
- 实现基本的残差块
- 利用残差块实现并训练用于图像分类的神经网络
在解决问题前,我们先导入库函数:
import numpy as np
import tensorflow as tf
from keras import layers
from keras.layers import Input, Add, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D, AveragePooling2D, MaxPooling2D, GlobalMaxPooling2D
from keras.models import Model, load_model
from keras.preprocessing import image
from keras.utils import layer_utils
from keras.utils.data_utils import get_file
from keras.applications.imagenet_utils import preprocess_input
from keras.utils.vis_utils import model_to_dot
from keras.utils.vis_utils import plot_model
from keras.initializers import glorot_uniform
import pydot
from IPython.display import SVG
import scipy.misc
from matplotlib.pyplot import imshow
import keras.backend as K
K.set_image_data_format('channels_last')
K.set_learning_phase(1)
import resnets_utils
1. 深层网络的麻烦
使用深层网络最大的好处就是它能够完成很复杂的功能,它能够从边缘(浅层)到非常复杂的特征(深层)中不同的抽象层次的特征中学习。然而,使用比较深的网络通常没有什么好处,一个特别大的麻烦就在于训练的时候会产生梯度消失,非常深的网络通常会有一个梯度信号,该信号会迅速的消退,从而使得梯度下降变得非常缓慢。更具体的说,在梯度下降的过程中,当你从最后一层回到第一层的时候,你在每个步骤上乘以权重矩阵,因此梯度值可以迅速的指数式地减少到0(在极少数的情况下会迅速增长,造成梯度爆炸)。
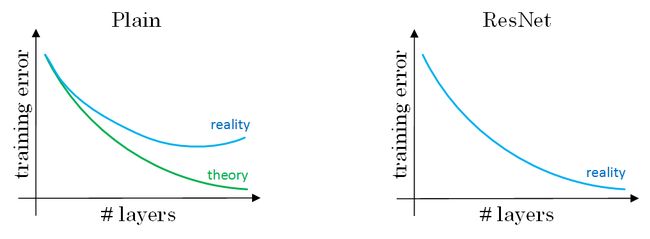
在训练的过程中,你可能会看到开始几层的梯度的大小(或范数)迅速下降到0,如下图:
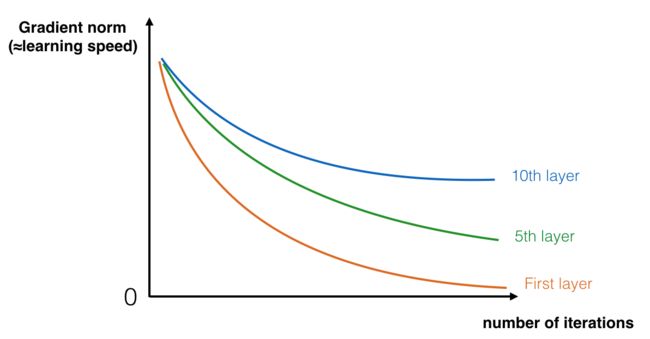
可以看到,随着迭代次数的增加,学习速度会下降的非常快,为了解决这个问题,我们将构建残差网络。
为什么残差网络能有效解决梯度消失的问题呢?
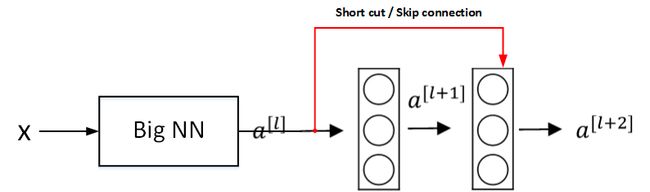
如上图所示,输入 X X X 经过很多层神经网络后输出 a [ l ] a^{[l]} a[l], a [ l ] a^{[l]} a[l] 经过一个 Residual block 输出 a [ l + 2 ] a^{[l+2]} a[l+2]。 a [ l + 2 ] a^{[l+2]} a[l+2] 的表达式为: a [ l + 2 ] = g ( z [ l + 2 ] + a [ l ] ) = g ( W [ l ] a [ l + 2 ] + b [ l ] + a [ l ] ) a^{[l+2]}=g(z^{[l+2]}+a^{[l]})=g(W^{[l]}a^{[l+2]}+b^{[l]}+a^{[l]}) a[l+2]=g(z[l+2]+a[l])=g(W[l]a[l+2]+b[l]+a[l])输入 X X X 经过 Big NN 后,若 W [ l + 2 ] ≈ 0 , b [ l + 2 ] ≈ 0 W^{[l+2]}\approx0,\ \ b^{[l+2]}\approx0 W[l+2]≈0, b[l+2]≈0,则有: a [ l + 2 ] = g ( a [ l ] ) = R e L U ( a [ l ] ) = a [ l ] w h e n a [ l ] ≥ 0 a^{[l+2]}=g(a^{[l]})=ReLU(a^{[l]})=a^{[l]}\ \ \ \ \ when\ \ a^{[l]}\geq0 a[l+2]=g(a[l])=ReLU(a[l])=a[l] when a[l]≥0可以看出,即使发生了梯度消失, W [ l + 2 ] ≈ 0 , b [ l + 2 ] ≈ 0 W^{[l+2]}\approx0,\ \ b^{[l+2]}\approx0 W[l+2]≈0, b[l+2]≈0,也能直接建立 a [ l + 2 ] a^{[l+2]} a[l+2] 和 a [ l ] a^{[l]} a[l] 的线性关系,且 a [ l + 2 ] = a [ l ] a^{[l+2]} = a^{[l]} a[l+2]=a[l],这其实就是identity function。 a [ l ] a^{[l]} a[l] 直接连接到 a [ l + 2 ] a^{[l+2]} a[l+2],从效果来说,相当于直接忽略了 a [ l ] a^{[l]} a[l] 之后的这两层神经层。这样,看似很深的神经网络,由于许多 Residual blocks 的存在,弱化削减了某些神经层之间的联系,实现隔层线性传递,而不是一味追求非线性关系,模型本身也就能“容忍”更深层的神经网络了。而且从性能上来说,这两层额外的 Residual blocks 也不会降低 Big NN 的性能。
当然,如果Residual blocks确实能训练得到非线性关系,那么也会忽略 short cut,跟 Plain Network 起到同样的效果。
有一点需要注意的是,如果 Residual blocks 中 a [ l ] a^{[l]} a[l] 和 a [ l + 2 ] a^{[l+2]} a[l+2] 的维度不同,通常可以引入矩阵 W s W_s Ws,与 a [ l ] a^{[l]} a[l] 相乘,使得 W s × a [ l ] W_s\times a^{[l]} Ws×a[l] 的维度与 a [ l + 2 ] a^{[l+2]} a[l+2] 的维度一致。参数矩阵 W s W_s Ws 有两种方法得到:一种是将 W s W_s Ws 为学习参数,通过模型训练得到;另一种是固定 W s W_s Ws 值(类似单位矩阵),不需要训练, W s × a [ l ] W_s\times a^{[l]} Ws×a[l] 仅仅使得 a [ l ] a^{[l]} a[l] 截断或者补零。这两种方法都可行。
2. 构建一个残差网络
在残差网络中,一个“捷径(shortcut)”或者说“跳跃连接(skip connection)”允许梯度直接反向传播到更浅的层,如下图:

图像左边是神经网络的主路,图像右边是添加了一条捷径的主路,通过这些残差块堆叠在一起,可以形成一个非常深的网络。
我们在视频中可以看到使用捷径的方式使得每一个残差块能够很容易学习到恒等式功能,这意味着我们可以添加很多的残差块而不会损害训练集的表现。
残差块有两种类型,主要取决于输入输出的维度是否相同,下面我们来看看吧~
1. 恒等块(Identity block)
恒等块是残差网络使用的的标准块,对应于输入的激活值(比如 a [ l ] a^{[l]} a[l] )与输出激活值(比如 a [ l + 1 ] a^{[l+1]} a[l+1])具有相同的维度。为了具象化残差块的不同步骤,我们来看看下面的图吧~
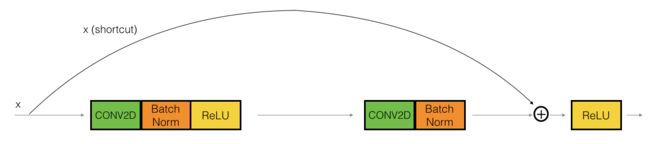
上图中,上面的曲线路径是捷径,下面的直线路径是主路径。在上图中,我们依旧把 CONV2D 与 ReLU 包含到了每个步骤中,为了提升训练的速度,我们在每一步也把数据进行了归一化(BatchNorm),不要害怕这些东西,因为 Keras 框架已经实现了这些东西,调用 BatchNorm 只需要一行代码。
在实践中,我们要做一个更强大的版本:跳跃连接会跳过3个隐藏层而不是两个,就像下图:
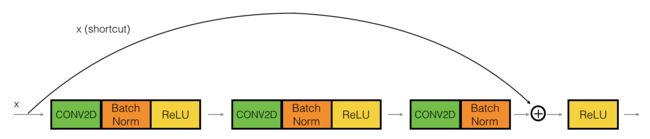
步骤如下:
- 主路径的第一部分:
① 第一个 Conv2D 有F1个过滤器,其大小为 (1, 1),步长为 (1, 1),使用填充方式为valid,命名规则为conv_name_base + '2a',使用 0 作为随机种子为其初始化。
② 第一个 BN 是对通道的轴进行归一化,其命名规则为bn_name_base + '2a'。
③ 使用 ReLU 激活函数 - 主路径的第二部分:
① 第二个 Conv2D 有F2个过滤器,其大小为 (f, f),步长为 (1, 1),使用填充方式为same,命名规则为conv_name_base + '2b',使用 0 作为随机种子为其初始化。
② 第二个 BN 是对通道的轴进行归一化,其命名规则为bn_name_base + '2b'。
③ 使用 ReLU 激活函数 - 主路径的第三部分:
① 第三个 Conv2D 有F3个过滤器,其大小为 (1, 1),步长为 (1, 1),使用填充方式为valid,命名规则为conv_name_base + '2c,使用 0 作为随机种子为其初始化。
② 第三个 BN 是对通道的轴进行归一化,其命名规则为bn_name_base + '2c'。
③ 注意这里没有使用 ReLU 激活函数 - 最后一步
① 将捷径与输入加在一起。
② 使用 ReLU 激活函数。
知道上述步骤之后,我们就开始动手实现残差块了:
def identity_block(X, f, filters, stage, block):
"""
实现图3的恒等块
参数:
X - 输入的tensor类型的数据,维度为( m, n_H_prev, n_W_prev, n_H_prev )
f - 整数,指定主路径中间的CONV窗口的维度
filters - 整数列表,定义了主路径每层的卷积层的过滤器数量
stage - 整数,根据每层的位置来命名每一层,与block参数一起使用。
block - 字符串,据每层的位置来命名每一层,与stage参数一起使用。
返回:
X - 恒等块的输出,tensor类型,维度为(n_H, n_W, n_C)
"""
# 定义命名规则
conv_name_base = "res" + str(stage) + block + "_branch"
bn_name_base = "bn" + str(stage) + block + "_branch"
# 获取过滤器
F1, F2, F3 = filters
# 保存输入数据,将会用于为主路径添加捷径
X_shortcut = X
# 主路径的第一部分
## 卷积层
### padding="valid":直接从原始图像的首段开始卷积,到最后不能匹配卷积核的部分直接舍去
X = Conv2D(filters=F1, kernel_size=(1, 1), strides=(1, 1), padding="valid",
name=conv_name_base + "2a", kernel_initializer=glorot_uniform(seed=0))(X)
## 归一化
X = BatchNormalization(axis=3, name=bn_name_base+"2a")(X)
## 使用 ReLU 激活函数
X = Activation("relu")(X)
# 主路径的第二部分
## 卷积层
X = Conv2D(filters=F2, kernel_size=(f,f),strides=(1,1), padding="same",
name=conv_name_base+"2b", kernel_initializer=glorot_uniform(seed=0))(X)
## 归一化
X = BatchNormalization(axis=3, name=bn_name_base+"2b")(X)
## 使用 ReLU 激活函数
X = Activation("relu")(X)
# 主路径的第三部分
## 卷积层
X = Conv2D(filters=F3, kernel_size=(1,1),strides=(1,1), padding="same",
name=conv_name_base+"2c", kernel_initializer=glorot_uniform(seed=0))(X)
## 归一化
X = BatchNormalization(axis=3, name=bn_name_base+"2c")(X)
## 没有 ReLU 激活函数
# 最后一步
## 将捷径与输入加在一起
X = Add()([X, X_shortcut])
## 使用 ReLU 激活函数
X = Activation("relu")(X)
return X
测试:
tf.compat.v1.disable_v2_behavior()
tf.compat.v1.reset_default_graph()
with tf.compat.v1.Session() as test:
np.random.seed(1)
A_prev = tf.compat.v1.placeholder("float", [3, 4, 4, 6])
X = np.random.randn(3, 4, 4, 6)
A = identity_block(A_prev, f=2, filters=[2, 4, 6], stage=1, block="a")
test.run(tf.compat.v1.global_variables_initializer()) # 参数初始化
out = test.run([A], feed_dict={A_prev:X, K.learning_phase():0}) # K.learning_phase():0 训练模式
print("out = " + str(out[0][1][1][0]))
test.close()
输出结果如下:
out = [0. 0. 1.3454674 2.0318177 0. 1.3246754]
2. 卷积块(Convolutional block)
我们已经实现了残差网络的恒等块,现在,残差网络的卷积块是另一种类型的残差块,它适用于输入输出的维度不一致的情况,它不同于上面的恒等块,与之区别在于,捷径中有一个 CONV2D 层,如下图:
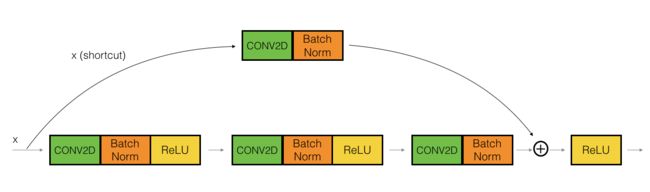
捷径中的卷积层将把输入 X X X 卷积为不同的维度,因此在主路径最后那里需要适配捷径中的维度。比如:把激活值中的宽高减少 2 倍,我们可以使用 1 × 1 1\times1 1×1 的卷积,步伐为 2。捷径上的卷积层不使用任何非线性激活函数,它的主要作用是仅仅应用(学习后的)线性函数来减少输入的维度,以便在后面的加法步骤中的维度相匹配。
具体步骤如下:
- 主路径的第一部分:
① 第一个 Conv2D 有F1个过滤器,其大小为 (1, 1),步长为 (s, s),使用填充方式为valid,命名规则为conv_name_base + '2a',使用 0 作为随机种子为其初始化。
② 第一个 BN 是对通道的轴进行归一化,其命名规则为bn_name_base + '2a'。
③ 使用 ReLU 激活函数 - 主路径的第二部分:
① 第二个 Conv2D 有F2个过滤器,其大小为 (f, f),步长为 (1, 1),使用填充方式为same,命名规则为conv_name_base + '2b',使用 0 作为随机种子为其初始化。
② 第二个 BN 是对通道的轴进行归一化,其命名规则为bn_name_base + '2b'。
③ 使用 ReLU 激活函数 - 主路径的第三部分:
① 第三个 Conv2D 有F3个过滤器,其大小为 (1, 1),步长为 (1, 1),使用填充方式为valid,命名规则为conv_name_base + '2c,使用 0 作为随机种子为其初始化。
② 第三个 BN 是对通道的轴进行归一化,其命名规则为bn_name_base + '2c'。
③ 注意这里没有使用 ReLU 激活函数 - 最后一步
① 此卷积层有F3个过滤器,其大小为 (1, 1),步长为 (s, s),使用填充方式为valid,命名规则为conv_name_base + '1'
② BN 是对通道的轴进行归一化,其命名规则为bn_name_base + '1'。 - 最后一步
① 将捷径与输入加在一起。
② 使用 ReLU 激活函数。
def convolutional_block(X, f, filters, stage, block, s=2):
"""
实现图5的卷积块
参数:
X - 输入的tensor类型的变量,维度为( m, n_H_prev, n_W_prev, n_C_prev)
f - 整数,指定主路径中间的CONV窗口的维度
filters - 整数列表,定义了主路径每层的卷积层的过滤器数量
stage - 整数,根据每层的位置来命名每一层,与block参数一起使用。
block - 字符串,据每层的位置来命名每一层,与stage参数一起使用。
s - 整数,指定要使用的步幅
返回:
X - 卷积块的输出,tensor类型,维度为(n_H, n_W, n_C)
"""
#定义命名规则
conv_name_base = "res" + str(stage) + block + "_branch"
bn_name_base = "bn" + str(stage) + block + "_branch"
#获取过滤器数量
F1, F2, F3 = filters
#保存输入数据
X_shortcut = X
#主路径
##主路径第一部分
X = Conv2D(filters=F1, kernel_size=(1,1), strides=(s,s), padding="valid",
name=conv_name_base+"2a", kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3,name=bn_name_base+"2a")(X)
X = Activation("relu")(X)
##主路径第二部分
X = Conv2D(filters=F2, kernel_size=(f,f), strides=(1,1), padding="same",
name=conv_name_base+"2b", kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3,name=bn_name_base+"2b")(X)
X = Activation("relu")(X)
##主路径第三部分
X = Conv2D(filters=F3, kernel_size=(1,1), strides=(1,1), padding="valid",
name=conv_name_base+"2c", kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3,name=bn_name_base+"2c")(X)
#捷径
X_shortcut = Conv2D(filters=F3, kernel_size=(1,1), strides=(s,s), padding="valid",
name=conv_name_base+"1", kernel_initializer=glorot_uniform(seed=0))(X_shortcut)
X_shortcut = BatchNormalization(axis=3,name=bn_name_base+"1")(X_shortcut)
#最后一步
X = Add()([X,X_shortcut])
X = Activation("relu")(X)
return X
测试:
tf.compat.v1.disable_v2_behavior()
tf.compat.v1.reset_default_graph()
with tf.compat.v1.Session() as test:
np.random.seed(1)
A_prev = tf.compat.v1.placeholder("float", [3, 4, 4, 6])
X = np.random.randn(3, 4, 4, 6)
A = identity_block(A_prev, f=2, filters=[2, 4, 6], stage=1, block="a")
# K.learning_phase():决定当前模型执行于训练模式下(1)还是测试模式下(0).
test.run(tf.compat.v1.global_variables_initializer())
out = test.run([A], feed_dict={A_prev:X, K.learning_phase():0})
print("out = " + str(out[0][1][1][0]))
test.close()
测试结果如下:
out = [0. 0. 1.3454674 2.0318177 0. 1.3246754]
3. 构建一个深层残差网络
我们已经做完所需要的所有残差块了,下面这个图就描述了神经网络的算法细节,图中的 ID BLOCK 是指标准的恒等块,ID BLOCK x3 是指把三个恒等块放在一起。
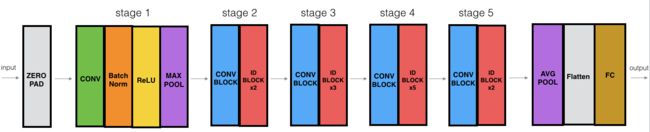
这个深层网络的具体细节如下:
- 对输入数据进行0填充,padding =(3,3)
- stage 1:
① 卷积层有64个过滤器,其维度为(7,7),步伐为(2,2),命名为“conv1”
② 规范层(BatchNorm)对输入数据进行通道轴归一化
③ 最大值池化层使用一个(3,3)的窗口和(2,2)的步伐 - stage 2:
① 卷积块使用f=3个大小为[64,64,256]的过滤器,f=3,s=1,block=“a”
② 2个恒等块使用三个大小为[64,64,256]的过滤器,f=3,block=“b”、“c” - stage 3
① 卷积块使用f=3个大小为[128,128,512]的过滤器,f=3,s=2,block=“a”
② 3个恒等块使用三个大小为[128,128,512]的过滤器,f=3,block=“b”、“c”、“d” - stage 4
① 卷积块使用f=3个大小为[256,256,1024]的过滤器,f=3,s=2,block=“a”
② 5个恒等块使用三个大小为[256,256,1024]的过滤器,f=3,block=“b”、“c”、“d”、“e”、“f” - stage 5
① 卷积块使用f=3个大小为[512,512,2048]的过滤器,f=3,s=2,block=“a”
② 2个恒等块使用三个大小为[256,256,2048]的过滤器,f=3,block=“b”、“c” - 均值池化层使用维度为(2,2)的窗口,命名为“avg_pool”
- 展开操作没有任何超参数以及命名
- 全连接层(密集连接)使用softmax激活函数,命名为
"fc" + str(classes)
根据上述网络结构构建模型,这里在第一层卷积层和最后一个全连接层做了 L1 正则化,这样大大的提高了模型的准确率。
def ResNet_deep(input_shape=(64, 64, 3), classes=6):
"""
实现ResNet50
CONV2D -> BATCHNORM -> RELU -> MAXPOOL -> CONVBLOCK -> IDBLOCK*2 -> CONVBLOCK -> IDBLOCK*3
-> CONVBLOCK -> IDBLOCK*5 -> CONVBLOCK -> IDBLOCK*2 -> AVGPOOL -> TOPLAYER
参数:
input_shape - 图像数据集的维度
classes - 整数,分类数
返回:
model - Keras框架的模型
"""
# 定义一个 tensor 的 placeholder,维度为 input_shape
X_input = Input(input_shape) # 输入层
# 使用 0 填充:X_input 的周围填充 0
X = ZeroPadding2D((3, 3))(X_input) # 上下左右分别填充 3 个0
# stage1
X = Conv2D(64, (7, 7), strides=(2,2), name='conv1',
kernel_regularizer=regularizers.l1(0.01),
kernel_initializer=glorot_uniform(seed=0))(X) # 64个卷积核
X = BatchNormalization(axis = 3, name='bn_conv1')(X)
X = Activation('relu')(X)
X = MaxPooling2D((2, 2), name="max_pool")(X)
# stage2
X = convolutional_block(X, f=3, filters=[64, 64, 256], stage=2, block="a", s=1)
X = identity_block(X, f=3, filters=[64, 64, 256], stage=2, block="b")
X = identity_block(X, f=3, filters=[64, 64, 256], stage=2, block="c")
# stage3
X = convolutional_block(X, f=3, filters=[128, 128, 512], stage=3, block="a", s=2)
X = identity_block(X, f=3, filters=[128, 128, 512], stage=3, block="b")
X = identity_block(X, f=3, filters=[128, 128, 512], stage=3, block="c")
X = identity_block(X, f=3, filters=[128, 128, 512], stage=3, block="d")
# stage4
X = convolutional_block(X, f=3, filters=[256, 256, 1024], stage=4, block="a", s=2)
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="b")
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="c")
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="d")
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="e")
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="f")
# stage5
X = convolutional_block(X, f=3, filters=[512, 512, 2048], stage=5, block="a", s=2)
X = identity_block(X, f=3, filters=[512, 512, 2048], stage=5, block="b")
X = identity_block(X, f=3, filters=[512, 512, 2048], stage=5, block="c")
# 均值池化层
X = AveragePooling2D(pool_size=(2, 2), padding="same")(X)
# 降维,矩阵转化为向量 + 全连接层
X = Flatten()(X)
## classes:输出的维度
X = Dense(classes, kernel_regularizer=regularizers.l1(0.01), # 加入正则化项
activation='softmax', name="fc"+str(classes),
kernel_initializer=glorot_uniform(seed=0))(X)
# 创建模型,创建一个模型的实体,我们可以用它来训练、测试
model = Model(inputs = X_input, outputs = X, name = "ResNet50")
return model
编译模型:
model = ResNet_deep(input_shape=(64, 64, 3), classes=6)
model.compile(optimizer="adam", loss="categorical_crossentropy", metrics=["accuracy"])
加载数据集:
# 加载手势数据集
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = resnets_utils.load_dataset()
# Normalize image vectors
X_train = X_train_orig / 255.
X_test = X_test_orig / 255.
# Convert training and test labels to one hot matrices
Y_train = resnets_utils.convert_to_one_hot(Y_train_orig, 6).T
Y_test = resnets_utils.convert_to_one_hot(Y_test_orig, 6).T
print("number of training examples = " + str(X_train.shape[0]))
print("number of test examples = " + str(X_test.shape[0]))
print("X_train shape: " + str(X_train.shape))
print("Y_train shape: " + str(Y_train.shape))
print("X_test shape: " + str(X_test.shape))
print("Y_test shape: " + str(Y_test.shape))
数据集信息如下:
number of training examples = 1080
number of test examples = 120
X_train shape: (1080, 64, 64, 3)
Y_train shape: (1080, 6)
X_test shape: (120, 64, 64, 3)
Y_test shape: (120, 6)
运行模型:
history = model.fit(X_train, Y_train, epochs=20, batch_size=32)
评估模型:
preds = model.evaluate(X_test, Y_test)
print("误差值 = " + str(preds[0]))
print("准确率 = " + str(preds[1]))
模型的误差值和准确率为:
误差值 = 1.0332518259684245
准确率 = 0.95
绘制准确率曲线:
import matplotlib.pyplot as plt
# 绘制训练准确率
plt.plot(history.history['acc'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.show()
用自己的图片做测试:
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt # plt 用于显示图片
import imageio
%matplotlib inline
img_path = '../data/my_finger.jpg'
my_image = image.load_img(img_path, target_size=(64, 64))
my_image = image.img_to_array(my_image)
my_image = np.expand_dims(my_image,axis=0)
my_image = preprocess_input(my_image)
print("my_image.shape = " + str(my_image.shape))
print("class prediction vector [p(0), p(1), p(2), p(3), p(4), p(5)] = ")
print(model.predict(my_image))
my_image = imageio.imread(img_path)
plt.imshow(my_image)
测试结果如下:
my_image.shape = (1, 64, 64, 3)
class prediction vector [p(0), p(1), p(2), p(3), p(4), p(5)] =
[[0.19364846 0.19265611 0.14671138 0.2302679 0.07059721 0.16611898]]
分析模型整体架构:
model.summary()