时间序列的数据分析(三):经典时间序列分解
之前已经完成了以前两篇博客,还没有阅读过的读者请先阅读:
-
时间序列的数据分析(一):主要成分
-
时间序列的数据分析(二):数据趋势的计算
五.时间序列分解
之前已经介绍过时间序列数据的季节性特征可以分为加法季节性和乘法季节性,因此对时间序列数据进行分解就会有加法分解和乘法分解两种方法。下面分别用手动方法和自动方法(调用statsmodes.seasonal_decompose)来实现分解,之所以要使用手动方法是为了让读者能彻底搞懂时间序列分解的内置逻辑。
5.1季节性周期的判断
时间序列的数据往往会呈现出周期性变化的规律,这种周期性变化规律往往是由季节性因素所带来的,如果您手上的时间序列数据的时间颗粒度是时刻(如小时),那它的季节性周期有可能是24,如果时间颗粒度是天,那季节性周期有可能是7,如果时间颗粒度是月,那季节性周期有可能是12,如果时间颗粒度是季度,那它的季节性周期有可能是4。下面我们查看一下国际航空公司人员数量的数据集的趋势图。
df=pd.read_csv("airline_Passengers.csv")
df['Period']=pd.to_datetime(df['Period'])
df.plot(x='Period',y='#Passengers',title="Airline passengers",figsize=(10,6));
xcoords = ['1950-01', '1951-01', '1952-01', '1953-01', '1954-01',
'1955-01', '1956-01', '1957-01', '1958-01', '1959-01-01','1960-01']
for xc in xcoords:
plt.axvline(x=xc, color='blue', linestyle='--')该数据集的时间范围从1949-1960共12年,时间颗粒度是月,即每月1条数据12年总共144条月度数据,因为一年有12个月,因此一般认为该数据集季节性周期为12,即每12个月数据会发生一次周期性波动,这一点从上图中各蓝色竖线范围内数据的变化规律可知(蓝色竖线位置为每年开始的位置),上图中数据每12个月发生周期性波动且每年的波动幅度会逐渐增加,这表现出乘法季节性的特征。
5.2加法分解(手动法)
步骤1: 计算趋势周期项
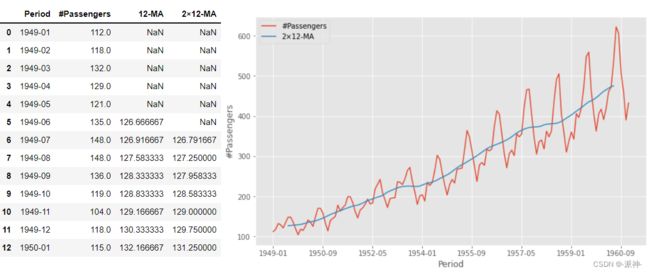
倘若季节性周期m为奇数时我们简单移动平均法来计算趋势周期项,即用 m-MA 来计算趋势周期项 ,若季节性周期m为偶数时用 2×m-MA 来计算趋势周期项,上面的例子中季节性周期为12为偶数所以需要用2×m-MA 来计算趋势周期项。
order=12
df[str(order)+'-MA']=df['#Passengers'].rolling(window=order,center=True).mean()
df['2×12-MA']=df[str(order)+'-MA'].rolling(window=2).mean()步骤2:计算去趋势序列
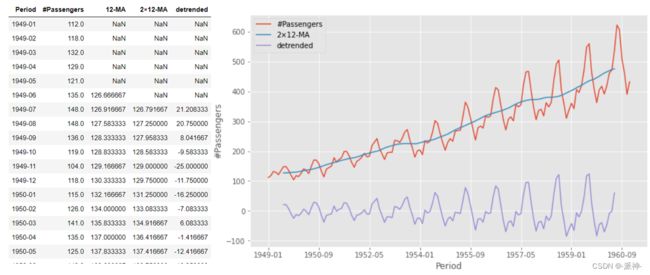
我们需要从原始数据集中删掉趋势的影响,即用#Passengers例减去2×12-MA列得到一个新列:detrended
df['detrended']=df['#Passengers']-df['2×12-MA']
df.plot(x='Period',
y=['#Passengers','2×12-MA','detrended'],
ylabel='#Passengers',figsize=(10,6));步骤3:计算季节项
计算季节项的基本思路是:1.根据数据的时间颗粒度(小时、天、月、季、年等)计算平均值(例如如果数据的时间颗粒度是月,那就计算每个月(1-12月)在所有年份的平均值),2.将这些平均值再减去去趋势值(detrended)的平均值, 3.将结果的数量进行扩展。
#记录条数
num_data=df.shape[0]
#季节性周期
period=12
#1.计算月度平均值
df['month']=df.Period.apply(lambda x:pd.to_datetime(x).month)
month_mean=df.groupby('month').detrended.mean().values
#2.月度均值减去趋势平均值
detrended_month_mean=month_mean-df.detrended.mean()
#3.扩展结果数量
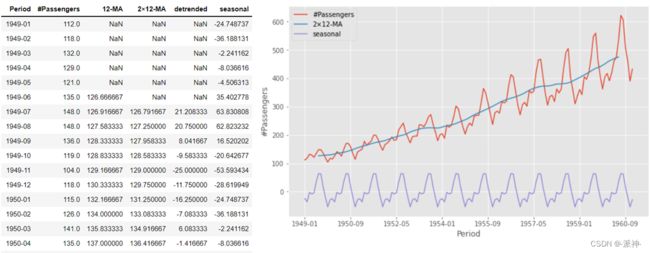
df['seasonal'] = np.tile(detrended_month_mean,num_data //period +1)[:num_data]
df=df.drop(['month'],axis=1)
df.plot(x='Period',
y=['#Passengers','2×12-MA','seasonal'],
ylabel='#Passengers',figsize=(10,6));步骤4:计算残差
残差的计算比较简单只要将去趋势值(detrended)减去季节项(seasonal)就可以得到残差:
#计算残差
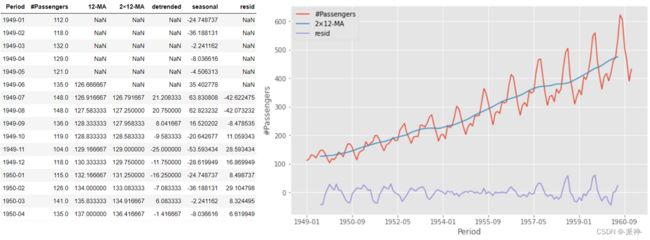
df['resid']=df.detrended-df.seasonal
df.plot(x='Period',
y=['#Passengers','2×12-MA','resid'],
ylabel='#Passengers',figsize=(10,6));最后把趋势、季节项、残差放在一起展示:
df['Period'] = pd.to_datetime(df['Period'])
plt.figure(figsize=(10,8))
plt.subplot(4,1,1)
plt.plot(df.Period.values,df['#Passengers'].values)
plt.ylabel('#Passengers');
plt.title('Additive Decomposition');
plt.subplot(4,1,2);
plt.plot(df.Period.values,df['2×12-MA'].values)
plt.ylabel('trend')
plt.subplot(4,1,3);
plt.plot(df.Period.values,df['seasonal'].values)
plt.ylabel('seasonal')
plt.subplot(4,1,4);
plt.scatter(df.Period.values,df['resid'].values)
plt.ylabel('resid');5.3乘法分解(手动法)
步骤1: 计算趋势周期项
与加法相同
步骤2:计算去趋势序列
将原始数据除以趋势,即用#Passengers例除以2×12-MA列得到一个新列:detrended
df['detrended']=df['#Passengers']/df['2×12-MA']步骤3:计算季节项
计算季节项的基本思路是:1.根据数据的时间颗粒度(小时、天、月、季、年等)计算平均值(例如如果数据的时间颗粒度是月,那就计算每个月(1-12月)在所有年份的平均值),2.将这些平均值再除以去趋势值(detrended)的平均值, 3.将结果的数量进行扩展。
#记录条数
num_data=df.shape[0]
#季节性周期
period=12
#1.计算月度平均值
df['month']=df.Period.apply(lambda x:pd.to_datetime(x).month)
month_mean=df.groupby('month').detrended.mean().values
#2.月度均值除以趋势平均值
detrended_month_mean=month_mean/df.detrended.mean()
#3.扩展结果数量
df['seasonal'] = np.tile(detrended_month_mean,num_data //period+1)[:num_data]
df=df.drop(['month'],axis=1) 步骤4:计算残差
残差的计算比较简单只要将去原始数据除以趋势和季节项的积就可以得到残差即: data/(trend*seasonal)
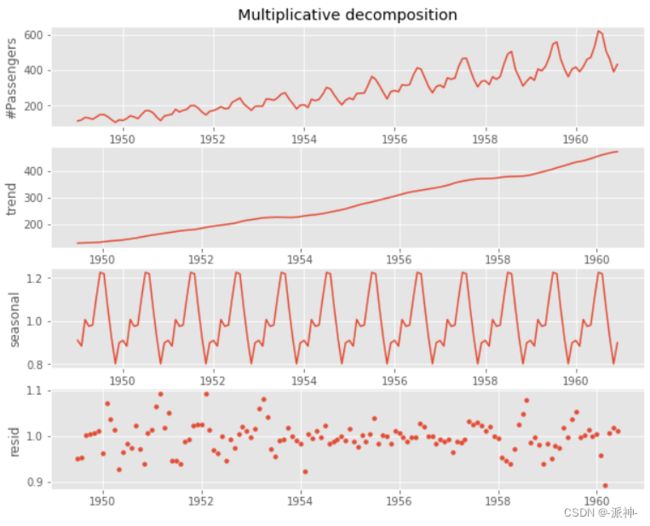
df['resid'] =df['#Passengers']/(df['2×12-MA']*df.seasonal)最后把趋势、季节项、残差放在一起展示:
df['Period'] = pd.to_datetime(df['Period'])
plt.figure(figsize=(10,8))
plt.subplot(4,1,1)
plt.plot(df.Period.values,df['#Passengers'].values)
plt.ylabel('#Passengers');
plt.title('Multiplicative decomposition');
plt.subplot(4,1,2);
plt.plot(df.Period.values,df['2×12-MA'].values)
plt.ylabel('trend')
plt.subplot(4,1,3);
plt.plot(df.Period.values,df['seasonal'].values)
plt.ylabel('seasonal')
plt.subplot(4,1,4);
plt.scatter(df.Period.values,df['resid'].values,s=15)
plt.ylabel('resid');5.3 使用statsmodels包来自动分解时间序列
下面我们使用statsmodels包来分解时间序列,我们会调用statsmodels的seasonal_decompose方法,并且通过设置参数mode="additive(multiplicative)"来执行加法(乘法)分解操作:
from statsmodels.tsa.seasonal import STL, seasonal_decompose
plt.rc("figure", figsize=(10, 6))
df=pd.read_csv("airline_Passengers.csv")
df.set_index('Period',inplace=True)
df.index = pd.to_datetime(df.index)
data = df["#Passengers"]
seasonal_decomp = seasonal_decompose(data, model="additive",period=12)
df['trend']=seasonal_decomp.trend
df['seasonal']=seasonal_decomp.seasonal
df['resid']=seasonal_decomp.resid
seasonal_decomp.plot();通过上图的数据结果中我们发现自动加法分解的结果与我们手动分解的结果是一致的。
总结
在本章中我们学习了时间序列数据的加法分解和乘法分解的基本步骤,我们一步步通过手动的方法计算了趋势、去趋势项、季节项、残差项等特征项,手动分解的目的是让读者能进一步了解各个特征项的计算逻辑,最后我们使用了statsmodels的seasonal_decompose方法来自动分解,并对比了手动分解与自动分解的结果,并确认他们是一致的。