简单聊聊模型的性能评估标准

机器学习入门系列（2）–如何构建一个完整的机器学习项目，第十篇！

该系列的前 9 篇文章：

• 机器学习入门系列(2)–如何构建一个完整的机器学习项目(一)
• 机器学习数据集的获取和测试集的构建方法
• 特征工程之数据预处理（上）
• 特征工程之数据预处理（下）
• 特征工程之特征缩放&特征编码
• 特征工程(完)
• 常用机器学习算法汇总比较(上）
• 常用机器学习算法汇总比较(中）
• 常用机器学习算法汇总比较(完）

这个系列的文章也是要开始进入尾声了，最后就主要是模型评估部分的内容了。

在机器学习领域中，对模型的评估非常重要，只有选择和问题相匹配的评估方法，才能快速发现算法模型或者训练过程的问题，迭代地对模型进行优化。

模型评估主要分为离线评估和在线评估两个阶段。并且针对分类、回归、排序、序列预测等不同类型的机器学习问题，评估指标的选择也有所不同。

模型评估这部分会介绍以下几方面的内容：

• 性能度量
• 模型评估方法
• 泛化能力
• 过拟合、欠拟合
• 超参数调优

本文会首先介绍性能度量方面的内容，主要是分类问题和回归问题的性能指标，包括以下几个方法的介绍：

• 准确率和错误率
• 精确率、召回率以及 F1
• ROC 曲线 和 AUC
• 代价矩阵
• 回归问题的性能度量
• 其他评价指标，如计算速度、鲁棒性等

1. 性能度量

性能度量就是指对模型泛化能力衡量的评价标准。

1.1 准确率和错误率

分类问题中最常用的两个性能度量标准–准确率和错误率。

准确率：指的是分类正确的样本数量占样本总数的比例，定义如下：
$$Accuracy=\frac{n_{correct}}{N}$$
错误率：指分类错误的样本占样本总数的比例，定义如下：
$$Error=\frac{n_{error}}{N}$$
错误率也是损失函数为 0-1 损失时的误差。

这两种评价标准是分类问题中最简单也是最直观的评价指标。但它们都存在一个问题，在类别不平衡的情况下，它们都无法有效评价模型的泛化能力。即如果此时有 99% 的负样本，那么模型预测所有样本都是负样本的时候，可以得到 99% 的准确率。

这种情况就是在类别不平衡的时候，占比大的类别往往成为影响准确率的最主要因素！

这种时候，其中一种解决方法就是更换评价指标，比如采用更为有效的平均准确率(每个类别的样本准确率的算术平均)，即：
$$A_{mean}=\frac{a_1+a_2+\cdots +a_m}{m}$$
其中 m 是类别的数量。

对于准确率和错误率，用 Python 代码实现如下图所示：

def accuracy(y_true, y_pred):
    return sum(y == y_p for y, y_p in zip(y_true, y_pred)) / len(y_true)

def error(y_true, y_pred):
    return sum(y != y_p for y, y_p in zip(y_true, y_pred)) / len(y_true)

一个简单的二分类测试样例：

y_true = [1, 0, 1, 0, 1]
y_pred = [0, 0, 1, 1, 0]

acc = accuracy(y_true, y_pred)
err = error(y_true, y_pred)
print('accuracy=', acc)
print('error=', err)

输出结果如下：

accuracy= 0.4
error= 0.6

1.2 精确率、召回率、P-R 曲线和 F1

1.2.1 精确率和召回率

精确率，也被称作查准率，是指所有预测为正类的结果中，真正的正类的比例。公式如下：
$$P=\frac{TP}{TP+FP}$$
召回率，也被称作查全率，是指所有正类中，被分类器找出来的比例。公式如下：
$$R=\frac{TP}{TP+FN}$$
对于上述两个公式的符号定义，是在二分类问题中，我们将关注的类别作为正类，其他类别作为负类别，因此，定义：

• TP(True Positive)：真正正类的数量，即分类为正类，实际也是正类的样本数量；
• FP(False Positive)：假正类的数量，即分类为正类，但实际是负类的样本数量；
• FN(False Negative)：假负类的数量，即分类为负类，但实际是正类的样本数量；
• TN(True Negative)：真负类的数量，即分类是负类，实际也负类的样本数量。

更形象的说明，可以参考下表，也是混淆矩阵的定义：

	预测：正类	预测：负类
实际：正类	TP	FN
实际：负类	FP	TN

精确率和召回率是一对矛盾的度量，通常精确率高时，召回率往往会比较低；而召回率高时，精确率则会比较低，原因如下：

• 精确率越高，代表预测为正类的比例更高，而要做到这点，通常就是只选择有把握的样本。最简单的就是只挑选最有把握的一个样本，此时 FP=0，P=1，但 FN 必然非常大(没把握的都判定为负类)，召回率就非常低了；
• 召回率要高，就是需要找到所有正类出来，要做到这点，最简单的就是所有类别都判定为正类，那么 FN=0 ，但 FP 也很大，所有精确率就很低了。

而且不同的问题，侧重的评价指标也不同，比如：

• 对于推荐系统，侧重的是精确率。也就是希望推荐的结果都是用户感兴趣的结果，即用户感兴趣的信息比例要高，因为通常给用户展示的窗口有限，一般只能展示 5 个，或者 10 个，所以更要求推荐给用户真正感兴趣的信息；
• 对于医学诊断系统，侧重的是召回率。即希望不漏检任何疾病患者，如果漏检了，就可能耽搁患者治疗，导致病情恶化。

精确率和召回率的代码简单实现如下，这是基于二分类的情况

def precision(y_true, y_pred):
    true_positive = sum(y and y_p for y, y_p in zip(y_true, y_pred))
    predicted_positive = sum(y_pred)
    return true_positive / predicted_positive
def recall(y_true, y_pred):
    true_positive = sum(y and y_p for y, y_p in zip(y_true, y_pred))
    real_positive = sum(y_true)
    return true_positive / real_positive

简单的测试样例以及输出如下

y_true = [1, 0, 1, 0, 1]
y_pred = [0, 0, 1, 1, 0]

precisions = precision(y_true, y_pred)
recalls = recall(y_true, y_pred)

print('precisions=', precisions) # 输出为0.5
print('recalls=', recalls)       # 输出为 0.3333

1.2.2 P-R 曲线和 F1

很多时候，我们都可以根据分类器的预测结果对样本进行排序，越靠前的是分类器越有把握是正类的样本，而最后面的自然就是分类器觉得最不可能是正类的样本了。

一般来说，这个预测结果其实就是分类器对样本判断为某个类别的置信度，我们可以选择不同的阈值来调整分类器对某个样本的输出结果，比如设置阈值是 0.9，那么只有置信度是大于等于 0.9 的样本才会最终判定为正类，其余的都是负类。

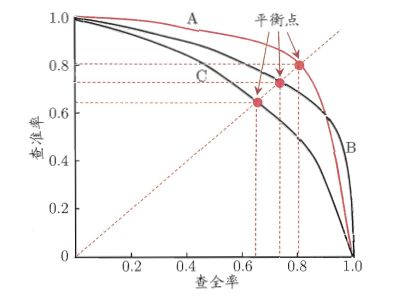
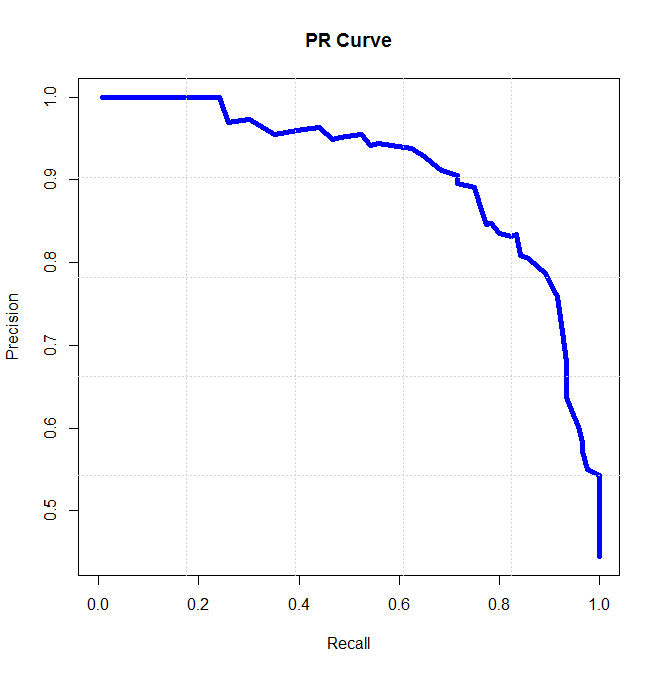
我们设置不同的阈值，自然就会得到不同的正类数量和负类数量，依次计算不同情况的精确率和召回率，然后我们可以以精确率为纵轴，召回率为横轴，绘制一条“P-R曲线”，如下图所示：

当然，以上这个曲线是比较理想情况下的，未来绘图方便和美观，实际情况如下图所示：

对于 P-R 曲线，有：

1.曲线从左上角 (0,1) 到右下角 (1,0) 的走势，正好反映了精确率和召回率是一对矛盾的度量，一个高另一个低的特点：

• 开始是精确率高，因为设置阈值很高，只有第一个样本（分类器最有把握是正类）被预测为正类，其他都是负类，所以精确率高，几乎是 1，而召回率几乎是 0，仅仅找到 1 个正类。
• 右下角时候就是召回率很高，精确率很低，此时设置阈值就是 0，所以类别都被预测为正类，所有正类都被找到了，召回率很高，而精确率非常低，因为大量负类被预测为正类。

2.P-R 曲线可以非常直观显示出分类器在样本总体上的精确率和召回率。所以可以对比两个分类器在同个测试集上的 P-R 曲线来比较它们的分类能力：

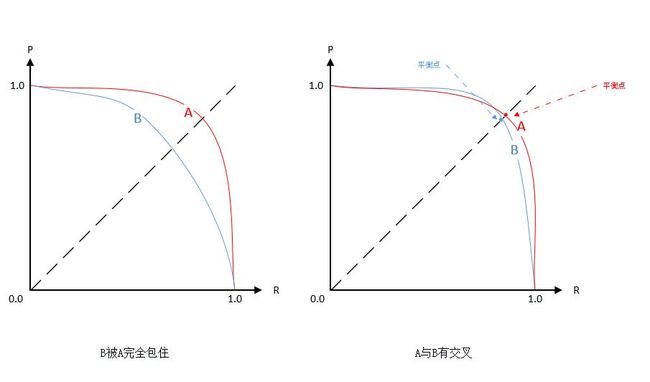
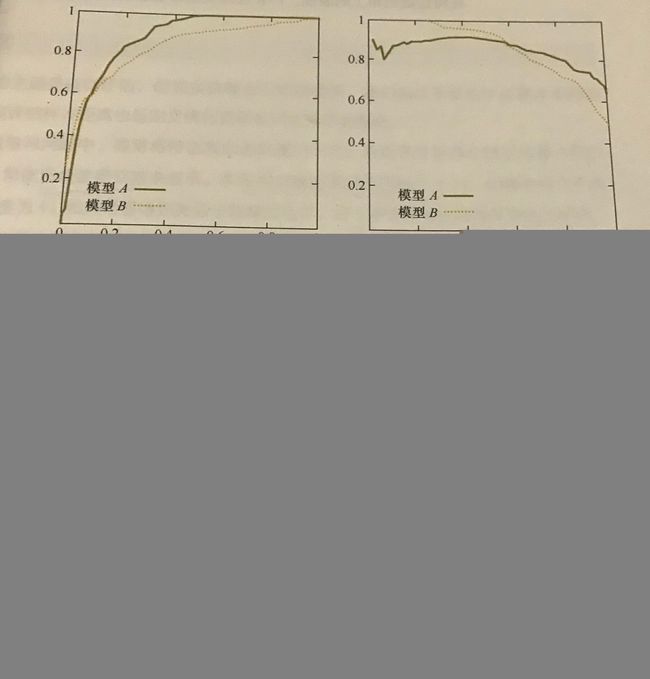
• 如果分类器 B 的 P-R 曲线被分类器 A 的曲线完全包住，如下左图所示，则可以说，A 的性能优于 B;
• 如果是下面的右图，两者的曲线有交叉，则很难直接判断两个分类器的优劣，只能根据具体的精确率和召回率进行比较：
  • 一个合理的依据是比较 P-R 曲线下方的面积大小，它在一定程度上表征了分类器在精确率和召回率上取得“双高”的比例，但这个数值不容易计算；
  • 另一个比较就是平衡点(Break-Event Point, BEP)，它是精确率等于召回率时的取值，如下右图所示，而且可以判定，平衡点较远的曲线更好。

当然了，平衡点还是过于简化，于是有了 F1 值这个新的评价标准，它是精确率和召回率的调和平均值，定义为：
$$F1=\frac{2\times P\times R}{P+R}=\frac{2\times TP}{样本总数+TP-TN}$$
F1 还有一个更一般的形式：$F_{\beta }$，能让我们表达出对精确率和召回率的不同偏好，定义如下：
$$F_{\beta }=\frac{(1+{\beta }^2)\times P\times R}{({\beta }^2\times P)+R}$$
其中$\beta >0$ 度量了召回率对精确率的相对重要性，当 $\beta =1$，就是 F1；如果 $\beta >1$，召回率更加重要；如果 $\beta <1$，则是精确率更加重要。

1.2.3 宏精确率/微精确率、宏召回率/微召回率以及宏 F1 / 微 F1

很多时候，我们会得到不止一个二分类的混淆矩阵，比如多次训练/测试得到多个混淆矩阵，在多个数据集上进行训练/测试来估计算法的“全局”性能，或者是执行多分类任务时对类别两两组合得到多个混淆矩阵。

总之，我们希望在 n 个二分类混淆矩阵上综合考察精确率和召回率。这里一般有两种方法来进行考察：

1.第一种是直接在各个混淆矩阵上分别计算出精确率和召回率，记为 $(P_1,R_1),(P_2,R_2),\cdots ,(P_n,R_n)$，接着计算平均值，就得到宏精确率(macro-P)、宏召回率(macro-R)以及宏 F1(macro-F1) , 定义如下：
$$\begin{gathered} macro-P=\frac{1}{n}\sum _{i=1}^n{P}_i, \\ macro-R=\frac{1}{n}\sum _{i=1}^n{R}_i, \\ macro-F1=\frac{2\times macro-P\times macro-R}{marco-P+macro-R} \end{gathered}$$
2.第二种则是对每个混淆矩阵的对应元素进行平均，得到 TP、FP、TN、FN 的平均值，再基于这些平均值就就得到微精确率(micro-P)、微召回率(micro-R)以及微 F1(micro-F1) , 定义如下：
$$\begin{gathered} micro-P=\frac{\overline{TP}}{\overline{TP}+\overline{FP}}, \\ micro-R=\frac{\overline{TP}}{\overline{TP}+\overline{FN}}, \\ micro-F1=\frac{2\times micro-P\times micro-R}{micro-P+micro-R} \end{gathered}$$

1.3 ROC 与 AUC

1.3.1 ROC 曲线

ROC 曲线的 Receiver Operating Characteristic 曲线的简称，中文名是“受试者工作特征”，起源于军事领域，后广泛应用于医学领域。

它的横坐标是假正例率(False Positive Rate, FPR)，纵坐标是真正例率(True Positive Rate, TPR)，两者的定义分别如下：
$$\begin{gathered} TPR=\frac{TP}{TP+FN}, \\ FPR=\frac{FP}{FP+TN} \end{gathered}$$
TPR 表示正类中被分类器预测为正类的概率，刚好就等于正类的召回率；

FPR 表示负类中被分类器预测为正类的概率，它等于 1 减去负类的召回率，负类的召回率如下，称为真反例率(True Negative Rate, TNR), 也被称为特异性，表示负类被正确分类的比例。
$$TNR=\frac{TN}{FP+TN}$$

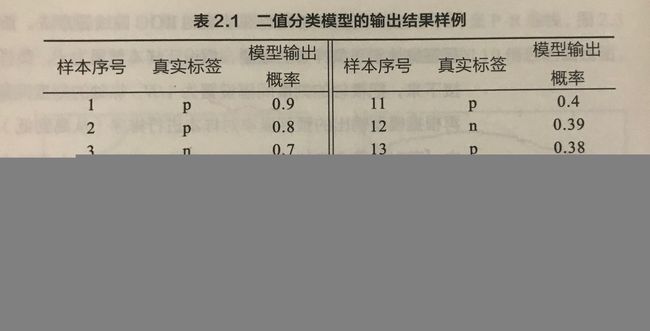
跟 P-R 曲线的绘制一样，ROC 曲线其实也是通过不断调整区分正负类结果的阈值来绘制得到的，它的纵轴是 TPR，横轴是 FPR，这里借鉴《百面机器学习》上的示例来介绍，首先有下图所示的表格，表格是一个二分类模型的输出结果样例，包含 20 个样本，然后有对应的真实标签，其中 p 表示是正类别，而 n 表示是负类别。然后模型输出概率表示模型对判断该样本是正类的置信度。

最开始如果设置阈值是无穷大的时候，那么模型会将所有样本判断为负类，TP 和 FP 都会是 0，也就是 TPR 和 FPR 必然也是 0，ROC 曲线的第一个坐标就是 (0, 0)。接着，阈值设置为 0.9，此时样本序号为 1 的样本会被判断为正样本，并且它确实是正样本，那么 TP = 1，而正类样本的个数是有 10 个，所有 TPR = 0.1；然后没有预测错误的正类，即 FP = 0，FPR = 0，这个时候曲线的第二个坐标就是 (0, 0.1)。

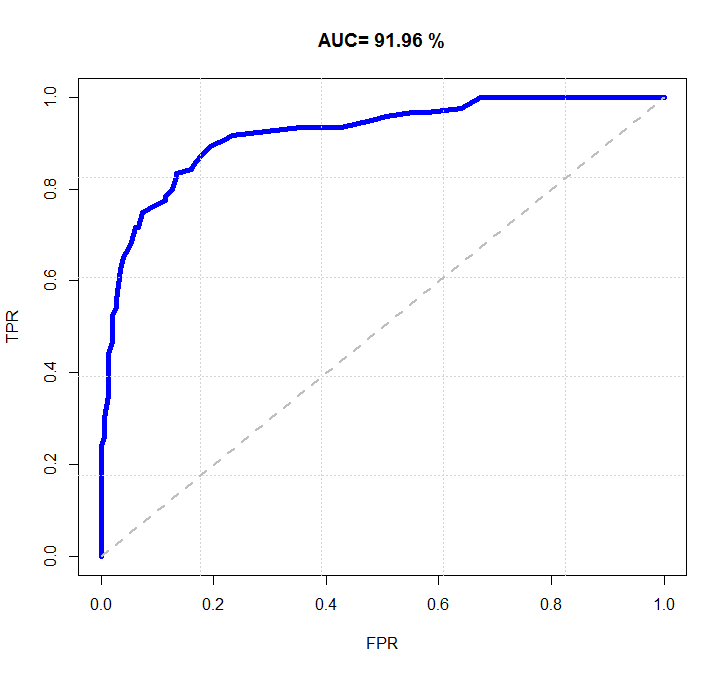
通过不断调整阈值，就可以得到曲线的不同坐标，最终得到下图所示的 ROC 曲线。

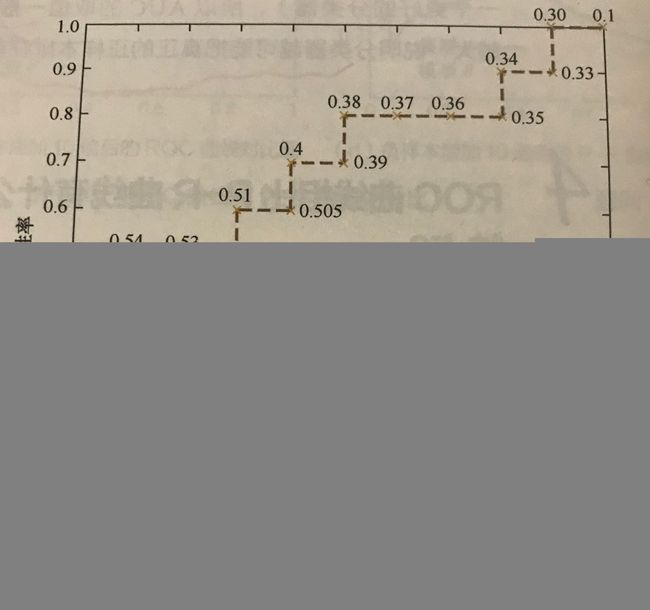
第二种更直观地绘制 ROC 曲线的方法，首先统计出正负样本的数量，假设分别是 P 和 N，接着，将横轴的刻度间隔设置为 1/N，纵轴的刻度间隔设置为 1/P。然后根据模型输出的概率对样本排序，并按顺序遍历样本，从零点开始绘制 ROC 曲线，每次遇到一个正样本就沿纵轴方向绘制一个刻度间隔的曲线，遇到一个负样本就沿横轴绘制一个刻度间隔的曲线，直到遍历完所有样本，曲线最终停留在 (1,1) 这个点，此时就完成了 ROC 曲线的绘制了。

当然，更一般的 ROC 曲线是如下图所示的，会更加的平滑，上图是由于样本数量有限才导致的。

对于 ROC 曲线，有以下几点特性：

1.ROC 曲线通常都是从左下角 (0,0) 开始，到右上角 (1,1) 结束。

• 开始时候，第一个样本被预测为正类，其他都是预测为负类别；
  • TPR 会很低，几乎是 0，上述例子就是 0.1，此时大量正类没有被分类器找出来；
  • FPR 也很低，可能就是0，上述例子就是 0，这时候被预测为正类的样本可能实际也是正类，所以几乎没有预测错误的正类样本。
• 结束时候，所有样本都预测为正类。
  • TPR 几乎就是 1，因为所有样本都预测为正类，那肯定就找出所有的正类样本了；
  • FPR 也是几乎为 1，因为所有负样本都被错误判断为正类。

2.ROC 曲线中：

• 对角线对应于随机猜想模型，即概率为 0.5；
• 点 (0,1) 是理想模型，因为此时 TPR=1，FPR=0，也就是正类都预测出来，并且没有预测错误；
• 通常，ROC 曲线越接近点 (0, 1) 越好。

3.同样可以根据 ROC 曲线来判断两个分类器的性能：

• 如果分类器 A 的 ROC 曲线被分类器 B 的曲线完全包住，可以说 B 的性能好过 A，这对应于上一条说的 ROC 曲线越接近点 (0, 1) 越好；
• 如果两个分类器的 ROC 曲线发生了交叉，则同样很难直接判断两者的性能优劣，需要借助 ROC 曲线下面积大小来做判断，而这个面积被称为 AUC:Area Under ROC Curve。

简单的代码实现如下：

def true_negative_rate(y_true, y_pred):
    true_negative = sum(1 - (yi or yi_hat) for yi, yi_hat in zip(y_true, y_pred))
    actual_negative = len(y_true) - sum(y_true)
    return true_negative / actual_negative


def roc(y, y_hat_prob):
    thresholds = sorted(set(y_hat_prob), reverse=True)
    ret = [[0, 0]]
    for threshold in thresholds:
        y_hat = [int(yi_hat_prob >= threshold) for yi_hat_prob in y_hat_prob]
        ret.append([recall(y, y_hat), 1 - true_negative_rate(y, y_hat)])
    return ret

简单的测试例子如下：

y_true = [1, 0, 1, 0, 1]
y_hat_prob = [0.9, 0.85, 0.8, 0.7, 0.6]

roc_list = roc(y_true, y_hat_prob)
print('roc_list:', roc_list)
# 输出结果是 roc_list: [[0, 0], [0.3333333333333333, 0.0], [0.3333333333333333, 0.5], [0.6666666666666666, 0.5], [0.6666666666666666, 1.0], [1.0, 1.0]]

1.3.2 ROC 和 P-R 曲线的对比

相同点

1.两者刻画的都是阈值的选择对分类度量指标的影响。虽然每个分类器对每个样本都会输出一个概率，也就是置信度，但通常我们都会人为设置一个阈值来影响分类器最终判断的结果，比如设置一个很高的阈值–0.95，或者比较低的阈值–0.3。

• 如果是偏向于精确率，则提高阈值，保证只把有把握的样本判断为正类，此时可以设置阈值为 0.9，或者更高；
• 如果偏向于召回率，那么降低阈值，保证将更多的样本判断为正类，更容易找出所有真正的正样本，此时设置阈值是 0.5，或者更低。

2.两个曲线的每个点都是对应某个阈值的选择，该点是在该阈值下的 (精确率，召回率) / (TPR, FPR)。然后沿着横轴方向对应阈值的下降。

不同

相比较 P-R 曲线，ROC 曲线有一个特点，就是正负样本的分布发生变化时，它的曲线形状能够基本保持不变。如下图所示:

分别比较了增加十倍的负样本后， P-R 和 ROC 曲线的变化，可以看到 ROC 曲线的形状基本不变，但 P-R 曲线发生了明显的变化。

所以 ROC 曲线的这个特点可以降低不同测试集带来的干扰，更加客观地评估模型本身的性能，因此它适用的场景更多，比如排序、推荐、广告等领域。

这也是由于现实场景中很多问题都会存在正负样本数量不平衡的情况，比如计算广告领域经常涉及转化率模型，正样本的数量往往是负样本数量的千分之一甚至万分之一，这时候选择 ROC 曲线更加考验反映模型本身的好坏。

当然，如果希望看到模型在特定数据集上的表现，P-R 曲线会更直观地反映其性能。所以还是需要具体问题具体分析。

1.3.3 AUC 曲线

AUC 是 ROC 曲线的面积，其物理意义是：从所有正样本中随机挑选一个样本，模型将其预测为正样本的概率是 $p_1$；从所有负样本中随机挑选一个样本，模型将其预测为正样本的概率是 $p_0$。$p_1>p_0$ 的概率就是 AUC。

AUC 曲线有以下几个特点：

• 如果完全随机地对样本进行分类，那么 $p_1>p_0$ 的概率是 0.5，则 AUC=0.5；

• AUC 在样本不平衡的条件下依然适用。

  如：在反欺诈场景下，假设正常用户为正类（设占比 99.9%），欺诈用户为负类（设占比 0.1%）。

  如果使用准确率评估，则将所有用户预测为正类即可获得 99.9%的准确率。很明显这并不是一个很好的预测结果，因为欺诈用户全部未能找出。

  如果使用 AUC 评估，则此时 FPR=1,TPR=1，对应的 AUC=0.5 。因此 AUC 成功的指出了这并不是一个很好的预测结果。

• AUC 反应的是模型对于样本的排序能力（根据样本预测为正类的概率来排序）。如：AUC=0.8 表示：给定一个正样本和一个负样本，在 80% 的情况下，模型对正样本预测为正类的概率大于对负样本预测为正类的概率。

• AUC 对于均匀采样不敏感。如：上述反欺诈场景中，假设对正常用户进行均匀的降采样。任意给定一个负样本 n，设模型对其预测为正类的概率为 Pn 。降采样前后，由于是均匀采样，因此预测为正类的概率大于 Pn 和小于 Pn 的真正样本的比例没有发生变化。因此 AUC 保持不变。

  但是如果是非均匀的降采样，则预测为正类的概率大于 Pn 和小于 Pn 的真正样本的比例会发生变化，这也会导致 AUC 发生变化。

• 正负样本之间的预测为正类概率之间的差距越大，则 AUC 越高。因为这表明正负样本之间排序的把握越大，区分度越高。

  如：在电商场景中，点击率模型的 AUC 要低于购买转化模型的 AUC 。因为点击行为的成本低于购买行为的成本，所以点击率模型中正负样本的差别要小于购买转化模型中正负样本的差别。

AUC 的计算可以通过对 ROC 曲线下各部分的面积求和而得。假设 ROC 曲线是由坐标为下列这些点按顺序连接而成的：
$$(x_1,y_1),(x_2,y_2),\cdots ,(x_m,y_m),其中x_1=0,x_m=1$$
那么 AUC 可以这样估算：
$$AUC=\frac{1}{2}\sum _{i=1}^{m-1}(x_{i+1}-x_i)\times (y_i+y_{i+1})$$

代码实现如下：

def get_auc(y, y_hat_prob):
    roc_val = iter(roc(y, y_hat_prob))
    tpr_pre, fpr_pre = next(roc_val)
    auc = 0
    for tpr, fpr in roc_val:
        auc += (tpr + tpr_pre) * (fpr - fpr_pre) / 2
        tpr_pre = tpr
        fpr_pre = fpr
    return auc

简单的测试样例如下：

y_true = [1, 0, 1, 0, 1]
y_hat_prob = [0.9, 0.85, 0.8, 0.7, 0.6]

auc_val = get_auc(y_true, y_hat_prob)
print('auc_val:', auc_val) # 输出是 0.5

1.4 代价矩阵

前面介绍的性能指标都有一个隐式的前提，错误都是均等代价。但实际应用过程中，不同类型的错误所造成的后果是不同的。比如将健康人判断为患者，与患者被判断为健康人，代价肯定是不一样的，前者可能就是需要再次进行检查，而后者可能错过治疗的最佳时机。

因此，为了衡量不同类型所造成的不同损失，可以为错误赋予非均等代价(unequal cost)。

对于一个二类分类问题，可以设定一个代价矩阵(cost matrix)，其中 $cos{t}_{ij}$ 表示将第 i 类样本预测为第 j 类样本的代价，而预测正确的代价是 0 。如下表所示：

	预测：第 0 类	预测：第 1 类
真实：第 0 类	0	$cos{t}_{01}$
真实： 第 1 类	$cos{t}_{10}$	0

1. 在非均等代价下，希望找到的不再是简单地最小化错误率的模型，而是希望找到最小化总体代价 total cost 的模型。

2. 在非均等代价下，ROC 曲线不能直接反映出分类器的期望总体代价，此时需要使用代价曲线 cost curve

   • 代价曲线的横轴是正例概率代价，如下所示，其中 p 是正例(第 0 类)的概率

   $$P_{+cost}=\frac{p\times cos{t}_{01}}{p\times cos{t}_{01}+(1-p)\times cos{t}_{10}}$$

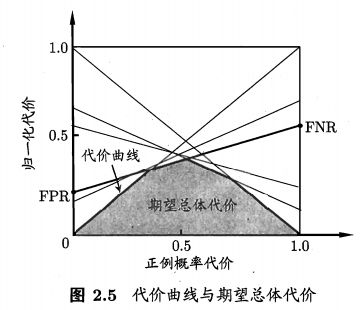
   • 代价曲线的纵轴是归一化代价，如下所示：
     $$cos{t}_{norm}=\frac{FNR\times p\times cos{t}_{01}+FPR\times (1-p)\times cos{t}_{10}}{p\times cos{t}_{01}+(1-p)\times cos{t}_{10}}$$
     其中，假正例率 FPR 表示模型将负样本预测为正类的概率，定义如下：
     $$FPR=\frac{FP}{TN+FP}$$
     假负例率 FNR 表示将正样本预测为负类的概率，定义如下：
     $$FNR=1-TPR=\frac{FN}{TP+FN}$$
     代价曲线如下图所示：

     

1.5 回归问题的性能度量

对于回归问题，常用的性能度量标准有：

1.均方误差(Mean Square Error, MSE)，定义如下：
$$MSE=\frac{1}{N}\sum _{i=1}^N(y_i-\widehat{y_i}{)}^2$$
2.均方根误差(Root Mean Squared Error, RMSE)，定义如下：
$$RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^N(y_i-\widehat{y_i}{)}^2}$$
3.均方根对数误差(Root Mean Squared Logarithmic Error, RMSLE)，定义如下
$$RMSLE=\sqrt{\frac{1}{N}\sum _{i=1}^N[log(y_i+1)-log(\widehat{y_i}+1){]}^2}$$
4.平均绝对误差(Mean Absolute Error, MAE)，定义如下：
$$MAE=\frac{1}{N}\sum _{i=1}^N|y_i-\widehat{y_i}|$$
这四个标准中，比较常用的第一个和第二个，即 MSE 和 RMSE，这两个标准一般都可以很好反映回归模型预测值和真实值的偏离程度，但如果遇到个别偏离程度非常大的离群点时，即便数量很少，也会让这两个指标变得很差。

遇到这种情况，有三种解决思路：

• 将离群点作为噪声点来处理，即数据预处理部分需要过滤掉这些噪声点；
• 从模型性能入手，提高模型的预测能力，将这些离群点产生的机制建模到模型中，但这个方法会比较困难；
• 采用其他指标，比如第三个指标 RMSLE，它关注的是预测误差的比例，即便存在离群点，也可以降低这些离群点的影响；或者是 MAPE，平均绝对百分比误差(Mean Absolute Percent Error)，定义为：

$$MAPE=\sum _{i=1}^n|\frac{y_i-\widehat{y_i}}{y_i}|\times \frac{100}{n}$$

RMSE 的简单代码实现如下所示：

def rmse(predictions, targets):
    # 真实值和预测值的误差
    differences = predictions - targets
    differences_squared = differences ** 2
    mean_of_differences_squared = differences_squared.mean()
    # 取平方根
    rmse_val = np.sqrt(mean_of_differences_squared)
    return rmse_val

1.6 其他评价指标

1. 计算速度：模型训练和预测需要的时间；
2. 鲁棒性：处理缺失值和异常值的能力；
3. 可拓展性：处理大数据集的能力；
4. 可解释性：模型预测标准的可理解性，比如决策树产生的规则就很容易理解，而神经网络被称为黑盒子的原因就是它的大量参数并不好理解。

---

小结

本文主要是基于二分类问题来介绍分类问题方面的几种性能评估，它们都是非常常用的评价指标，通常实际应用中也主要是采用这几种作为评估模型性能的方法。

---

参考：

• 《机器学习》–周志华
• 《百面机器学习》
• 《hands-on-ml-with-sklearn-and-tf》
• 9. 模型评估
• 分类模型评估的方法及Python实现

欢迎关注我的微信公众号–机器学习与计算机视觉，或者扫描下方的二维码，大家一起交流，学习和进步！

往期精彩推荐

机器学习系列

• 机器学习入门系列（1）–机器学习概览
• 机器学习入门系列(2)–如何构建一个完整的机器学习项目(一)
• 机器学习数据集的获取和测试集的构建方法
• 特征工程之数据预处理（上）
• 特征工程之数据预处理（下）
• 特征工程之特征缩放&特征编码
• 特征工程(完)
• 常用机器学习算法汇总比较(上）
• 常用机器学习算法汇总比较(中）
• 常用机器学习算法汇总比较(完）

Github项目 & 资源教程推荐

• [Github 项目推荐] 一个更好阅读和查找论文的网站
• [资源分享] TensorFlow 官方中文版教程来了
• 必读的AI和深度学习博客
• [教程]一份简单易懂的 TensorFlow 教程
• [资源]推荐一些Python书籍和教程，入门和进阶的都有！
• [Github项目推荐] 机器学习& Python 知识点速查表
• [Github项目推荐] 推荐三个助你更好利用Github的工具