【图像超分辨率】Deep Learning for Image Super-resolution: A Survey
Deep Learning for Image Super-resolution: A Survey
- 用于图像超分辨率的深度学习综述
-
- 1 介绍
- 2 问题设置和术语
-
- 2.1 问题定义
- 2.2 超分辨率数据集
- 2.3 图像质量评估
-
- 2.3.1 峰值信噪比 Peak Signal-to-Noise Ratio
- 2.3.2 结构相似度 Structural Similarity
- 2.3.3 平均意见得分 Mean opinion score
- 2.3.4 基于学习的感知质量 Learning-based Perceptual Quality
- 2.3.5 基于任务的评估 Task-based Evaluation
- 2.3.6 其它质量评估方法 Other IQA Methods
- 2.4 操作通道
- 3 有监督的超分辨率
-
- 3.1 超分辨率框架
-
- 3.1.1 预上采样超分辨率
- 3.1.2 后上采样超分辨率
- 3.1.3 渐进式升频超分辨率
- 3.1.4 迭代上下采样超分辨率
- 3.2 上采样方法
-
- 3.2.1 基于插值的升采样
- 3.2.2 基于学习的上采样
- 3.3 网络设计
-
- 3.3.1 残差学习
- 3.3.2 递归学习
- 3.3.3 多路径学习
- 3.3.4 密集连接
- 3.3.5 注意机制通道注意
- 3.3.6 高级卷积
- 3.3.7 区域递归学习
- 3.3.8 金字塔池化
- 3.3.9 小波变换
- 3.3.10 Desubpixel
- 3.3.11 xUnit
- 3.4 学习策略
-
- 3.4.1 损失函数
-
- 像素损失 Pixel Loss
- 内容损失 Content Loss
- 上下文损失 Texture Loss
- 对抗性损失 Adversarial Loss
- 循环一致性损失 Cycle Consistency Loss
- 3.4.2 批量归一化
- 3.4.3 课程学习
- 3.4.4 多重监督
- 3.5 其他改进
-
- 3.5.1上下文网络融合
- 3.5.2 数据增强
- 3.5.3 多任务学习
- 3.5.4 网络插值
- 3.5.5 自集合
- 3.6 最先进的超分辨率模型
- 4 无监督的超分辨率
-
- 4.1 零点超分辨率
- 4.2 弱监督超分辨
- 4.3 深度图像先验
- 参考文献
用于图像超分辨率的深度学习综述
1 介绍
本文总结了深度学习方法进行图像超分辨率的最新进展,将现有的SR技术研究大致分为三大类:监督SR、无监督的SR、特定领域的SR。此外,还介绍了公开的基准数据集和性能评估指标,最后强调了几个未来的方向和今后应进一步解决的问题。

2 问题设置和术语
2.1 问题定义
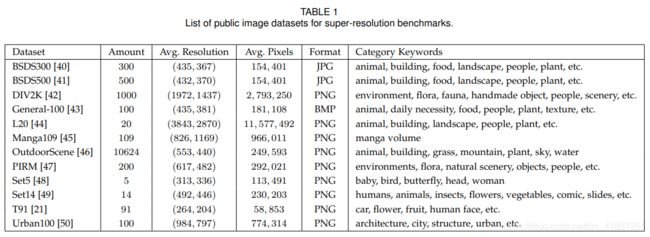
2.2 超分辨率数据集
2.3 图像质量评估
2.3.1 峰值信噪比 Peak Signal-to-Noise Ratio
由于PSNR只与像素级MSE有关,只关心对应像素之间的差异,而我们通常更关注人类的感知,所以往往导致在真实场景中重建质量的性能不佳。但由于必须与文献作品进行比较,且缺乏完全准确的感知指标,PSNR仍然是目前SR模型最广泛使用的评价标准。
2.3.2 结构相似度 Structural Similarity
考虑到人类视觉系统(HVS)高度适应于提取图像结构[59],基于亮度、对比度和结构的独立比较,提出了结构相似度指数(SSIM)[58],用于测量图像之间的结构相似度。由于SSIM是从HVS的角度来评价重建质量的,所以比较符合感知评估的要求[60],[61],也得到了广泛的应用。
2.3.3 平均意见得分 Mean opinion score
平均意见得分(MOS)测试是一种常用的主观IQA法,即要求人类测评员进行将感知质量分数分配给测试图像。通常情况下。分数从1(坏)到5(好)。而最后的MOS 是以所有评分的算术平均值计算的。虽然MOS测试是一种符合实际的IQA方法,它有一些固有的缺陷,如非线性感知的评分标准的尺度、偏差和差异。感性质量,在这种情况下,MOS测试是最重要的。最可靠的IQA方法,以准确测量感性质量[8]、[25]、[46]、[62]、[63]、[64]、[65]。
2.3.4 基于学习的感知质量 Learning-based Perceptual Quality
为了更好地评估图像的感知质量,同时减少人工干预,研究人员尝试评估通过在大型数据集上学习,提高感知质量。具体来说,Ma等人[66]和Talebi等人[67]提出了无参照物 Ma和NIMA,分别是从视觉中学习到的,并直接预测质量分数,而没有真实的参考图像。与此相反,Kim等[68]提出了DeepQA,它通过预测图像的视觉相似度,训练三联变形图像,客观误差图和主观评分。而Zhang等[69]收集了一个大尺度的感知相似性数据集,评估了感知的 图像补丁相似度(LPIPS)的差异,根据图像中的 深度特征,通过训练的深度网络,并显示出了 由CNN学习的深度特征,建立感知相似性模型。
2.3.5 基于任务的评估 Task-based Evaluation
根据SR模型往往可以帮助其他视觉任务[6],[7],[8],[9]的事实,通过其他任务来评估重建性能是另一种有效的方法。具体来说,研究人员将原始图像和重建后的HR图像输入到训练好的模型中,通过比较对预测性能的影响来评估重建质量。用于评估的视觉任务包括物体识别[8]、[70]、人脸识别[71]、[72]、人脸对齐和解析[30]、[73]等。
2.3.6 其它质量评估方法 Other IQA Methods
除上述IQA方法外,还有其他一些不太常用但流行的 SR 指标。多尺度结构相似性(MS-SSIM)[74]比单尺度SSIM更灵活。特征相似度(FSIM)[75]基于相位一致性和图像梯度幅度提取人类感兴趣的特征点来评估图像质量。自然图像质量评估器(NIQE)[76]利用在自然图像中观察到的统计规律性的可测量偏差,而不暴露在失真图像中。最近,Blau等人[77]用数学方法证明了失真度(如PSNR、SSIM)和感知质量(如MOS)是相互矛盾的,并表明随着失真度的降低,感知质量一定更差。因此如何准确测量SR质量仍是一个亟待解决的问题。
2.4 操作通道
除了常用的RGB色彩空间外, YCbCr色彩空间也被广泛用于SR。
在这个空间中,图像由Y、Cb、Cr通道表示,分别表示亮度、蓝差和红差色度成分。
早期的模型倾向于在YCbCr空间的Y通道上操作[26]、[43]、[78]、[79],而最近的模型则倾向于在RGB通道上操作[28]、[31]、[57]、[70]。
在不同的色彩空间或通道上进行操作(训练或评估),会使评估结果相差很大[23]。
3 有监督的超分辨率
现有的基于深度学习的超分辨率模型主要是有监督的SR,即用LR图像和相应的HR图像进行训练。虽然这些模型之间的差异非常大,但它们本质上是模型框架、上采样方法、网络设计和学习策略等一系列组件的组合。从这个角度来看,研究人员将这些组件组合起来,建立一个综合的SR模型,以适应特定的目的。
3.1 超分辨率框架
由于图像超分辨率是一个不确定的问题,如何进行上采样(即从LR输入生成HR输出)是关键问题。虽然现有模型的架构差异很大,但根据所采用的上采样操作及其在模型中的位置,可以归纳为四种模型框架(如图2所示)。


图2:基于深度学习的超分辨率模型框架。立方体大小代表输出大小。灰色的表示预定义的上采样,绿色、黄色和蓝色的分别表示可学习的上采样、下采样和卷积层。而虚线框围起来的块代表可堆叠的模块。
3.1.1 预上采样超分辨率
由于直接学习从低维空间到高维空间的映射存在困难,相应的解决方案是,利用传统的上采样算法获得更高分辨率的图像,然后利用深度神经网络进行细化。因此Dong等[22]、[23]首先采用预上采样SR框架(如图2a所示),提出SRCNN从插值的LR图像到HR图像学习端到端的映射。具体来说,利用传统方法(如双立方插值)将LR图像上采样成所需尺寸的粗HR图像,然后在这些图像上应用深度CNNs重建高质量细节。由于已经完成了最困难的上采样操作,CNNs只需要对粗图像进行细化,从而大大降低了学习难度。此外,这些模型可以将任意尺寸和缩放因子的插值图像作为输入,并给出与单尺度SR模型性能相当的精细化结果[26]。因此它逐渐成为最流行的框架之一[55],[56],[82],[83],这些模型的主要区别在于后置模型设计(3.3节)和学习策略(3.4节)。但是,预定义的上采样往往会引入副作用(如噪声放大和模糊),而且由于大多数操作都是在高维空间中进行的,因此时间和空间成本比其他框架[43],[84]要高得多。
3.1.2 后上采样超分辨率
为了提高计算效率,充分利用深度学习技术自动提高分辨率,研究者提出在低维空间中进行大部分计算,用集成在模型末端的端到端可学习层代替预定义的上采样。在这一框架[43]、[84]中,即后上采样SR如图2b所示,LR输入图像在不提高分辨率的情况下被送入深度CNN,并在网络末端应用端到端可学习的上采样层。由于计算成本巨大的特征提取过程只发生在低维空间,且分辨率只在末端增加,计算和空间复杂度大大降低。因此,该框架也成为最主流的框架之一[25],[31],[79],[85]。这些模型主要在可学习的上采样层(Sec.3.2)、前CNN结构(Sec.3.3)和学习策略(Sec.3.4)等方面存在差异。
3.1.3 渐进式升频超分辨率
虽然后上采样SR框架极大地降低了计算成本,但仍存在一些不足。一方面,上采样只进行了一步,这大大增加了大缩放因子(如4,8)的学习难度。另一方面,每个缩放因子都需要训练一个独立的SR模型,无法应对多尺度SR的需求。为了解决这些缺点,如图2c所示,拉普拉斯金字塔SR网络(LapSRN)[27]采用了渐进式上采样框架。具体来说,该框架下的模型基于CNN的级联,逐步重建更高分辨率的图像。在每一个阶段,图像都会被上采样到更高的分辨率,并由CNNs进行完善。其他工作如MS-LapSRN[65]和渐进式SR(ProSR)[32]也采用了这一框架,并实现了比较高的性能。与LapSRN和MS-LapSRN将中间重建的图像作为后续模块的 "基础图像 "不同,ProSR保留了主信息流,并由各个头重建中间分辨率的图像。通过将一个困难的任务分解为简单的任务,该框架下的模型大大降低了学习难度,尤其是在大因子的情况下,还可以应对多尺度的SR,而不会引入过多的空间和时间成本。此外,一些特定的学习策略,如课程式学习(3.4.3节)和多监督(3.4.4节)可以直接整合,进一步降低学习难度,提高最终的成绩。但这些模型也遇到了一些问题,如多阶段的模型设计复杂,训练稳定性差等,需要更多的建模指导和更先进的训练策略。
3.1.4 迭代上下采样超分辨率
为了更好地捕捉LR和HR图像对的相互依赖性,在SR[44]中加入了一种高效的迭代程序,名为反向传播(back-projection)[12]。这个SR框架,即迭代上下采样SR(如图2d所示),尝试迭代应用反向传播细化,即计算重建误差后再融合回调HR图像强度。具体来说,Haris等[57]利用迭代的上下采样层,提出了DBPN,将上采样层和下采样层交替连接起来,利用中间所有的重建结果重建最终的HR结果。同样,SRFBN[86]采用了迭代的上下采样反馈块,跳过连接更密集,学习到了更好的表示方法。而用于视频超分辨率的RBPN[87]从连续视频帧中提取上下文,并将这些上下文结合起来,通过反向传播模块产生循环输出帧。
该框架下的模型可以更好地挖掘LR-HR图像对之间的深层关系,从而提供更高质量的重建结果。尽管如此,反向传播模块的设计标准仍不明确。由于该机制刚刚被引入到基于深度学习的SR中,该框架具有很大的潜力,需要进一步探索。
3.2 上采样方法
除了模型中的升频位置,如何进行上采样也非常重要。虽然已经有各种传统的上采样方法[20]、[21]、[88]、[89],但利用CNNs学习端到端上采样已经逐渐成为一种趋势。在本节中,我们将介绍一些传统的基于插值的算法和基于深度学习的上采样层。
3.2.1 基于插值的升采样
图像插值,又称图像缩放,是指调整数字图像的大小,被图像相关应用广泛使用。传统的插值方法包括最近邻插值、双线性和双立方插值、Sinc和Lanczos重采样等。由于这些方法可解释性强,易于实现,因此其中一些方法仍被广泛用于基于CNN的SR模型中。
-
最近邻插值法(Nearest-neighbor Interpolation)。最近邻插值是一种简单直观的算法。它为每个位置选择最近的像素的值进行插值,而不考虑任何其他像素。因此这种方法速度非常快,但通常产生的结果块状,质量不高。
-
双线插值法(Bilinear Interpolation)双线插值(BLI)首先在图像的一个轴上进行线性插值,然后在另一个轴上执行,如图3所示。由于它的结果是二次插值,接受场大小为2×2,所以在保持相对较快速度的同时,表现出比最近邻插值更好的性能。
-
双立方插值(Bicubic Interpolation)同样,双立方插值(BCI)[10]在两个轴上分别进行立方插值,如图3所示。与BLI相比,BCI考虑了4×4个像素,结果更平滑,伪影更少,但速度更低。事实上,带抗锯齿的BCI是构建SR数据集(即将HR图像降级为LR图像)的主流方法,也被广泛应用于预上采样SR框架中(参见3.1.1)。事实上,基于插值的上采样方法只是基于自身的图像信号提高了图像分辨率,而没有带来更多的信息。相反,它们往往会带来一些副作用,如计算复杂度、噪声放大、模糊结果等。
因此,目前的趋势是用可学习的上采样层取代基于插值的方法。
3.2.2 基于学习的上采样
为了克服基于插值方法的缺点,以端到端的方式学习上采样,在SR领域引入了转置卷积层和亚像素层。
-
转置卷积层又称解卷积层[90]、[91],试图与正常卷积相反地进行变换,即根据大小像卷积输出的特征图来预测可能的输入。具体来说,它通过插入零点扩大图像并进行卷积来提高图像分辨率。以2×SR与3×3内核为例(如图4所示),首先将输入扩大到原来大小的两倍,其中增加的像素值设为0(图4b)。然后应用核大小为3×3、跨度为1、填充为1的卷积(图4c)。在这种情况下,输入被上采样了2个因子,在这种情况下,接受场最多是2×2。由于转置卷积以端到端的方式扩大了图像大小,同时保持了与香草卷积兼容的连接模式,因此它被广泛地用作SR模型中的上采样层[57]、[78]、[79]、[85]。但是,该层很容易造成每个轴上的 “不均匀重叠”[92],两个轴上的乘法结果会进一步形成大小不一的棋盘式模式,从而伤害SR性能。
子像素层。

-
子像素层[84]是另一个端到端可学习的上采样层,通过卷积生成多个通道,然后对它们进行重塑,进行上采样,如图5所示。在该层中,首先应用卷积来产生s2倍通道的输出,其中s是缩放因子(图5b)。假设输入大小为h×w×c,则输出大小为h×w×s2c。之后,执行重塑操作(也就是shuffle[84]),产生大小为sh × sw ×c的输出(图5c)。在这种情况下,接受场可以达到3×3。由于端到端的上采样方式,该层也被SR模型广泛使用[25]、[28]、[39]、[93]。与转置卷积层相比,子像素层具有更大的接受场,可以提供更多的上下文信息,帮助生成更真实的细节。然而,由于接受场的分布是不均匀的,块状区域实际上共享相同的接受场,因此可能会导致不同块状区域的边界附近出现一些伪影。另一方面,独立预测块状区域中的相邻像素可能会导致不平滑的输出。因此Gao等人[94]提出了PixelTCL,将独立预测替换为相互依赖的顺序预测,并产生更平滑、更一致的结果。

-
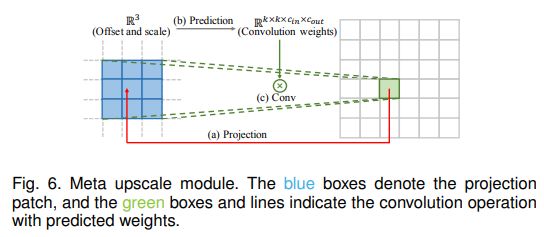
元上标模块前面的方法需要预先定义缩放因子,即针对不同的因子训练不同的上采样模块,效率低下,不符合实际需求。因此,Hu等[95]提出了元上采样模块(如图6所示),首先基于元学习解决任意缩放因子的SR。具体来说,对于HR图像上的每个目标位置,该模块将其投影到LR特征图上的一个小斑块上(即k×k×Cin),根据投影偏移量和缩放因子按密层预测卷积权重(即k×k×Cin×Cout),并进行卷积。这样一来,元上标模块可以通过一个模型对其进行任意系数的不断放大。而且由于训练数据量大(多个因子同时训练),该模块可以在固定因子上表现出相当甚至更好的性能。虽然该模块在推理过程中需要预测权重,上采样模块的执行时间只占特征提取时间的1%左右[95]。但这种方法根据与图像内容无关的几个值,为每个目标像素预测大量的卷积权值,因此在面对较大的放大倍数时,预测结果可能不稳定,效率较低。目前,这些基于学习的图层已经成为最广泛使用的上采样方法。特别是在后上采样框架中(Sec.3.1.2),这些图层通常被用于最后的上采样阶段,用于基于低维空间中提取的高级表征重建HR图像,从而实现端到端的SR,同时避免高维空间中的过度操作。
3.3 网络设计
现在网络设计已经是深度学习中最重要的部分之一。在超分辨率领域,研究者在四个SR框架(Sec.3.1)的基础上,应用各种网络设计策略来构建最终的网络。在本节中将这些网络分解为网络设计的基本原则和策略,逐一介绍并分析其优势和局限性。
3.3.1 残差学习
在He等人[96]提出ResNet用于学习残差而不是彻底的映射之前,残差学习已经被SR模型[48]、[88]、[97]广泛采用,如图7a所示。其中,残差学习策略大致可以分为全局残差学习和局部残差学习。

全局残差学习由于图像SR是一个图像到图像的转移任务,输入图像与目标图像高度相关,因此研究者尝试只学习它们之间的残差,即全局残差学习。在这种情况下,它避免了学习一个完整图像到另一个图像的复杂变换,而只需要学习一个残差图来还原缺失的高频细节。由于大多数区域的残差接近于零,模型的复杂度和学习难度大大降低。因此被SR模型广泛使用[26],[55],[56],[98]。
局部残差学习局部残差学习类似于ResNet[96]中的残差学习,用于缓解网络深度不断增加带来的退化问题[96],降低训练难度,提高学习能力。它也被广泛应用于SR[70]、[78]、[85]、[99]。在实际应用中,上述方法都是通过快捷连接(通常用一个小常数来缩放)和元素加法来实现的,而不同的是,前者直接连接输入和输出图像,而后者通常在网络内部不同深度的层之间增加多个快捷连接(shortcuts)。
3.3.2 递归学习
为了在不引入过多参数的情况下学习更高层次的特征,SR领域引入了递归学习,即以递归的方式多次应用同一模块,如图7b所示。其中,16次递归的DRCN[82]采用单卷积层作为递归单元,在没有过多参数的情况下,达到了41×41的接受场,比SRCNN[22]的13×13大得多。DRRN[56]采用ResBlock[96]作为25次递归的递归单元,获得的性能甚至比17-ResBlock基线更好。后来Tai等[55]提出了基于记忆块的MemNet,它是由一个6-递归的ResBlock组成的,每个递归的输出都会被连在一起,并经过额外的1×1卷积进行记忆和遗忘。级联残差网络(cascading residual network,CARN)[28]也采用了类似的递归单元,包括多个ResBlocks。最近,Li等[86]采用迭代上下采样SR框架,提出了一种基于递归学习的反馈网络,整个网络的权重在所有递归中共享。此外,研究者还在不同部分采用了不同的递归模块。具体来说,Han等人[85]提出了双状态递归网络(Dual-state recurrent network,DSRN)来交换LR和HR状态之间的信号。在每个时间步长(即递归),每个分支的表示都会被更新和交换,以更好地探索LR-HR关系。同样,Lai等人[65]采用嵌入和上采样模块作为递归单元,因此以很少的性能损失为代价,大大减小了模型大小。一般来说,递归学习确实可以在不引入过多参数的情况下学习更高级的表示,但仍然无法避免高额的计算成本。而且它内在地带来了消失或爆炸梯度问题,因此一些技术如残差学习(3.3.1节)和多重监督(3.4.4节)常常与递归学习相结合,以缓解这些问题[55],[56],[82],[85]。
3.3.3 多路径学习
多路径学习是指将特征通过多条路径,进行不同的操作,并将其融合回来,以提供更好的建模能力。具体来说,可以分为全局、局部和特定尺度的多路径学习,具体如下。
全局多路径学习
全局多路径学习是指利用多条路径来提取图像不同方面的特征。这些路径在传播过程中可以相互交叉,从而大大提高了学习能力。具体来说,LapSRN[27]包括一条从粗到细的预测子带残差的特征提取路径和另一条基于两条路径信号重建HR图像的路径。同样,DSRN[85]利用两条路径分别在低维和高维空间中提取信息,并不断交换信息,进一步提高学习能力。而像素递归超解[64]采用条件路径来捕捉图像的全局结构,采用先验路径来捕捉生成像素的序列依赖性。而Ren等[100]则采用非平衡结构的多路径进行上采样,并在模型最后进行融合。
局部多路径学习
受inception模块[101]的启发,MSRN[99]采用了一个新的块来进行多尺度特征提取,如图7e所示。在这个块中,采用了两个核大小为3 ⇥ 3和5 ⇥ 5的卷积层来同时提取特征,然后将输出结果连在一起,再经过同样的操作,最后应用额外的1 ⇥ 1卷积。通过元素相加的捷径将输入和输出连接起来。通过这样的局部多路径学习,SR模型可以更好地提取多尺度的图像特征,进一步提高性能。
特定尺度的多路径学习
考虑到不同尺度的SR模型需要经过类似的特征提取,Lim等人[31]提出了尺度特异性多路径学习,以单网络应对多尺度SR。具体来说,他们共享了模型的主成分(即特征提取的中间层),并在网络的开始和结束处分别附加了特定尺度的预处理路径和上采样路径(如图7f所示)。在训练过程中,只启用和更新所选尺度对应的路径。这样,所提出的MDSR[31]通过共享不同尺度的大部分参数,大大减小了模型的大小,并表现出与单尺度模型相当的性能。CARN[28]和ProSR[32]也采用了类似的特定尺度多路径学习。
3.3.4 密集连接
自Huang等[102]提出基于密集块的DenseNet以来,密集连接在视觉任务中越来越受欢迎。对于密集块中的每一层,将前面所有层的特征图作为输入,并将自己的特征图作为输入进入所有后续层。密集连接不仅有助于缓解梯度消失,增强信号传播,鼓励特征重用,而且通过采用小的增长率(即密集块中的通道数),并在连通所有输入特征图后挤压通道,大幅减小模型大小。为了融合低级和高级特征,为重建高质量的细节提供更丰富的信息,在SR领域引入了密集连接,如图7d所示。Tong等[79]不仅采用致密块构建了69层SRDenseNet,而且在不同致密块之间插入致密连接,对于每一个密集块,所有前面的块的特征图都被用作输入,其自身的特征图被用作所有后续块的输入。这些层级和块级的密集连接也被MemNet[55]、CARN[28]、RDN[93]和ESRGAN[103]所采用。DBPN[57]也广泛采用了密集连接,但他们的密集连接是在所有上采样单元之间,下采样单元也是如此。
3.3.5 注意机制通道注意
考虑到不同通道之间特征表征的相互依赖和相互作用,Hu等[104]提出了一个 "挤压-激发 "块,通过明确模拟通道相互依赖性来提高学习能力,如图7c所示。在这个块中,每个输入通道都被利用全局平均池(GAP)挤压成一个通道描述符(即常量),然后这些描述符被送入两个致密层,以产生输入通道的通道侧缩放因子。最近,Zhang等[70]将信道关注机制与SR结合,提出RCAN,明显提高了模型的表示能力和SR性能。为了更好地学习特征相关性,Dai等[105]进一步提出了二阶信道注意力(SOCA)模块。SOCA通过使用二阶特征统计来代替GAP,自适应地重新调整信道方面的特征,并能提取出更多的信息量和判别力的表示。非局部注意力。
大多数现有的SR模型具有非常有限的局部接受场。然而,一些远处的物体或纹理可能对局部补丁的生成非常重要。以至于Zhang等人[106]提出了局部和非局部注意力块,以提取捕捉像素之间长距离依赖关系的特征。具体来说,他们提出了一个用于提取特征的主干分支,和一个用于自适应重缩放主干分支特征的(非)局部掩模分支。其中,局部分支采用encoderdecoder结构来学习局部注意力,而非局部分支则利用嵌入的高斯函数来评估特征图中每两个位置指数之间的对偶关系来预测缩放权重。通过这种机制,所提出的方法很好地捕捉了空间注意力,进一步增强了表示能力。同样,Dai等[105]也结合了非局部注意力机制来捕捉长距离的空间上下文信息。
3.3.6 高级卷积
由于卷积运算是深度神经网络的基础,研究者们也试图改进卷积运算,以获得更好的性能或更高的效率。稀释卷积(Dilated Convolution)
众所周知,上下文信息有利于生成SR的真实细节。因此,Zhang等[107]在SR模型中用扩张卷积代替普通卷积,将接受场增加两倍以上,实现了更好的性能。
群体卷积(Group Convolution)
受轻量级CNN的最新进展[108]、[109]的激励,Hui等[98]和Ahn等[28]分别提出了IDN和CARN-M,用分组卷积代替了普通卷积。正如之前的一些工作所证明的那样,分组卷积大大减少了参数和操作的数量,而牺牲了一点性能损失[28],[98]。
深度可分离卷积 (Depthwise Separable Convolution)
自从Howard等人[110]提出深度可分离卷积以实现高效卷积后,它被扩展到各个领域。具体来说,它由一个因子化的深度卷积和一个点向卷积(即1 ×1卷积)组成,因此只需少量降低精度就可以减少大量的参数和运算[110]。而最近,Nie等人[81]采用了深度可分离卷积,大大加快了SR架构的速度。
3.3.7 区域递归学习
大多数SR模型将SR视为与像素无关的任务,因此不能正确地来源生成像素之间的相互依赖性。受PixelCNN[111]的启发,Dahl等人[64]首先提出了像素递归学习,通过采用两个网络分别捕捉全局上下文信息和序列生成依赖性,来进行逐个像素的生成。这样,所提出的方法在超分辨率的极低分辨率人脸图像(如8×8)上合成了逼真的头发和皮肤细节,并且远远超过了之前在MOS测试上的方法[64](Sec.2.3.3)。受人类注意力转移机制[112]的激励,Attention-FH[113]也采用了这一策略,采用循环策略网络来依次发现出席的补丁并进行局部增强。这样一来,它能够根据每个图像的自身特点,自适应地对其进行个性化的最优搜索路径,从而充分利用了图像的全局内依赖性。虽然这些方法在一定程度上表现出了较好的性能,但由于递归过程需要较长的传播路径,大大增加了计算成本和训练难度,尤其是对于超分辨率的HR图像。
3.3.8 金字塔池化
在空间金字塔池化层[114]的激励下,Zhao等人[115]提出了金字塔池化模块,以更好地利用全局和局部上下文信息。具体来说,对于尺寸为h×w×c的特征图,将每个特征图划分为M×M个分仓,并经过全局平均池化,得到M×M×c输出。然后进行1×1的卷积,将输出压缩到一个通道。之后,通过双线性插值将低维特征图上采样到与原始特征图相同的大小。通过使用不同的M,该模块有效地整合了全局以及局部的上下文信息。通过加入该模块,提出的EDSR-PP模型[116]比基线进一步提高了性能。
3.3.9 小波变换
众所周知,小波变换(WT)[117]、[118]是通过将图像信号分解为表示纹理细节的高频子带和包含全局拓扑信息的低频子带,是一种高效的图像表示方法。Bae等[119]首先将WT与基于深度学习的SR模型相结合,取插值LR小波的子带作为输入,预测相应HR子带的残差。应用WT和反WT分别对LR输入进行分解和重建HR输出。同样,DWSR[120]和小波-SRNet[121]也是在小波域进行SR,但结构更为复杂。与上述作品对每个子带进行独立处理不同,MWCNN[122]采用多级WT,并将并联的子带作为单个CNN的输入,以更好地捕捉它们之间的依赖关系。由于小波变换的高效表示,采用这种策略的模型往往在保持性能竞争力的前提下,大大降低了模型的大小和计算成本[119],[122]。
3.3.10 Desubpixel
为了加快推理速度,Vu等人[123]提出在低维空间中进行耗时的特征提取,并提出了desubpixel,即子像素层的洗牌操作的反演(Sec.3.2.2)。具体来说,desubpixel操作将图像在空间上进行分割,堆叠成额外的通道,从而避免信息的丢失。通过这种方式,它们在模型开始时通过desubpixel对输入图像进行下采样,在低维空间中学习表示,并在最后上采样到目标尺寸。所提出的模型在智能手机的PIRM挑战赛中取得了最好的成绩[81],推理速度非常快,性能良好。
3.3.11 xUnit
为了将空间特征处理和非线性激活结合起来,更高效地学习复杂的特征,Kligvasser等人[124]提出了用于学习空间激活函数的xUnit。具体来说,ReLU被认为是确定一个权重图来与输入进行逐元乘法,而xUnit则直接通过卷积和高斯门控学习权重图。虽然xUnit对计算量的要求较高,但由于其对性能的显著影响,它可以在与ReLU性能相匹配的情况下大大减小模型的大小。通过这种方式,作者在不降低性能的情况下,将模型大小减少了近50%。
3.4 学习策略
3.4.1 损失函数
在超分辨率领域,损失函数被用来衡量重建误差,指导模型优化。早期,研究者通常采用像素上的L2损失,但后来发现它不能很准确地衡量重建质量。因此,为了更好地测量重建误差,产生更真实、更高质量的结果,采用了多种损失函数(如内容损失[29]、对抗损失[25])。现在这些损失函数已经发挥了重要作用。在本节中,我们将仔细研究一下广泛使用的损失函数。本节中的记号沿用了2.1节,只是为了简洁起见,我们忽略了目标HR图像ˆIy和生成的HR图像Iy的下标y。
像素损失 Pixel Loss
内容损失 Content Loss
上下文损失 Texture Loss
对抗性损失 Adversarial Loss
循环一致性损失 Cycle Consistency Loss
3.4.2 批量归一化
为了加速和稳定深度CNN的训练,Sergey等[145]提出了批量归一化(BN),以减少网络的内部协变量偏移。具体来说,他们对每个小批进行归一化,并为每个通道训练两个额外的变换参数,以保持表示能力。由于BN可以校准中间特征分布并缓解消失梯度,因此可以使用更高的学习率,并且对初始化不那么小心。因此,这种技术被SR模型[25]、[39]、[55]、[56]、[122]、[146]广泛使用。然而,Lim等人[31]认为BN会丢失每个图像的尺度信息,并摆脱网络的范围灵活性。所以他们去掉了BN,并利用节省下来的内存成本(高达40%)开发了一个更大的模型,从而大幅提高了性能。其他一些模型[32]、[103]、[147]也采用了这一经验,实现了性能的提升。
3.4.3 课程学习
课程学习[148]是指从一个比较容易的任务开始,逐渐增加难度。由于超分辨率是一个非命题问题,总是会受到大尺度因子、噪声和模糊等不利条件的影响,为了降低学习难度,加入了课程训练。为了降低大缩放因子的SR的难度,Wang等[32]、Bei等[149]和Ahn等[150]分别提出了ProSR、ADRSR和渐进式CARN,它们不仅在架构上是渐进式的(Sec.3.1.3),而且在训练过程中也是渐进式的。训练从2×上采样开始,在完成训练后,逐步装入具有4×或更大缩放因子的部分,并与前面的部分混合。具体来说,ProSR通过线性合并本层的输出和前几层的上采样输出进行混合[151],ADRSR将它们连在一起,并附加另一个卷积层,而渐进式CARN则将前一个重建块替换成双分辨率的图像。此外,Park等[116]将8×SR问题划分为3个子问题(即1×到2×,2×到4×,4×到8×),并为每个问题训练独立网络。然后将其中的两个网络进行串联和微调,再与第三个网络进行。此外,他们还将困难条件下的4×SR分解为1×到2×、2×到4×和去噪或去杂的子问题。而SRFBN[86]则采用这种策略来处理不利条件下的SR,即从容易降级开始,逐渐增加降级复杂度。与普通的训练程序相比,课程学习大大降低了训练难度,缩短了总的训练时间,特别是对于大因子的训练。
3.4.4 多重监督
多重监督是指在模型中加入多重监督信号,以增强梯度传播,避免梯度的消失和爆炸。为了防止递归学习引入的梯度问题(参见3.3.2节),DRCN[82]将多监督与递归单元相结合。具体来说,他们将递归单元的每个输出都送入重建模块,生成HR图像,并结合所有的中间重建建立最终的预测。MemNet[55]和DSRN[85]也采取了类似的策略,它们也是基于递归学习的。此外,由于LapSRN[27]、[65]在渐进上采样框架下(参见3.1.3节),在传播过程中会产生不同尺度的中间结果,因此采用多监督策略是很直接的。具体来说,中间结果被迫与从地面真相HR图像下采样的中间图像相同。在实际应用中,这种多重监督技术往往是通过在损失函数中增加一些项来实现的,这样一来,监督信号得到了更有效的反向传播,从而降低了训练难度,提高了模型的训练效果。
3.5 其他改进
除了网络设计和学习策略外,还有其他技术可以进一步改进SR模型。
3.5.1上下文网络融合
上下文网络融合(Context-wise network fusion,CNF)[100]指的是融合多个SR网络预测的堆叠技术(即3.3.3节中多路径学习的一种特殊情况)。具体来说,他们分别训练各个不同架构的SR模型,将每个模型的预测结果输入到各个卷积层中,最后将输出结果相加就是最终的预测结果。在这个CNF框架下,三个轻量级SRCNNs[22]、[23]构建的最终模型达到了与最先进模型相当的性能,效率可以接受[100]。
3.5.2 数据增强
数据增强是深度学习提升性能最广泛使用的技术之一。对于图像超分辨率,一些有用的增强选项包括裁剪、翻转、缩放、旋转、颜色抖动等。[27], [31], [44], [56], [85], [98]. 此外,Bei等[149]还对RGB通道进行随机洗牌,不仅增强了数据,还缓解了因数据集颜色不平衡造成的颜色偏差。
3.5.3 多任务学习
多任务学习[152]是指通过利用相关任务的训练信号中包含的特定领域信息来提高泛化能力,如物体检测和语义分割[153]、头部姿势估计和面部属性推理[154]等。在SR领域,Wang等人[46]结合语义分割网络,用于提供语义知识和生成语义特定细节。具体来说,他们提出了空间特征变换,将语义图作为输入,并预测在中间特征图上执行的亲和变换的空间维度参数。因此,所提出的SFT-GAN可以在具有丰富语义区域的图像上生成更逼真、更有视觉美感的纹理。此外,考虑到直接超解噪声图像可能会造成噪声放大,DNSR[149]提出先分别训练一个去噪网络和一个SR网络,然后再将它们连通起来进行微调。同样,循环中的GAN(CinCGAN)[131]将循环中的去噪框架和循环中的SR模型结合起来,共同进行降噪和超解像。由于不同的任务往往关注数据的不同方面,因此将相关任务与SR模型相结合,通常可以通过提供额外的信息和知识来提高SR性能。
3.5.4 网络插值
基于PSNR的模型产生的图像更接近地面真实值,但会引入模糊问题,而基于GAN的模型带来更好的感知质量,但会引入令人不快的伪影(如无意义的噪声使图像更 “逼真”)。为了更好地平衡失真和感知,Wang等人[103]、[155]提出了一种网络插值策略。具体来说,他们通过微调训练一个基于PSNR的模型和训练一个基于GAN的模型,然后对两个网络的所有对应参数进行插值,得出中间模型。通过对插值权重的调整,而不对网络进行再训练,就能得到有意义的结果,而且伪影更小。
3.5.5 自集合
自集合,又称增强预测[44],是SR模型常用的一种推理技术。具体来说,对LR图像进行不同角度(0,90,180,270)的旋转和水平翻转,得到一组8幅图像。然后将这些图像输入SR模型,并对重建后的HR图像进行相应的逆向变换,得到输出结果。通过这些输出的平均值[31]、[32]、[44]、[70]、[78]、[93]或中位数[83]来进行最终的预测结果。通过这种方式,这些模型进一步提高了性能。
3.6 最先进的超分辨率模型
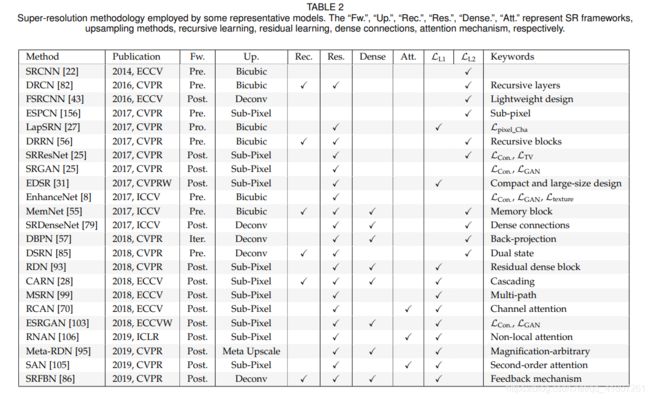
近年来,基于深度学习的图像超分辨率模型受到越来越多的关注,并取得了最先进的性能。在前面的章节中,我们将SR模型分解为具体的组成部分,包括模型框架(Sec.3.1)、上采样方法(Sec.3.2)、网络设计(Sec.3)和学习策略(Sec.3.4),对这些组成部分进行层次分析,并找出它们的优势和局限性。事实上,目前大多数最先进的SR模型基本上都可以归结为我们上面总结的多种策略的组合。例如,RCAN[70]最大的贡献来自于信道关注机制(Sec.3.5),它还采用了其他策略,如子像素上采样(Sec.3.2)、残差学习(Sec.3.1)、像素L1损失(Sec.3.4.1)和自ensemble(Sec.3.5)。
以类似的方式,我们总结了一些有代表性的模型及其关键策略,如表2所示。除了SR精度外,效率是另一个非常重要的方面,不同的策略对效率有或多或少的影响。所以在前面的章节中,我们不仅分析了所介绍策略的准确率,还指出了对效率影响较大的策略对效率的具体影响,如后上采样(Sec.3.1.2)、递归学习(Sec.3.2)、密集连接(Sec.3.4)、xUnit(Sec.3.3.11)。而且我们还对一些有代表性的SR模型进行了SR精度(即PSNR)、模型大小(即参数数量)和计算成本(即Multi-Add数量)的基准测试,如图8所示。准确度由4个基准数据集(即Set5[48]、Set14[49]、B100[40]和Urban100[50])上PSNR的平均值来衡量。而模型大小和计算成本是用PyTorch-OpCounter[157]计算的,其中输出分辨率为720p(即1080 ×720)。所有统计数据均来自于原始论文或在官方模型上计算,缩放系数为2.。
4 无监督的超分辨率
现有的超分辨率作品大多集中在监督学习上,即用匹配的LR-HR图像对进行学习。然而,由于很难收集到同一场景但具有不同分辨率的图像,SR数据集中的LR图像往往是通过对HR图像进行预定义的降级获得的。因此,训练的SR模型实际上是学习预定义降级的逆过程。为了在不引入人工降级前导的情况下学习真实世界的LR-HR映射,研究者们越来越重视无监督的SR,在这种情况下,只提供未配对的LR-HR图像进行训练,这样得到的模型更容易应对真实世界场景下的SR问题。接下来我们将简单介绍几种现有的深度学习的无监督SR模型,还有更多的方法有待探索。
4.1 零点超分辨率
考虑到单幅图像内部的图像统计量已经为SR提供了足够的信息,Shocher等[83]提出了零点超分辨率(ZSSR),通过在测试时训练特定图像的SR网络,而不是在大型外部数据集上训练一个通用模型来应对无监督的SR。具体来说,他们利用[158]从单幅图像中估计出降级内核,并利用这个内核对这个图像进行不同缩放因子的降级和增强,建立一个小数据集。然后在这个数据集上训练一个小型的SR的CNN,并用于最终的预测。这样一来,ZSSR利用了每幅图像内部的跨尺度内部递归,因此在非理想条件下(即通过非双三次插值得到的图像,受到模糊、噪声、压缩伪影等影响)的图像上,ZSSR以较大的优势(估计内核为1 dB,已知内核为2 dB)优于之前的方法,更接近真实世界的场景,而在理想条件下(即通过双ubic降级得到的图像)则给出了具有竞争力的结果。但是,由于在测试过程中需要针对不同的图像训练不同的网络,所以推理时间比其他网络要长很多。
4.2 弱监督超分辨
为了应对超分辨而不引入预定义的退化,研究者们尝试用弱监督学习来学习SR模型,即使用未配对的LRHR图像。其中,有的研究者首先学习HR到LR的退化,并用它来构建训练SR模型的数据集,有的研究者则设计周期中的网络来同时学习LR到HR和HR到LR的映射。接下来我们将详细介绍这些模型。学习的退化。由于预定义的退化是次优的,所以从未配对的LRHR数据集学习退化是一个可行的方向。Bulat等人[159]提出了一个两阶段的过程,首先使用未配对的LR-HR图像训练一个HR-to-LR GAN来学习退化,然后使用配对的LR-HR图像在第一个GAN的基础上进行SR的LR-to-HR GAN训练。具体来说,对于HR-to-LR GAN,HR图像被输入到生成器中以产生LR输出,要求其不仅与HR图像的降维(通过平均池化)获得的LR图像相匹配,而且与真实LR图像的分布相匹配。完成训练后,将生成器作为降维模型,生成LR-HR图像对。然后对于LR-to-HR的GAN,生成器(即SR模型)将生成的LR图像作为输入,并预测HR输出,要求不仅要符合相应的HR图像,还要符合HR图像的分布。通过应用这两个阶段的过程,所提出的无监督模型有效地提高了超解真实世界LR图像的质量,并比以往最先进的作品获得了较大的改进。周期中的超级解析。另一种无监督超级解析的方法是将LR空间和HR空间作为两个域,使用循环中循环的结构来学习彼此之间的映射。在这种情况下,训练目标包括推动映射结果与目标域分布相匹配,并通过循环中映射使图像可恢复。在CycleGAN[138]的激励下,Yuan等人[131]提出了一个循环中的SR网络(CinCGAN),由4个生成器和2个判别器组成,分别为噪声LR⌦干净LR和干净LR⌦干净HR映射组成两个CycleGAN。具体来说,在第一个CycleGAN中,将有噪声的LR图像送入一个生成器中,要求输出的图像与真实的干净LR图像的分布一致。然后再送入另一个生成器,要求恢复原始输入。采用了几种损失函数(如对抗损失、周期一致性损失、身份损失)来保证周期一致性、分布一致性和映射有效性。另一种CycleGAN的设计类似,只是映射域不同。由于避免了预定义的退化,无监督的CinCGAN不仅能达到与监督方法相当的性能,而且即使在非常苛刻的条件下也能适用于各种情况。但由于SR问题的本质是不确定的,且CinCGAN的体系结构复杂,因此需要一些高级策略来降低训练难度和不稳定性。
4.3 深度图像先验
考虑到CNN结构足以捕获大量的低级图像统计先验,Ulyanov等[160]采用随机初始化的CNN作为手工制作的先验来执行SR。具体来说,他们定义了一个生成器网络,它以随机向量z作为输入,并尝试生成目标HR图像Iy。目标是训练网络找到一个ˆIy,使下采样的ˆIy与LR图像Ix相同。由于网络是随机初始化的,从未进行过训练,所以唯一的先验就是CNN结构本身。虽然这种方法的性能仍然比有监督的方法差(2dB),但它的性能大大优于传统的双立方上采样(1dB)。此外,这也说明了CNN架构本身的合理性,并提示我们将深度学习方法与CNN结构或自相似性等手工制作的前导结合起来改进SR。
参考文献
[1] H. Greenspan, “Super-resolution in medical imaging,” The Computer Journal, vol. 52, 2008.
[2] J. S. Isaac and R. Kulkarni, “Super resolution techniques for medical image processing,” in ICTSD, 2015.
[3] Y. Huang, L. Shao, and A. F. Frangi, “Simultaneous superresolution and cross-modality synthesis of 3d medical images using weakly-supervised joint convolutional sparse coding,” in CVPR, 2017.
[4] L. Zhang, H. Zhang, H. Shen, and P. Li, “A super-resolution reconstruction algorithm for surveillance images,” Elsevier Signal Processing, vol. 90, 2010.
[5] P. Rasti, T. Uiboupin, S. Escalera, and G. Anbarjafari, “Convolutional neural network super resolution for face recognition in surveillance monitoring,” in AMDO, 2016.
[6] D. Dai, Y. Wang, Y. Chen, and L. Van Gool, “Is image superresolution helpful for other vision tasks?” in WACV, 2016.
[7] M. Haris, G. Shakhnarovich, and N. Ukita, “Task-driven super resolution: Object detection in low-resolution images,” Arxiv:1803.11316, 2018.
[8] M. S. Sajjadi, B. Scholkopf, and M. Hirsch, “Enhancenet: Single ¨ image super-resolution through automated texture synthesis,” in ICCV, 2017.
[9] Y. Zhang, Y. Bai, M. Ding, and B. Ghanem, “Sod-mtgan: Small object detection via multi-task generative adversarial network,” in ECCV, 2018.
[10] R. Keys, “Cubic convolution interpolation for digital image processing,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 29, 1981.
[11] C. E. Duchon, “Lanczos filtering in one and two dimensions,” Journal of Applied Meteorology, vol. 18, 1979.
[12] M. Irani and S. Peleg, “Improving resolution by image registration,” CVGIP: Graphical Models and Image Processing, vol. 53, 1991.
[13] G. Freedman and R. Fattal, “Image and video upscaling from local self-examples,” TOG, vol. 30, 2011.
[14] J. Sun, Z. Xu, and H.-Y. Shum, “Image super-resolution using gradient profile prior,” in CVPR, 2008.
[15] K. I. Kim and Y. Kwon, “Single-image super-resolution using sparse regression and natural image prior,” TPAMI, vol. 32, 2010.
[16] Z. Xiong, X. Sun, and F. Wu, “Robust web image/video superresolution,” IEEE Transactions on Image Processing, vol. 19, 2010.
[17] W. T. Freeman, T. R. Jones, and E. C. Pasztor, “Examplebased super-resolution,” IEEE Computer Graphics and Applications, vol. 22, 2002.
[18] H. Chang, D.-Y. Yeung, and Y. Xiong, “Super-resolution through neighbor embedding,” in CVPR, 2004.
[19] D. Glasner, S. Bagon, and M. Irani, “Super-resolution from a single image,” in ICCV, 2009.
[20] Y. Jianchao, J. Wright, T. Huang, and Y. Ma, “Image superresolution as sparse representation of raw image patches,” in CVPR, 2008.
[21] J. Yang, J. Wright, T. S. Huang, and Y. Ma, “Image superresolution via sparse representation,” IEEE Transactions on Image Processing, vol. 19, 2010.
[22] C. Dong, C. C. Loy, K. He, and X. Tang, “Learning a deep convolutional network for image super-resolution,” in ECCV, 2014.
[23] ——, “Image super-resolution using deep convolutional networks,” TPAMI, vol. 38, 2016.
[24] I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. WardeFarley, S. Ozair, A. Courville, and Y. Bengio, “Generative adversarial nets,” in NIPS, 2014.
[25] C. Ledig, L. Theis, F. Huszar, J. Caballero, A. Cunningham, ´ A. Acosta, A. P. Aitken, A. Tejani, J. Totz, Z. Wang et al., “Photorealistic single image super-resolution using a generative adversarial network,” in CVPR, 2017.
[26] J. Kim, J. Kwon Lee, and K. Mu Lee, “Accurate image superresolution using very deep convolutional networks,” in CVPR, 2016.
[27] W.-S. Lai, J.-B. Huang, N. Ahuja, and M.-H. Yang, “Deep laplacian pyramid networks for fast and accurate superresolution,” in CVPR, 2017.
[28] N. Ahn, B. Kang, and K.-A. Sohn, “Fast, accurate, and lightweight super-resolution with cascading residual network,” in ECCV, 2018.
[29] J. Johnson, A. Alahi, and L. Fei-Fei, “Perceptual losses for realtime style transfer and super-resolution,” in ECCV, 2016.
[30] A. Bulat and G. Tzimiropoulos, “Super-fan: Integrated facial landmark localization and super-resolution of real-world low resolution faces in arbitrary poses with gans,” in CVPR, 2018.
[31] B. Lim, S. Son, H. Kim, S. Nah, and K. M. Lee, “Enhanced deep residual networks for single image super-resolution,” in CVPRW, 2017.
[32] Y. Wang, F. Perazzi, B. McWilliams, A. Sorkine-Hornung, O. Sorkine-Hornung, and C. Schroers, “A fully progressive approach to single-image super-resolution,” in CVPRW, 2018.
[33] S. C. Park, M. K. Park, and M. G. Kang, “Super-resolution image reconstruction: A technical overview,” IEEE Signal Processing Magazine, vol. 20, 2003.
[34] K. Nasrollahi and T. B. Moeslund, “Super-resolution: A comprehensive survey,” Machine Vision and Applications, vol. 25, 2014.
[35] J. Tian and K.-K. Ma, “A survey on super-resolution imaging,” Signal, Image and Video Processing, vol. 5, 2011.
[36] J. Van Ouwerkerk, “Image super-resolution survey,” Image and Vision Computing, vol. 24, 2006.
[37] C.-Y. Yang, C. Ma, and M.-H. Yang, “Single-image superresolution: A benchmark,” in ECCV, 2014.
[38] D. Thapa, K. Raahemifar, W. R. Bobier, and V. Lakshminarayanan, “A performance comparison among different super-resolution techniques,” Computers & Electrical Engineering, vol. 54, 2016.
[39] K. Zhang, W. Zuo, and L. Zhang, “Learning a single convolutional super-resolution network for multiple degradations,” in CVPR, 2018.
[40] D. Martin, C. Fowlkes, D. Tal, and J. Malik, “A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics,” in ICCV, 2001.
[41] P. Arbelaez, M. Maire, C. Fowlkes, and J. Malik, “Contour detection and hierarchical image segmentation,” TPAMI, vol. 33, 2011.
[42] E. Agustsson and R. Timofte, “Ntire 2017 challenge on single image super-resolution: Dataset and study,” in CVPRW, 2017.
[43] C. Dong, C. C. Loy, and X. Tang, “Accelerating the superresolution convolutional neural network,” in ECCV, 2016.
[44] R. Timofte, R. Rothe, and L. Van Gool, “Seven ways to improve example-based single image super resolution,” in CVPR, 2016.
[45] A. Fujimoto, T. Ogawa, K. Yamamoto, Y. Matsui, T. Yamasaki, and K. Aizawa, “Manga109 dataset and creation of metadata,” in MANPU, 2016.
[46] X. Wang, K. Yu, C. Dong, and C. C. Loy, “Recovering realistic texture in image super-resolution by deep spatial feature transform,” 2018.
[47] Y. Blau, R. Mechrez, R. Timofte, T. Michaeli, and L. Zelnik-Manor, “2018 pirm challenge on perceptual image super-resolution,” in ECCV Workshop, 2018.
[48] M. Bevilacqua, A. Roumy, C. Guillemot, and M. L. Alberi-Morel, “Low-complexity single-image super-resolution based on nonnegative neighbor embedding,” in BMVC, 2012.
[49] R. Zeyde, M. Elad, and M. Protter, “On single image scaleup using sparse-representations,” in International Conference on Curves and Surfaces, 2010.
[50] J.-B. Huang, A. Singh, and N. Ahuja, “Single image superresolution from transformed self-exemplars,” in CVPR, 2015.
[51] J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li, and L. Fei-Fei, “Imagenet: A large-scale hierarchical image database,” in CVPR, 2009.
[52] T.-Y. Lin, M. Maire, S. Belongie, J. Hays, P. Perona, D. Ramanan, P. Dollar, and C. L. Zitnick, “Microsoft coco: Common objects in ´ context,” in ECCV, 2014.
[53] M. Everingham, S. A. Eslami, L. Van Gool, C. K. Williams, J. Winn, and A. Zisserman, “The pascal visual object classes challenge: A retrospective,” IJCV, vol. 111, 2015.
[54] Z. Liu, P. Luo, X. Wang, and X. Tang, “Deep learning face attributes in the wild,” in ICCV, 2015.
[55] Y. Tai, J. Yang, X. Liu, and C. Xu, “Memnet: A persistent memory network for image restoration,” in ICCV, 2017.
[56] Y. Tai, J. Yang, and X. Liu, “Image super-resolution via deep recursive residual network,” in CVPR, 2017.
[57] M. Haris, G. Shakhnarovich, and N. Ukita, “Deep backp-rojection networks for super-resolution,” in CVPR, 2018.
[58] Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, “Image quality assessment: From error visibility to structural similarity,” IEEE Transactions on Image Processing, vol. 13, 2004.
[59] Z. Wang, A. C. Bovik, and L. Lu, “Why is image quality assessment so difficult?” in ICASSP, 2002.
[60] H. R. Sheikh, M. F. Sabir, and A. C. Bovik, “A statistical evaluation of recent full reference image quality assessment algorithms,” IEEE Transactions on Image Processing, vol. 15, 2006.
[61] Z. Wang and A. C. Bovik, “Mean squared error: Love it or leave it? a new look at signal fidelity measures,” IEEE Signal Processing Magazine, vol. 26, 2009.
[62] Z. Wang, D. Liu, J. Yang, W. Han, and T. Huang, “Deep networks for image super-resolution with sparse prior,” in ICCV, 2015.
[63] X. Xu, D. Sun, J. Pan, Y. Zhang, H. Pfister, and M.-H. Yang, “Learning to super-resolve blurry face and text images,” in ICCV, 2017.
[64] R. Dahl, M. Norouzi, and J. Shlens, “Pixel recursive super resolution,” in ICCV, 2017.
[65] W.-S. Lai, J.-B. Huang, N. Ahuja, and M.-H. Yang, “Fast and accurate image super-resolution with deep laplacian pyramid networks,” TPAMI, 2018.
[66] C. Ma, C.-Y. Yang, X. Yang, and M.-H. Yang, “Learning a noreference quality metric for single-image super-resolution,” Computer Vision and Image Understanding, 2017.
[67] H. Talebi and P. Milanfar, “Nima: Neural image assessment,” IEEE Transactions on Image Processing, vol. 27, 2018.
[68] J. Kim and S. Lee, “Deep learning of human visual sensitivity in image quality assessment framework,” in CVPR, 2017.
[69] R. Zhang, P. Isola, A. A. Efros, E. Shechtman, and O. Wang, “The unreasonable effectiveness of deep features as a perceptual metric,” in CVPR, 2018.
[70] Y. Zhang, K. Li, K. Li, L. Wang, B. Zhong, and Y. Fu, “Image super-resolution using very deep residual channel attention networks,” in ECCV, 2018.
[71] C. Fookes, F. Lin, V. Chandran, and S. Sridharan, “Evaluation of image resolution and super-resolution on face recognition performance,” Journal of Visual Communication and Image Representation, vol. 23, 2012.
[72] K. Zhang, Z. ZHANG, C.-W. Cheng, W. Hsu, Y. Qiao, W. Liu, and T. Zhang, “Super-identity convolutional neural network for face hallucination,” in ECCV, 2018.
[73] Y. Chen, Y. Tai, X. Liu, C. Shen, and J. Yang, “Fsrnet: End-to-end learning face super-resolution with facial priors,” in CVPR, 2018.
[74] Z. Wang, E. Simoncelli, A. Bovik et al., “Multi-scale structural similarity for image quality assessment,” in Asilomar Conference on Signals, Systems, and Computers, 2003.
[75] L. Zhang, L. Zhang, X. Mou, D. Zhang et al., “Fsim: a feature similarity index for image quality assessment,” IEEE transactions on Image Processing, vol. 20, 2011.
[76] A. Mittal, R. Soundararajan, and A. C. Bovik, “Making a completely blind image quality analyzer,” IEEE Signal Processing Letters, 2013.
[77] Y. Blau and T. Michaeli, “The perception-distortion tradeoff,” in CVPR, 2018.
[78] X. Mao, C. Shen, and Y.-B. Yang, “Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections,” in NIPS, 2016.
[79] T. Tong, G. Li, X. Liu, and Q. Gao, “Image super-resolution using dense skip connections,” in ICCV, 2017.
[80] R. Timofte, E. Agustsson, L. Van Gool, M.-H. Yang, L. Zhang, B. Lim, S. Son, H. Kim, S. Nah, K. M. Lee et al., “Ntire 2017 challenge on single image super-resolution: Methods and results,” in CVPRW, 2017.
[81] A. Ignatov, R. Timofte, T. Van Vu, T. Minh Luu, T. X Pham, C. Van Nguyen, Y. Kim, J.-S. Choi, M. Kim, J. Huang et al., “Pirm challenge on perceptual image enhancement on smartphones: report,” in ECCV Workshop, 2018.
[82] J. Kim, J. Kwon Lee, and K. Mu Lee, “Deeply-recursive convolutional network for image super-resolution,” in CVPR, 2016.
[83] A. Shocher, N. Cohen, and M. Irani, “zero-shot super-resolution using deep internal learning,” in CVPR, 2018.
[84] W. Shi, J. Caballero, F. Huszar, J. Totz, A. P. Aitken, R. Bishop, ´ D. Rueckert, and Z. Wang, “Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network,” in CVPR, 2016.
[85] W. Han, S. Chang, D. Liu, M. Yu, M. Witbrock, and T. S. Huang, “Image super-resolution via dual-state recurrent networks,” in CVPR, 2018.
[86] Z. Li, J. Yang, Z. Liu, X. Yang, G. Jeon, and W. Wu, “Feedback network for image super-resolution,” in CVPR, 2019.
[87] M. Haris, G. Shakhnarovich, and N. Ukita, “Recurrent backprojection network for video super-resolution,” in CVPR, 2019.
[88] R. Timofte, V. De Smet, and L. Van Gool, “A+: Adjusted anchored neighborhood regression for fast super-resolution,” in ACCV, 2014.
[89] S. Schulter, C. Leistner, and H. Bischof, “Fast and accurate image upscaling with super-resolution forests,” in CVPR, 2015.
[90] M. D. Zeiler, D. Krishnan, G. W. Taylor, and R. Fergus, “Deconvolutional networks,” in CVPRW, 2010.
[91] M. D. Zeiler and R. Fergus, “Visualizing and understanding convolutional networks,” in ECCV, 2014.
[92] A. Odena, V. Dumoulin, and C. Olah, “Deconvolution and checkerboard artifacts,” Distill, 2016.
[93] Y. Zhang, Y. Tian, Y. Kong, B. Zhong, and Y. Fu, “Residual dense network for image super-resolution,” in CVPR, 2018.
[94] H. Gao, H. Yuan, Z. Wang, and S. Ji, “Pixel transposed convolutional networks,” TPAMI, 2019.
[95] X. Hu, H. Mu, X. Zhang, Z. Wang, T. Tan, and J. Sun, “Meta-sr: A magnification-arbitrary network for super-resolution,” in CVPR, 2019.
[96] K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in CVPR, 2016.
[97] R. Timofte, V. De Smet, and L. Van Gool, “Anchored neighborhood regression for fast example-based super-resolution,” in ICCV, 2013.
[98] Z. Hui, X. Wang, and X. Gao, “Fast and accurate single image super-resolution via information distillation network,” in CVPR, 2018.
[99] J. Li, F. Fang, K. Mei, and G. Zhang, “Multi-scale residual network for image super-resolution,” in ECCV, 2018.
[100] H. Ren, M. El-Khamy, and J. Lee, “Image super resolution based on fusing multiple convolution neural networks,” in CVPRW, 2017.
[101] C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, and A. Rabinovich, “Going deeper with convolutions,” in CVPR, 2015.
[102] G. Huang, Z. Liu, L. Van Der Maaten, and K. Q. Weinberger, “Densely connected convolutional networks,” in CVPR, 2017.
[103] X. Wang, K. Yu, S. Wu, J. Gu, Y. Liu, C. Dong, C. C. Loy, Y. Qiao, and X. Tang, “Esrgan: Enhanced super-resolution generative adversarial networks,” in ECCV Workshop, 2018.
[104] J. Hu, L. Shen, and G. Sun, “Squeeze-and-excitation networks,” in CVPR, 2018.
[105] T. Dai, J. Cai, Y. Zhang, S.-T. Xia, and L. Zhang, “Second-order attention network for single image super-resolution,” in CVPR, 2019.
[106] Y. Zhang, K. Li, K. Li, B. Zhong, and Y. Fu, “Residual non-local attention networks for image restoration,” ICLR, 2019.
[107] K. Zhang, W. Zuo, S. Gu, and L. Zhang, “Learning deep cnn denoiser prior for image restoration,” in CVPR, 2017.
[108] S. Xie, R. Girshick, P. Dollar, Z. Tu, and K. He, “Aggregated ´ residual transformations for deep neural networks,” in CVPR, 2017.
[109] F. Chollet, “Xception: Deep learning with depthwise separable convolutions,” in CVPR, 2017.
[110] A. G. Howard, M. Zhu, B. Chen, D. Kalenichenko, W. Wang, T. Weyand, M. Andreetto, and H. Adam, “Mobilenets: Efficient convolutional neural networks for mobile vision applications,” Arxiv:1704.04861, 2017.
[111] A. van den Oord, N. Kalchbrenner, L. Espeholt, O. Vinyals, A. Graves et al., “Conditional image generation with pixelcnn decoders,” in NIPS, 2016.
[112] J. Najemnik and W. S. Geisler, “Optimal eye movement strategies in visual search,” Nature, vol. 434, 2005.
[113] Q. Cao, L. Lin, Y. Shi, X. Liang, and G. Li, “Attention-aware face hallucination via deep reinforcement learning,” in CVPR, 2017.
[114] K. He, X. Zhang, S. Ren, and J. Sun, “Spatial pyramid pooling in deep convolutional networks for visual recognition,” in ECCV, 2014.
[115] H. Zhao, J. Shi, X. Qi, X. Wang, and J. Jia, “Pyramid scene parsing network,” in CVPR, 2017.
[116] D. Park, K. Kim, and S. Y. Chun, “Efficient module based single image super resolution for multiple problems,” in CVPRW, 2018.
[117] I. Daubechies, Ten lectures on wavelets. SIAM, 1992.
[118] S. Mallat, A wavelet tour of signal processing. Elsevier, 1999.
[119] W. Bae, J. J. Yoo, and J. C. Ye, “Beyond deep residual learning for image restoration: Persistent homology-guided manifold simplification,” in CVPRW, 2017.
[120] T. Guo, H. S. Mousavi, T. H. Vu, and V. Monga, “Deep wavelet prediction for image super-resolution,” in CVPRW, 2017.
[121] H. Huang, R. He, Z. Sun, T. Tan et al., “Wavelet-srnet: A waveletbased cnn for multi-scale face super resolution,” in ICCV, 2017.
[122] P. Liu, H. Zhang, K. Zhang, L. Lin, and W. Zuo, “Multi-level wavelet-cnn for image restoration,” in CVPRW, 2018.
[123] T. Vu, C. Van Nguyen, T. X. Pham, T. M. Luu, and C. D. Yoo, “Fast and efficient image quality enhancement via desubpixel convolutional neural networks,” in ECCV Workshop, 2018.
[124] I. Kligvasser, T. Rott Shaham, and T. Michaeli, “xunit: Learning a spatial activation function for efficient image restoration,” in CVPR, 2018.
[125] A. Bruhn, J. Weickert, and C. Schnorr, “Lucas/kanade meets ¨ horn/schunck: Combining local and global optic flow methods,” IJCV, vol. 61, 2005.
[126] H. Zhao, O. Gallo, I. Frosio, and J. Kautz, “Loss functions for image restoration with neural networks,” IEEE Transactions on Computational Imaging, vol. 3, 2017.
[127] A. Dosovitskiy and T. Brox, “Generating images with perceptual similarity metrics based on deep networks,” in NIPS, 2016.
[128] K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” in ICLR, 2015.
[129] L. Gatys, A. S. Ecker, and M. Bethge, “Texture synthesis using convolutional neural networks,” in NIPS, 2015.
[130] L. A. Gatys, A. S. Ecker, and M. Bethge, “Image style transfer using convolutional neural networks,” in CVPR, 2016.
[131] Y. Yuan, S. Liu, J. Zhang, Y. Zhang, C. Dong, and L. Lin, “Unsupervised image super-resolution using cycle-in-cycle generative adversarial networks,” in CVPRW, 2018.
[132] X. Mao, Q. Li, H. Xie, R. Y. Lau, Z. Wang, and S. P. Smolley, “Least squares generative adversarial networks,” in ICCV, 2017.
[133] S.-J. Park, H. Son, S. Cho, K.-S. Hong, and S. Lee, “Srfeat: Single image super resolution with feature discrimination,” in ECCV, 2018.
[134] A. Jolicoeur-Martineau, “The relativistic discriminator: a key element missing from standard gan,” Arxiv:1807.00734, 2018.
[135] M. Arjovsky, S. Chintala, and L. Bottou, “Wasserstein generative adversarial networks,” in ICML, 2017.
[136] I. Gulrajani, F. Ahmed, M. Arjovsky, V. Dumoulin, and A. C. Courville, “Improved training of wasserstein gans,” in NIPS, 2017.
[137] T. Miyato, T. Kataoka, M. Koyama, and Y. Yoshida, “Spectral normalization for generative adversarial networks,” in ICLR, 2018.
[138] J.-Y. Zhu, T. Park, P. Isola, and A. A. Efros, “Unpaired image-toimage translation using cycle-consistent adversarial networks,” in ICCV, 2017.
[139] L. I. Rudin, S. Osher, and E. Fatemi, “Nonlinear total variation based noise removal algorithms,” Physica D: Nonlinear Phenomena, vol. 60, 1992.
[140] H. A. Aly and E. Dubois, “Image up-sampling using totalvariation regularization with a new observation model,” IEEE Transactions on Image Processing, vol. 14, 2005.
[141] Y. Guo, Q. Chen, J. Chen, J. Huang, Y. Xu, J. Cao, P. Zhao, and M. Tan, “Dual reconstruction nets for image super-resolution with gradient sensitive loss,” arXiv:1809.07099, 2018.
[142] S. Vasu, N. T. Madam et al., “Analyzing perception-distortion tradeoff using enhanced perceptual super-resolution network,” in ECCV Workshop, 2018.
[143] M. Cheon, J.-H. Kim, J.-H. Choi, and J.-S. Lee, “Generative adversarial network-based image super-resolution using perceptual content losses,” in ECCV Workshop, 2018.
[144] J.-H. Choi, J.-H. Kim, M. Cheon, and J.-S. Lee, “Deep learningbased image super-resolution considering quantitative and perceptual quality,” in ECCV Workshop, 2018.
[145] I. Sergey and S. Christian, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in ICML, 2015.
[146] C. K. Sønderby, J. Caballero, L. Theis, W. Shi, and F. Huszar, ´ “Amortised map inference for image super-resolution,” in ICLR, 2017.
[147] R. Chen, Y. Qu, K. Zeng, J. Guo, C. Li, and Y. Xie, “Persistent memory residual network for single image super resolution,” in CVPRW, 2018.
[148] Y. Bengio, J. Louradour, R. Collobert, and J. Weston, “Curriculum learning,” in ICML, 2009.
[149] Y. Bei, A. Damian, S. Hu, S. Menon, N. Ravi, and C. Rudin, “New techniques for preserving global structure and denoising with low information loss in single-image super-resolution,” in CVPRW, 2018.
[150] N. Ahn, B. Kang, and K.-A. Sohn, “Image super-resolution via progressive cascading residual network,” in CVPRW, 2018.
[151] T. Karras, T. Aila, S. Laine, and J. Lehtinen, “Progressive growing of gans for improved quality, stability, and variation,” in ICLR, 2018.
[152] R. Caruana, “Multitask learning,” Machine Learning, vol. 28, 1997.
[153] K. He, G. Gkioxari, P. Dollar, and R. Girshick, “Mask r-cnn,” in ´ ICCV, 2017.
[154] Z. Zhang, P. Luo, C. C. Loy, and X. Tang, “Facial landmark detection by deep multi-task learning,” in ECCV, 2014.
[155] X. Wang, K. Yu, C. Dong, X. Tang, and C. C. Loy, “Deep network interpolation for continuous imagery effect transition,” in CVPR, 2019.
[156] J. Caballero, C. Ledig, A. P. Aitken, A. Acosta, J. Totz, Z. Wang, and W. Shi, “Real-time video super-resolution with spatiotemporal networks and motion compensation,” in CVPR, 2017.
[157] L. Zhu, “pytorch-opcounter,” https://github.com/Lyken17/pytorchOpCounter, 2019.
[158] T. Michaeli and M. Irani, “Nonparametric blind superresolution,” in ICCV, 2013.
[159] A. Bulat, J. Yang, and G. Tzimiropoulos, “To learn image superresolution, use a gan to learn how to do image degradation first,” in ECCV, 2018.
[160] D. Ulyanov, A. Vedaldi, and V. Lempitsky, “Deep image prior,” in CVPR, 2018.
[161] J. Shotton, A. Fitzgibbon, M. Cook, T. Sharp, M. Finocchio, R. Moore, A. Kipman, and A. Blake, “Real-time human pose recognition in parts from single depth images,” in CVPR, 2011.
[162] G. Moon, J. Yong Chang, and K. Mu Lee, “V2v-posenet: Voxel-tovoxel prediction network for accurate 3d hand and human pose estimation from a single depth map,” in CVPR, 2018.
[163] S. Gupta, R. Girshick, P. Arbelaez, and J. Malik, “Learning rich ´ features from rgb-d images for object detection and segmentation,” in ECCV, 2014.
[164] W. Wang and U. Neumann, “Depth-aware cnn for rgb-d segmentation,” in ECCV, 2018.
[165] X. Song, Y. Dai, and X. Qin, “Deep depth super-resolution: Learning depth super-resolution using deep convolutional neural network,” in ACCV, 2016.
[166] T.-W. Hui, C. C. Loy, and X. Tang, “Depth map super-resolution by deep multi-scale guidance,” in ECCV, 2016.
[167] B. Haefner, Y. Queau, T. M ´ ollenhoff, and D. Cremers, “Fight ¨ ill-posedness with ill-posedness: Single-shot variational depth super-resolution from shading,” in CVPR, 2018.
[168] G. Riegler, M. Ruther, and H. Bischof, “Atgv-net: Accurate depth ¨ super-resolution,” in ECCV, 2016.
[169] J.-S. Park and S.-W. Lee, “An example-based face hallucination method for single-frame, low-resolution facial images,” IEEE Transactions on Image Processing, vol. 17, 2008.
[170] S. Zhu, S. Liu, C. C. Loy, and X. Tang, “Deep cascaded bi-network for face hallucination,” in ECCV, 2016.
[171] X. Yu, B. Fernando, B. Ghanem, F. Porikli, and R. Hartley, “Face super-resolution guided by facial component heatmaps,” in ECCV, 2018.
[172] X. Yu and F. Porikli, “Face hallucination with tiny unaligned images by transformative discriminative neural networks,” in AAAI, 2017.
[173] M. Jaderberg, K. Simonyan, A. Zisserman et al., “Spatial transformer networks,” in NIPS, 2015.
[174] X. Yu and F. Porikli, “Hallucinating very low-resolution unaligned and noisy face images by transformative discriminative autoencoders,” in CVPR, 2017.
[175] Y. Song, J. Zhang, S. He, L. Bao, and Q. Yang, “Learning to hallucinate face images via component generation and enhancement,” in IJCAI, 2017.
[176] C.-Y. Yang, S. Liu, and M.-H. Yang, “Hallucinating compressed face images,” IJCV, vol. 126, 2018.
[177] X. Yu and F. Porikli, “Ultra-resolving face images by discriminative generative networks,” in ECCV, 2016.
[178] C.-H. Lee, K. Zhang, H.-C. Lee, C.-W. Cheng, and W. Hsu, “Attribute augmented convolutional neural network for face hallucination,” in CVPRW, 2018.
[179] X. Yu, B. Fernando, R. Hartley, and F. Porikli, “Super-resolving very low-resolution face images with supplementary attributes,” in CVPR, 2018.
[180] M. Mirza and S. Osindero, “Conditional generative adversarial nets,” Arxiv:1411.1784, 2014.
[181] M. Fauvel, Y. Tarabalka, J. A. Benediktsson, J. Chanussot, and J. C. Tilton, “Advances in spectral-spatial classification of hyperspectral images,” Proceedings of the IEEE, vol. 101, 2013.
[182] Y. Fu, Y. Zheng, I. Sato, and Y. Sato, “Exploiting spectral-spatial correlation for coded hyperspectral image restoration,” in CVPR, 2016.
[183] B. Uzkent, A. Rangnekar, and M. J. Hoffman, “Aerial vehicle tracking by adaptive fusion of hyperspectral likelihood maps,” in CVPRW, 2017.
[184] G. Masi, D. Cozzolino, L. Verdoliva, and G. Scarpa, “Pansharpening by convolutional neural networks,” Remote Sensing, vol. 8, 2016.
[185] Y. Qu, H. Qi, and C. Kwan, “Unsupervised sparse dirichlet-net for hyperspectral image super-resolution,” in CVPR, 2018.
[186] Y. Fu, T. Zhang, Y. Zheng, D. Zhang, and H. Huang, “Hyperspectral image super-resolution with optimized rgb guidance,” in CVPR, 2019.
[187] C. Chen, Z. Xiong, X. Tian, Z.-J. Zha, and F. Wu, “Camera lens super-resolution,” in CVPR, 2019.
[188] X. Zhang, Q. Chen, R. Ng, and V. Koltun, “Zoom to learn, learn to zoom,” in CVPR, 2019.
[189] X. Xu, Y. Ma, and W. Sun, “Towards real scene super-resolution with raw images,” in CVPR, 2019.
[190] R. Liao, X. Tao, R. Li, Z. Ma, and J. Jia, “Video super-resolution via deep draft-ensemble learning,” in ICCV, 2015.
[191] A. Kappeler, S. Yoo, Q. Dai, and A. K. Katsaggelos, “Video superresolution with convolutional neural networks,” IEEE Transactions on Computational Imaging, vol. 2, 2016.
[192] ——, “Super-resolution of compressed videos using convolutional neural networks,” in ICIP, 2016.
[193] M. Drulea and S. Nedevschi, “Total variation regularization of local-global optical flow,” in ITSC, 2011.
[194] D. Liu, Z. Wang, Y. Fan, X. Liu, Z. Wang, S. Chang, and T. Huang, “Robust video super-resolution with learned temporal dynamics,” in ICCV, 2017.
[195] D. Liu, Z. Wang, Y. Fan, X. Liu, Z. Wang, S. Chang, X. Wang, and T. S. Huang, “Learning temporal dynamics for video superresolution: A deep learning approach,” IEEE Transactions on Image Processing, vol. 27, 2018.
[196] X. Tao, H. Gao, R. Liao, J. Wang, and J. Jia, “Detail-revealing deep video super-resolution,” in ICCV, 2017.
[197] Y. Huang, W. Wang, and L. Wang, “Bidirectional recurrent convolutional networks for multi-frame super-resolution,” in NIPS, 2015.
[198] ——, “Video super-resolution via bidirectional recurrent convolutional networks,” TPAMI, vol. 40, 2018.
[199] J. Guo and H. Chao, “Building an end-to-end spatial-temporal convolutional network for video super-resolution,” in AAAI, 2017.
[200] A. Graves, S. Fernandez, and J. Schmidhuber, “Bidirectional lstm ´ networks for improved phoneme classification and recognition,” in ICANN, 2005.
[201] M. S. Sajjadi, R. Vemulapalli, and M. Brown, “Frame-recurrent video super-resolution,” in CVPR, 2018.
[202] S. Li, F. He, B. Du, L. Zhang, Y. Xu, and D. Tao, “Fast spatiotemporal residual network for video super-resolution,” in CVPR, 2019.
[203] Z. Zhang and V. Sze, “Fast: A framework to accelerate superresolution processing on compressed videos,” in CVPRW, 2017.
[204] Y. Jo, S. W. Oh, J. Kang, and S. J. Kim, “Deep video superresolution network using dynamic upsampling filters without explicit motion compensation,” in CVPR, 2018.
[205] J. Li, X. Liang, Y. Wei, T. Xu, J. Feng, and S. Yan, “Perceptual generative adversarial networks for small object detection,” in CVPR, 2017.
[206] W. Tan, B. Yan, and B. Bare, “Feature super-resolution: Make machine see more clearly,” in CVPR, 2018.
[207] D. S. Jeon, S.-H. Baek, I. Choi, and M. H. Kim, “Enhancing the spatial resolution of stereo images using a parallax prior,” in CVPR, 2018.
[208] L. Wang, Y. Wang, Z. Liang, Z. Lin, J. Yang, W. An, and Y. Guo, “Learning parallax attention for stereo image super-resolution,” in CVPR, 2019.
[209] Y. Li, V. Tsiminaki, R. Timofte, M. Pollefeys, and L. V. Gool, “3d appearance super-resolution with deep learning,” in CVPR, 2019.
[210] S. Zhang, Y. Lin, and H. Sheng, “Residual networks for light field image super-resolution,” in CVPR, 2019.
[211] C. Ancuti, C. O. Ancuti, R. Timofte, L. Van Gool, L. Zhang, M.- H. Yang, V. M. Patel, H. Zhang, V. A. Sindagi, R. Zhao et al., “Ntire 2018 challenge on image dehazing: Methods and results,” in CVPRW, 2018.
[212] H. Pham, M. Y. Guan, B. Zoph, Q. V. Le, and J. Dean, “Efficient neural architecture search via parameter sharing,” in ICML, 2018.
[213] H. Liu, K. Simonyan, and Y. Yang, “Darts: Differentiable architecture search,” ICLR, 2019.
[214] Y. Guo, Y. Zheng, M. Tan, Q. Chen, J. Chen, P. Zhao, and J. Huang, “Nat: Neural architecture transformer for accurate and compact architectures,” in NIPS, 2019, pp. 735–747.