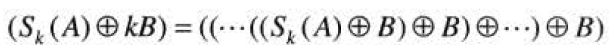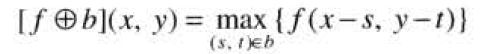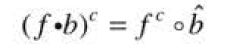数字图像处理第九章笔记——形态学图像处理

目录

引言

一、预备知识

1.1 平移与反射

1.2 结构元

二、 腐蚀和膨胀

2.1 腐蚀

2.2 膨胀 

2.3 对偶性 

2.4 python实现腐蚀和膨胀

三、开操作和闭操作

四、 击中或击不中变换 

五、基本的形态学算法 

5.1 边界提取

5.2 孔洞填充 

5.3 连通分量的提取 

5.4 凸壳

5.5 细化

5.6 粗化 

5.7 骨架

六、灰度级形态学 

6.1 腐蚀和膨胀 

6.2 开操作和闭操作 

七、总结

---

引言

        这里的形态学并非指生物学的那一个分支，而是数学形态学的内容，将数学形态学作为工具从图像中提取表达和描绘区域形状的有用图像分量，如边界、骨架和凸壳等。这一章学习将从输入输出均为图像的图像处理转为输入是图像输出是这些图像中提取属性的处理。类似形态学及与其相关概念这样的工具数学基础的基石，用于提取图像中的内涵。

一、预备知识

1.1 平移与反射

        数学形态学的语言是集合论，同样的，形态学为大量的图像处理问题提供了一种一致且有力的方法。在数学形态学中的集合其内部的元素不再是传统意义上的数字，它表示的是图像中的对象。以二值图像为例，所有的白色像素的集合就是该图像的一个完整的形态学描述。在二值图像中的集合是二维整数空间的元素，在这个集合中每一个元素就是一个多元组(即二维向量)，这些多元组的是图像中一个像素的坐标(x,y)。

        集合的反射和平移定义的概念在形态学中的应用也很广泛，这里令集合B的反射表示为，并将其定义为：

在上式的作用下，为此若B中元素坐标为(x,y)，则中对应元素的坐标就是(-x,-y)。用图来表示就是如下：

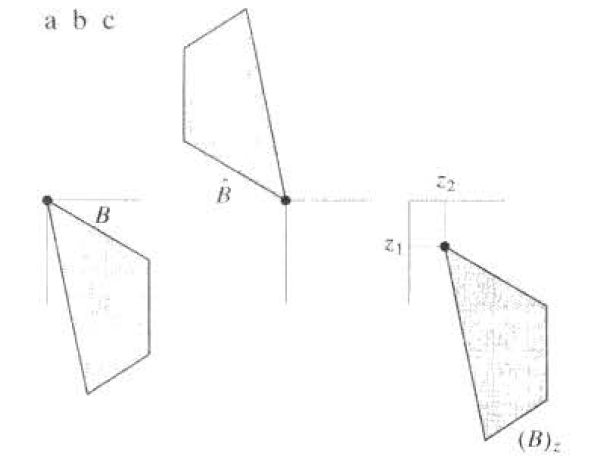
        集合B按照点(z1,z2)表示为(B)的平移定义如下：

(B) = { c | c = b + z , b  B} 

由上式的描述我们就能够得知(B)就是B中(x,y)被(x+z1,y+z2)替代的点的集合，上图的c与a的对比可以完美的展示图像的变换。

1.2 结构元

        所谓结构元就是一个形状和大小已知的像素点集，通常还要为结构元定义一个中心。数学形态学运算是在结构元作用下进行的，利用它与二值图像对应的区域进行特定的逻辑运算。在图像中不断移动结构元，就可以考察图像之间各部分的关系，其形状、尺寸的选择决定了数学形态学运算的效果。

结构元选择的主要原则是：

1、结构元在几何上必须比原图像简单，且有界。

2、在多尺度形态学分析中，结构元的大小可以变化。但结构元的尺寸一般要明显小于目标图像的尺寸。

3、结构元的凸性很重要．保证连接两点的线段位于集合的内部。

4、根据不同的图像分析目的，常用的结构元有方形、扁平形、圆形等。

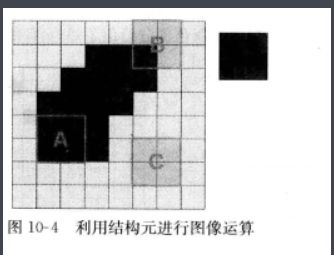
        上图的A,B,C给出了简单的结构元模型。在形态学中集合的反射和平移广泛用来表达基于结构元的操作。涂阴影的方块表示结构元的一个成员，当给定结构元中的一个位置与该结构元集合无关时就表示一个“不关心”条件。在对图像进行操作时，通常要求结构元的矩形阵列，通过给阴影部分添加最小可能数量的背景元素从而形成一个矩形来实现。下图为一个例子。

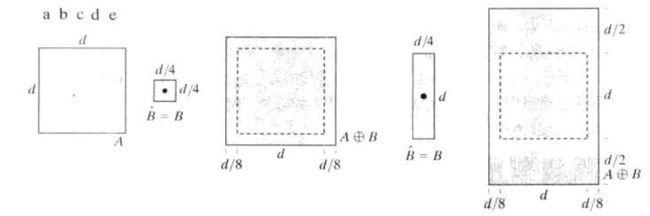
        在考虑结构元如何使用时，我们可以借助下图在表达，下图A为一个集合，B为一个结构元，正如先前所说要将其拓展为一个矩形，故对A,B进行拓展，得到下面的两个矩形结构。 

        将B置于A中进行平移运动，当A中阴影部分能够完全遮住B时，以B原点作为新集合成员。得到的结果就如图e中带有灰色划线的部分，这一操作又称为腐蚀，即消除了原本图像的边缘部分，在下面的部分里仍会讲到。 

二、 腐蚀和膨胀

2.1 腐蚀

        集合A和B都在中，B对A的腐蚀表示为，定义为：

该式指出了B对A的腐蚀是一个用z平移的B包含在A中的所有的点z的集合。我们假设B是一个结构元，从上面对结构元的描述我们知道了B不与A共享公共元素。由此可以将公式等价为：

其中为A的补集，为空集。 

腐蚀的一个例子 

        当我们使用上面的B作为结构元对A进行操作时得到的便是c展示的正方形，当使用下面的B对A进行操作时，得到的将是e展示的一条横线。由此我们知道腐蚀缩小细化了二值图像长得物体，我们也可以将腐蚀看成是形态学滤波操作。

2.2 膨胀 

集合A和B都在中，B对A的膨胀表示为，定义为：

这个公式是以B关于它的原点的映像，并且以z对映像进行平移为基础的，与腐蚀相反，B对A的膨胀是所有位移z的集合，因此(B)和A至少是有一个元素是重叠的，上式也可以等价为：

前面提及的腐蚀是一种细化或收缩操作，而膨胀则会“增长”或“粗化”二值图像中的物体，通过下图可以清晰的了解。

2.3 对偶性 

        膨胀和腐蚀彼此之间关于集合求补运算和反射运算是对偶的即：

B对A的腐蚀是对的膨胀的补，反之亦然。当结构元关于其原点对称时有： =B。

2.4 python实现腐蚀和膨胀

腐蚀操作：

import cv2
import matplotlib.pyplot as plt
import numpy as np

img = cv2.imread('D:\\picture\\test.jpg', 0)
kernel = np.ones((5, 5), np.uint8)

fushi = cv2.erode(img, kernel)

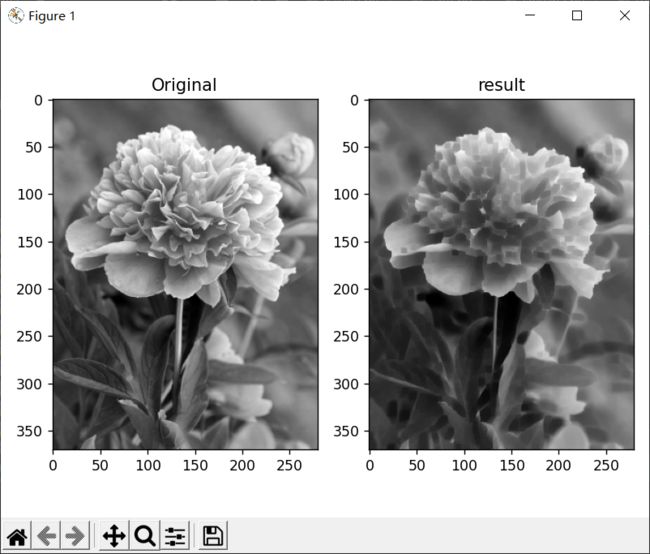
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('Original')
plt.subplot(122), plt.imshow(fushi, 'gray'), plt.title('result')
plt.tight_layout()
plt.show()

膨胀操作：

import cv2
import matplotlib.pyplot as plt
import numpy as np

img = cv2.imread('D:\\picture\\test.jpg', 0)
kernel = np.ones((5, 5), np.uint8)

pengzhang = cv2.dilate(img, kernel)

plt.subplot(121), plt.imshow(img, 'gray'), plt.title('Original')
plt.subplot(122), plt.imshow(pengzhang, 'gray'), plt.title('result')
plt.tight_layout()
plt.show()

从实验中可以看出，腐蚀后的图片会出现一定程度的细化，而膨胀后的图片则会出现粗化的现象。 

三、开操作和闭操作

        膨胀会扩大一幅图像的组成部分，而腐蚀则会缩小一幅图像中的组成部分。这里我们要学习开操作与闭操作。开操作一般会平滑物体的轮廓，断开较窄的狭颈并消除细的突出物。闭操作同样也会平滑轮廓的一部分，但与开操作相反，它通常会弥合较窄的间断和细长的沟壑，消除小的孔洞,填补轮廓线中的断裂。

开操作
        结构元B对集合A的开操作可以表示为：,其定义如下：

因此B对A的开操作就是B对A的腐蚀，紧接着用B对结果进行膨胀。

闭操作

        类似的，结构元B对集合A进行闭操作表示为 ，定义为：

则B对集合A的闭操作就是B对A膨胀，接着对结果进行腐蚀。

        假设将结构元B视为一个“转球”。然后， 的边界由B中的点建立：B在A的边界内侧滚动时，B能到达的A的边界的最远点。这里就可以将开操作表示为一个拟合处理：

这里的表示大括号内所有集合的并集。可以通过下图得到更为清晰的理解：

        就如同开操作的几何解释那般，闭操作同样有类似的几何操作。将结构元置于几何A的外部边界进行滚动操作，就可以得到最后的结果，具体可以观察下图：

        开操作与闭操作与腐蚀和膨胀之间有着千丝万缕的关系，下面的图可以让我们更好的对这四种方法加以理解。 

        第一行为集合A；第二行为利用B对A进行腐蚀操作；第三行是开操作，在第二行腐蚀的结果上进行膨胀；第四行是B对A进行膨胀；第五行便是闭操作，在第四行膨胀的结果上进行腐蚀。

四、 击中或击不中变换 

        形态学击中或击不中变换是形状检测的一个基本工具，借助下图对该概念加以说明。

        在上图中，集合A是由三种形状组成，分别为C、D、E ，每种形状的原点位于其重点处，图b显示了D被一个小窗口W包围的情况，将D与W之间的部分称为集合差(W-D)。图c则是集合A在矩形框下的补集。图d表示了利用D对A进行腐蚀后产生的集合，此时D完全包含于A中，在每个这样的位置D找到A中的一个击中。

        图e显示了局部背景集合(W-D)对A的补集的腐蚀，方框外部的阴影部分就是腐蚀区域，由图d和e可以看到，D精确地拟合A内部的位置集合是由D对A的腐蚀和(W-D)对A的腐蚀的交集，就如图f所示那般，这个交集就是我们需要寻找的位置。亦或者，若B表示由D及其背景组成的集合,则B在A中的匹配就表示为

       这个公式就可以被称为形态学击中或击不中变换。

五、基本的形态学算法 

5.1 边界提取

        集合A的边界可以通过先用B对A的腐蚀，然后求A和腐蚀结果至今的集合差得到：

B为一个结构元。

使用python进行实验模拟，二进制1为白色，二进制0为黑色，结果就下图所示。

img = cv2.imread('D:\\picture\\test.jpg',0)
kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (3, 3))
img_erode = cv2.erode(img, kernel)
result = img - img_erode
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('original')
plt.subplot(122), plt.imshow(result, 'gray'), plt.title('result')
plt.tight_layout()
plt.show()

结果图可以看出灰度变换后图片的轮廓。 

5.2 孔洞填充 

        孔洞可以被定义为由前景像素相连接的边界所包围的一个背景区域。令A表示一个集合，其元素是8连通的边界，每个边界包围一个背景区域，当给定每个孔洞一个点后，目的就是用1填充所有的孔洞。

        除了在每一个孔洞中对应于中的位置给定的点外，这一点已经被置1了，从形成一个由0组成的阵列开始，用如下过程使得1填充所有的孔洞

        若左边不加限制，则膨胀将填充整个区域。下图就是孔洞填充的例子。

5.3 连通分量的提取 

        在前面的章节里有学习过连通性和连通分量，从二值图像中提取连通分量是许多自动图像分析应用的核心，令A是包含一个或多个连通分量的集合，并形成一个阵列，除了对应于A中每个连通分量中的一个点的已知的每一个位置处我们已经置1外，该阵列的所有其他元素均为0，可由下面的迭代过程达到这个目的：

                

        B是一个适当的结构元，当时，该迭代过程结束，包含输入图像重点所有的连通分量。

        观察上图以及公式得到，连通分量的提取，选择起点为目标元素上的一个点，膨胀后再与A取交集。

5.4 凸壳

        集合A内连接任意两个点的直线段都在A的内部，则称集合A的凸形的。任意集合S的凸壳H是包含于S的最小凸集。集合差H-S称为S的凸缺。

        令，i=1,2,3,4表示下图的4个结构元，执行过程为：

，当 即过程收敛时，令，此时A的凸壳为：

        上图说明了两个公式的给出过程。图a给出了用于提取凸壳的结构元，原点再其中心处，x表示“不考虑”的条件。图b为集合A，从开始，经过公式的4次迭代，可以得到图c，之后令，再次使用公式就可以得到图d的集合。下面的图是以同样的方式得到的。

5.5 细化

        细化分为两步过程，第一步是正常的腐蚀，但那些被标为可除去的像素点不立即消去，第二步将那些消除后并不破坏连通性的点消除，否则保留。细化将一个曲线形物体细化为一条单像素宽的线，从而图形化地显示出其拓扑性质。

结构元对于集合A的细化可以表示为，由击中或击不中变换来定义时：

针对对称地细化A的一种更有用的表达方式是以结构元序列为基础的：

其中 是旋转后的形式。为此可以将细化公式重新定义为：

该式的意思是A被不断细化，直到得到的结果不再发生变化。

5.6 粗化 

        粗化是细化的形态学对偶，定义如下：

与细化一样粗化也可以定义为一个系列操作：

可提取图像的补并用细化运算处理背景。实际上当每种腐蚀的变形作用于一幅图像的补时，就会获得一种相应的膨胀型运算。

粗化可在不合并彼此分离的物体的前提下扩大边界。

5.7 骨架

        集合A的骨架概念直观上很简单，可以根据上图得到：

        1、如果z是S(A)的一个点，并且，是A内以z为中心的最大圆盘，则不存在包含，且位于A内的更大圆盘(不必以z为中心)。圆盘称为最大圆盘。

        2、圆盘在两个或多个不同的位置与A的边界接触。

集合A的骨架可以用腐蚀和开操作来表达：

B为一个适当的结构元，表示对A的连续k次腐蚀。

        此外可以通过下式重建骨架化的集合A：

其中 表示对的k次连续膨胀即

六、灰度级形态学 

        这一节里将膨胀、腐蚀、开操作和闭操作的基本操作扩展到灰度级图像。这里将对f(x,y)和b(x,y)进行处理，其中f(x,y)是一幅灰度级图像，b(x,y)则是一个结构元。灰度级形态学中的结构元所执行的基本功能与二值形态学中所对应的功能相同:它们作为一个“探测器”以明确的特性检验一幅给定的图像。灰度级形态学中的结构元属于两类:非平坦的和平坦的结构元。

6.1 腐蚀和膨胀 

腐蚀

        b的原点位于(x,y)处时，用一个平坦的结构元b在(x,y)处对图像f的腐蚀定义为图像f中与b重合区域的最小值。可以由以下公式给出：

 膨胀 

        当的原点位于(x,y)处时，平坦结构元b在任何位置(x,y)处对图像f的膨胀，就定义为图形f与重合区域的最大值。可以由以下公式给出：

先前在二值图像处的腐蚀和膨胀知识点介绍了python实现的结果，这里不再讨论。

6.2 开操作和闭操作 

        灰度级图像的开操作和闭操作的表达式与二值图像的对应操作具有相同的形式。

开操作：

闭操作：

灰度级图像的开操作和闭操作关于函数的补集和结构元的反射是对偶：

，所以上式也可以写成 

python对其进行实现可获得：

import cv2
import matplotlib.pyplot as plt

def open_image(image):
    ret, binary = cv2.threshold(image, 0, 255, cv2.THRESH_BINARY | cv2.THRESH_OTSU)
    kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (5, 5))  # 返回指定形状和尺寸的结构元素。
    binary = cv2.morphologyEx(binary, cv2.MORPH_OPEN, kernel)
    return binary


def close_image(image):
    ret, binary = cv2.threshold(image, 0, 255, cv2.THRESH_BINARY | cv2.THRESH_OTSU)
    kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (5, 5))
    binary = cv2.morphologyEx(binary, cv2.MORPH_CLOSE, kernel)
    return binary


img = cv2.imread("D:\\picture\\test2.jpg")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
open_p = open_image(gray)
close_p = close_image(gray)
plt.subplot(221), plt.imshow(img, 'gray'), plt.title('Original')
plt.subplot(222), plt.imshow(gray, 'gray'), plt.title('gray')
plt.subplot(223), plt.imshow(open_p, 'gray'), plt.title('open')
plt.subplot(224), plt.imshow(close_p, 'gray'), plt.title('close')
plt.tight_layout()
plt.show()

这里对于灰度图像进行了开操作与闭操作的处理，可以看出开操作，会平滑物体轮廓，断开较窄的狭颈，并消除细小的突出物。而闭操作，一般也会平滑物体轮廓，但与开操作相反，弥合较窄的间断和细长的沟壑，消除小的空洞，填补轮廓线的中的断裂。 

七、总结

主要学习了图像形态学的相关操作，由二值图像的腐蚀、膨胀以及开操作闭操作等转向灰度图像的腐蚀、膨胀、开操作闭操作等。