混淆电路的优化:P&P、Free XOR、GRR2
前置文章:https://blog.csdn.net/weixin_44885334/article/details/126557573
文献:
- Beaver D, Micali S, Rogaway P. The round complexity of secure protocols[C]//Proceedings of the twenty-second annual ACM symposium on Theory of computing. 1990: 503-513.
- Kolesnikov V, Schneider T. Improved garbled circuit: Free XOR gates and applications[C]//International Colloquium on Automata, Languages, and Programming. Springer, Berlin, Heidelberg, 2008: 486-498.
- Pinkas B, Schneider T, Smart N P, et al. Secure two-party computation is practical[C]//International conference on the theory and application of cryptology and information security. Springer, Berlin, Heidelberg, 2009: 250-267.
- Yakoubov S. A gentle introduction to Yao’s Garbled circuits[J]. preprint on webpage at https://web.mit.edu/sonka89/www/papers/2017ygc.pdf, 2017.
P&P
P&P技术(point-and-permute technique)是由 Beaver 等人在1990年提出的。利用这个技术,可以不必对混淆真值表的 4 4 4个条目都尝试解密,而是直接确定要解密哪一个条目。
原始论文的描述
Beaver 等人在文章中使用了 PRF、PRG、掷硬币协议、可验证的秘密共享方案、零知识证明、一次一密。对于 W W W根线和 n n n个人,先掷硬币生成 n × 2 W n \times 2W n×2W个私有种子(seeds)和随机比特,而人们的种子的 n n n级联作为某根线上的超级种子(super-seeds),每根线上两个超级种子(位置0和位置1)。用 PRG 根据私有种子来生成线标签(wire-labels),根据随机比特利用秘密共享将选择 2 2 2个超级种子中的一个作为混淆输入( garbled input),使用一次一密用输入线标签来加密输出线标签得到门标签( gate-labels)。根据线标签和种子的对应关系(利用PRG),从混淆输入(一个超级种子,包含一些种子)中得到超级种子的位置信息(0或1),然后只解密两根输入线的位置 ( p , q ) ∈ { 0 , 1 } 2 (p,q) \in \{0,1\}^2 (p,q)∈{0,1}2锁定的一个条目即可。
简化的描述
上述的描述特别繁琐。下面提取精华思想,重新描述一遍。
对于每一根电线,除了分配两个标签 k i 0 , k i 1 ∈ { 0 , 1 } n k_i^0,k_i^1 \in \{0,1\}^n ki0,ki1∈{0,1}n,额外再分配两个选择比特(select bits) p i 0 , p i 1 p_i^0,p_i^1 pi0,pi1:随机选择 r ∈ { 0 , 1 } r \in \{0,1\} r∈{0,1},令 p i v = v ⊕ r p_i^v = v \oplus r piv=v⊕r。于是针对不同的 v ∈ { 0 , 1 } v \in \{0,1\} v∈{0,1}选择比特 p i v p_i^v piv也不同,同时 p i v p_i^v piv也不会泄露 v v v的任何信息。
当然,对于电路输出线,后续就没有其他的逻辑门了,因此不需要分配选择比特。为了保持描述的一致性,我们记做 k o v ∥ ⊥ k_o^v \| \perp kov∥⊥。
不再需要特殊的 elusive range 的对称加密,P&P技术下只需要一个普通的对称加密方案 E n c , D e c Enc,Dec Enc,Dec,以及密钥派生函数(key derivation function) H H H。
对于门 g g g,假设它的输入线是 i , j i,j i,j,输出线是 l l l,那么将逻辑输出 g ( v i , v j ) g(v_i,v_j) g(vi,vj) 对应的 k l g ( v i , v j ) ∥ p l g ( v i , v j ) k_l^{g(v_i,v_j)} \| p_l^{g(v_i,v_j)} klg(vi,vj)∥plg(vi,vj) 的密文
E n c ( H ( k i v i , k j v j ) , k l g ( v i , v j ) ∥ p l g ( v i , v j ) ) Enc(H(k_i^{v_i},k_j^{v_j}),\, k_l^{g(v_i,v_j)} \| p_l^{g(v_i,v_j)}) Enc(H(kivi,kjvj),klg(vi,vj)∥plg(vi,vj))
放在混淆真值表的第 { p i v i , p j v j } \{p_i^{v_i},p_j^{v_j}\} {pivi,pjvj}(或者说 2 p i v i + p j v j 2p_i^{v_i}+p_j^{v_j} 2pivi+pjvj)个位置。
Alice将上述混淆电路发给Bob后,Bob按照拓扑排序进行计算:
- 首先计算电路 G C GC GC的电路输入线,他从Alice那里获取到那些逻辑值 v i v_i vi对应的“标签-选择比特”对 k i v i ∥ p i v i ∈ { 0 , 1 } n + 1 k_i^{v_i} \| p_i^{v_i} \in \{0,1\}^{n+1} kivi∥pivi∈{0,1}n+1,然后通过解密门 g g g的第 2 p i v i + p j v j 2p_i^{v_i}+p_j^{v_j} 2pivi+pjvj个位置的条目,得到门输出线的 k l v l ∥ p l v l ∈ { 0 , 1 } n + 1 k_l^{v_l} \| p_l^{v_l} \in \{0,1\}^{n+1} klvl∥plvl∈{0,1}n+1
- 对于中间的门,我们就获得了其所有的门输入线上的标签和选择比特,继续计算。
- 计算完整个电路后,获得最终结果的标签 k o v ∥ ⊥ k_o^v \| \perp kov∥⊥,然后Alice公布对应关系,结束。
Free XOR
姚的混淆电路在构建的时候,无论是什么 1-out-of-2 逻辑门(与、或、异或、与非、或非)都需要计算 4 4 4个密文。Kolesnikov 等人针对异或门的特殊性质,给出了不必构造混淆真值表的异或门(Free XOR)的构造。同时,非门本身的计算就是“免费的”,交换 label 即可。
对于异或门的观察如下:假设三根线分别为 a , b , c a,b,c a,b,c,随机选择 w a 0 , w b 0 , R ∈ { 0 , 1 } n w_a^0,w_b^0,R \in \{0,1\}^n wa0,wb0,R∈{0,1}n,设置
w c 0 = w a 0 ⊕ w b 0 w_c^0 = w_a^0 \oplus w_b^0 wc0=wa0⊕wb0
以及
∀ i ∈ { a , b , c } , w i 1 = w i 0 ⊕ R \forall i \in \{a,b,c\},\, w_i^1 = w_i^0 \oplus R ∀i∈{a,b,c},wi1=wi0⊕R
那么容易验证上述关系就是 XOR 的逻辑:
w c 0 = w a 0 ⊕ w b 0 = ( w a 0 ⊕ R ) ⊕ ( w b 0 ⊕ R ) = w a 1 ⊕ w b 1 w_c^0 = w_a^0 \oplus w_b^0 = (w_a^0 \oplus R) \oplus (w_b^0 \oplus R) = w_a^1 \oplus w_b^1 wc0=wa0⊕wb0=(wa0⊕R)⊕(wb0⊕R)=wa1⊕wb1
w c 1 = w c 0 ⊕ R = w a 0 ⊕ w b 0 ⊕ R = w a 0 ⊕ ( w b 0 ⊕ R ) = w b 0 ⊕ ( w a 0 ⊕ R ) = w a 0 ⊕ w b 1 = w a 1 ⊕ w b 0 w_c^1 = w_c^0 \oplus R = w_a^0 \oplus w_b^0 \oplus R = w_a^0 \oplus (w_b^0 \oplus R) = w_b^0 \oplus (w_a^0 \oplus R) = w_a^0 \oplus w_b^1 = w_a^1 \oplus w_b^0 wc1=wc0⊕R=wa0⊕wb0⊕R=wa0⊕(wb0⊕R)=wb0⊕(wa0⊕R)=wa0⊕wb1=wa1⊕wb0
由于 R R R是随机数,因此 w i v w_i^v wiv都不会泄露 v v v的信息。在本构造中, R R R是全局的(global)。
混淆电路的构造
令 w = { k , p } ∈ { 0 , 1 } n + 1 w = \{k,p\} \in \{0,1\}^{n+1} w={k,p}∈{0,1}n+1,其中 k k k是线标签, p p p是选择比特。全局的随机数 R ∈ { 0 , 1 } n R \in \{0,1\}^n R∈{0,1}n。随机生成 w i 0 = { k i 0 , p i 0 } w_i^0 = \{k_i^0,p_i^0\} wi0={ki0,pi0},那么
w i 1 = { k i 1 , p i 1 } = { k i 0 ⊕ R , p i 0 ⊕ 1 } w_i^1 = \{k_i^1,\, p_i^1\} = \{k_i^0 \oplus R,\, p_i^0 \oplus 1\} wi1={ki1,pi1}={ki0⊕R,pi0⊕1}
令 H : { 0 , 1 } ∗ → { 0 , 1 } n + 1 H:\{0,1\}^* \to \{0,1\}^{n+1} H:{0,1}∗→{0,1}n+1是 ROM 下的Hash函数。

上图中的第3步中,Alice同时为电路输出线制作了混淆表,它包含两个条目(输出比特是 0 0 0还是 1 1 1)。这样,当Bob计算完电路后,不必再与Alice通信一轮来获得label和value的对应关系,而是直接自己计算出来。节省了一轮通信。
混淆电路的计算
Bob使用不经意传输获得自己的私有输入的标签和选择比特。
安全性
上述 Free XOR 协议是在半诚实敌手的场景下安全的(secure against semi-honest adversaries)。
使用 cut-and-choose method,可以提升为在恶意敌手(malicious adversaries)的场景下安全的。
Garbled Row Reduction
GRR3:1999年 Naor 等人提出了一种可以将混淆表的条目从 4 4 4降低到 3 3 3的方法,同时可以兼容 Free XOR,使得通信量降低了 25 % 25\% 25%。作者还没细看~~
GRR2:2009年 Pinkas 等人提出了一种可以将混淆表的条目从 4 4 4降低到 2 2 2的方法,使得通信量降低了 50 % 50\% 50%。方案是使用拉格朗日插值公式,而非加密算法。
仅考虑 2-to-1 逻辑门(任意 m-to-1 逻辑门可以表示为一组 2-to-1 逻辑门,而 1-to-1 逻辑门可以简化为 1 1 1根导线)。对于真值表包含奇数个“1”的逻辑门,叫它奇逻辑门(odd gate);否则,叫它偶逻辑门(even gate)。
对于逻辑门的 4 4 4个条目,标记为 { 1 , 2 , 3 , 4 } \{1,2,3,4\} {1,2,3,4}。逻辑门 g g g的两根输入线是 i , j i,j i,j,输出线是 l l l,线标记为 k i v i , k j v j , k l v l ∈ { 0 , 1 } n k_i^{v_i},k_j^{v_j},k_l^{v_l} \in \{0,1\}^n kivi,kjvj,klvl∈{0,1}n,对应的选择比特为 p i v i , p j v j , p l v l ∈ { 0 , 1 } p_i^{v_i},p_j^{v_j},p_l^{v_l} \in \{0,1\} pivi,pjvj,plvl∈{0,1}。
构造有限域 G F ( 2 t ) = G F ( 2 ) [ x ] / ( f ( x ) ) GF(2^t) = GF(2)[x]/(f(x)) GF(2t)=GF(2)[x]/(f(x)),以及多项式环 G F ( 2 t ) [ X ] GF(2^t)[X] GF(2t)[X]。
设置条目位置 r = 2 p i v i + p j v j + 1 r = 2p_i^{v_i}+p_j^{v_j}+1 r=2pivi+pjvj+1,计算条目的掩码(the value used to mask this entry):
K r ∥ M r = K D F t + 1 ( k i v i , k j v j , s ) K_r \| M_r = KDF^{t+1}(k_i^{v_i},k_j^{v_j},s) Kr∥Mr=KDFt+1(kivi,kjvj,s)
其中 s = G i d ∥ p i v i ∥ p j v j s = Gid \| p_i^{v_i} \| p_j^{v_j} s=Gid∥pivi∥pjvj, K r ∈ { 0 , 1 } t K_r \in \{0,1\}^t Kr∈{0,1}t是有限域元素, M r ∈ { 0 , 1 } M_r \in \{0,1\} Mr∈{0,1}用来加密门输出线的选择比特 p l v l p_l^{v_l} plvl
odd gate
对于奇数门,在真值表上要么有 3 3 3个“1”,要么有 3 3 3个“0”。以 OR 门举例:它有 3 3 3个“1”,分别位于条目的第 2 , 3 , 4 2,3,4 2,3,4位置。
| OR Gate | v i v_i vi | v j v_j vj | v l v_l vl |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 |
| 4 | 1 | 1 | 1 |
Alice按照拓扑排序,生成逻辑门的线标签和选择比特,根据两根输入线的 4 4 4个 k ∥ p k\|p k∥p,用 K D F KDF KDF计算出 4 4 4个位置的掩码 K r ∥ M r K_r \| M_r Kr∥Mr
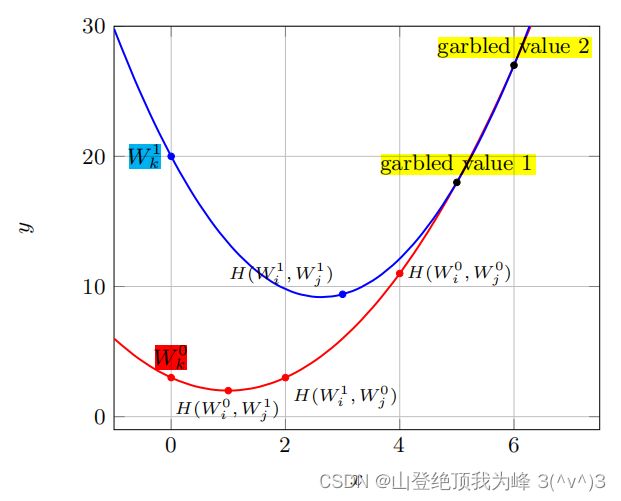
我们定义二次多项式 P ( X ) ∈ G F ( 2 t ) [ X ] P(X) \in GF(2^t)[X] P(X)∈GF(2t)[X],它经过三个点: ( 2 , K 2 ) , ( 3 , K 3 ) , ( 4 , K 4 ) (2,K_2),\, (3,K_3),\, (4,K_4) (2,K2),(3,K3),(4,K4),可以用拉格朗日插值法计算出 P ( X ) P(X) P(X)
然后计算额外的两点 ( 5 , K 5 ) , ( 6 , K 6 ) (5,K_5),\, (6,K_6) (5,K5),(6,K6),它们连同 ( 1 , K 1 ) (1,K_1) (1,K1)一同做拉格朗日插值,计算出另一个二次多项式 Q ( X ) ∈ G F ( 2 t ) [ X ] Q(X) \in GF(2^t)[X] Q(X)∈GF(2t)[X]
定义输出线的标签为两个函数的 y − y- y−截矩:
k l 0 = P ( 0 ) , k l 1 = Q ( 0 ) k_l^0 = P(0),\, k_l^1 = Q(0) kl0=P(0),kl1=Q(0)
注意,这里的 0 , 1 , 2 , 3 , 4 , 5 , 6 ∈ G F ( 2 t ) 0,1,2,3,4,5,6 \in GF(2^t) 0,1,2,3,4,5,6∈GF(2t)都是有限域元素,例如 2 : = x + 1 2 := x+1 2:=x+1
另外,输出线的选择比特 p l v l p_l^{v_l} plvl也应当被保护起来。使用 M r M_r Mr来加密:
e r = p l v l ⊕ M r , r = 1 , 2 , 3 , 4 e_r = p_l^{v_l} \oplus M_r,\, r=1,2,3,4 er=plvl⊕Mr,r=1,2,3,4
Alice在发送混淆电路时,每一个奇逻辑门需要发送 K 5 , K 6 K_5,K_6 K5,K6以及 e r , r = 1 , 2 , 3 , 4 e_r,r=1,2,3,4 er,r=1,2,3,4,一共是 2 t + 4 2t+4 2t+4比特。
| 公共点1 | 公共点2 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| K 5 K_5 K5 | K 6 K_6 K6 | e 1 e_1 e1 | e 2 e_2 e2 | e 3 e_3 e3 | e 4 e_4 e4 |
Bob接收到 odd gate 的混淆表:
- 根据已知的输入线的 k i v i ∥ p i v i , k j v j ∥ p j v j k_i^{v_i}\|p_i^{v_i},k_j^{v_j}\|p_j^{v_j} kivi∥pivi,kjvj∥pjvj,用 K D F KDF KDF计算出原始真值表的其中一个条目的掩码 K r ∥ M r K_r\|M_r Kr∥Mr,条目的位置是 r = 2 p i v i + p j v j + 1 r=2p_i^{v_i}+p_j^{v_j}+1 r=2pivi+pjvj+1。
- 然后根据 ( r , K r ) , ( 5 , K 5 ) , ( 6 , K 6 ) (r,K_r),(5,K_5),(6,K_6) (r,Kr),(5,K5),(6,K6)插值得到多项式 R ( X ) R(X) R(X),它可能是 P ( X ) P(X) P(X)也可能是 Q ( X ) Q(X) Q(X),这取决于 v l v_l vl的值。
- 计算 k l v l = R ( 0 ) k_l^{v_l} = R(0) klvl=R(0),解密 p l v l = e r ⊕ M r p_l^{v_l} = e_r \oplus M_r plvl=er⊕Mr,得到门输出线的 k l v l ∥ p l v l k_l^{v_l}\|p_l^{v_l} klvl∥plvl,进行后续逻辑门的计算。
在 Yakoubov 的综述中,给出了一个描绘 odd gate 原理的图:
even gate
而非平凡的 2-to-1 偶数门只有异或门(XOR)和同或门(NXOR),其他的偶数门都可以化简成一根电线(全0,全1,传递其中1根线的值)。这两个门都有 2 2 2个“0”和 2 2 2个“1”。
以 XOR 门举例:它有 2 2 2个“1”,分别位于条目的第 2 , 3 2,3 2,3位置;第 1 , 4 1,4 1,4位置都是 0 0 0
| XOR Gate | v i v_i vi | v j v_j vj | v l v_l vl |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 |
| 4 | 1 | 1 | 0 |
Alice按照拓扑排序,生成逻辑门的线标签和选择比特,根据两根输入线的 4 4 4个 k ∥ p k\|p k∥p,用 K D F KDF KDF计算出 4 4 4个位置的掩码 K r ∥ M r K_r \| M_r Kr∥Mr
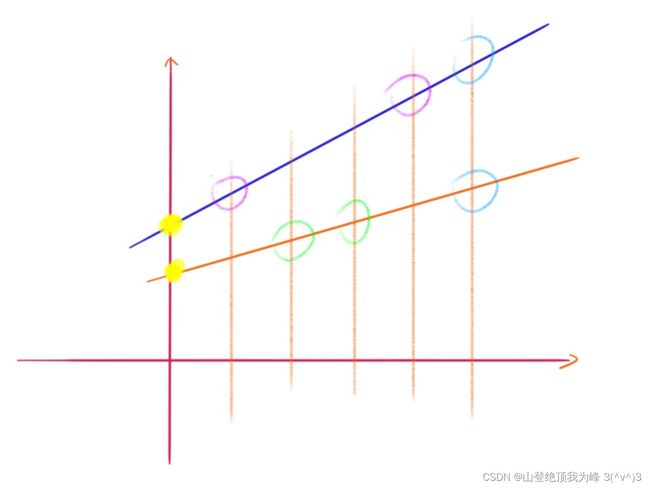
我们定义线性多项式 P ( X ) ∈ G F ( 2 t ) [ X ] P(X) \in GF(2^t)[X] P(X)∈GF(2t)[X],对应输出 0 0 0,它经过两个点: ( 1 , K 1 ) , ( 4 , K 4 ) (1,K_1),\,(4,K_4) (1,K1),(4,K4),使用拉格朗日插值法(两点式)得到。然后计算 K 5 = P ( 5 ) K_5 = P(5) K5=P(5),如果输出线的选择比特 p l 0 = 0 p_l^0=0 pl0=0,那么存放在混淆表的第一个条目上,否则放在第二个条目上。
同时定义线性多项式 Q ( X ) ∈ G F ( 2 t ) [ X ] Q(X) \in GF(2^t)[X] Q(X)∈GF(2t)[X],对应输出 1 1 1,它经过两个点: ( 2 , K 2 ) , ( 3 , K 3 ) (2,K_2),\,(3,K_3) (2,K2),(3,K3),使用拉格朗日插值法(两点式)得到。然后计算 K 5 ′ = Q ( 5 ) K_5' = Q(5) K5′=Q(5),如果输出线的选择比特 p l 1 = 1 p_l^1=1 pl1=1,那么存放在混淆表的第二个条目上,否则放在第一个条目上。
注意,上述使用的选择比特是输出线的!并非输入线的选择比特。因为 P ( x ) P(x) P(x)对应的是 v l = 0 v_l=0 vl=0, Q ( x ) Q(x) Q(x)对应的是 v l = 1 v_l=1 vl=1,那么 P ( 0 ) , Q ( 0 ) P(0),Q(0) P(0),Q(0)也分别对应两者。
定义输出线的标签为两个函数的 y − y- y−截矩:
k l 0 = P ( 0 ) , k l 1 = Q ( 0 ) k_l^0 = P(0),\, k_l^1 = Q(0) kl0=P(0),kl1=Q(0)
另外,输出线的选择比特 p l v l p_l^{v_l} plvl分别使用 M r M_r Mr来加密,密文是 e r , r = 1 , 2 , 3 , 4 e_r,r=1,2,3,4 er,r=1,2,3,4。计算电路时,为了确定使用混淆表的哪个条目,需要先解密!
Alice在发送混淆电路时,每一个偶逻辑门需要发送 K 5 , K 5 ′ K_5,K_5' K5,K5′以及 e r , r = 1 , 2 , 3 , 4 e_r,r=1,2,3,4 er,r=1,2,3,4,一共是 2 t + 4 2t+4 2t+4比特。对于 p l 0 = 0 , p l 1 = 1 p_l^0=0,p_l^1=1 pl0=0,pl1=1的情况,混淆表如下:
| P P P的辅助点 | Q Q Q的辅助点 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| K 5 K_5 K5 | K 5 ′ K_5' K5′ | e 1 e_1 e1 | e 2 e_2 e2 | e 3 e_3 e3 | e 4 e_4 e4 |
Bob接收到 even gate 的混淆表:
- 根据已知的输入线的 k i v i ∥ p i v i , k j v j ∥ p j v j k_i^{v_i}\|p_i^{v_i},k_j^{v_j}\|p_j^{v_j} kivi∥pivi,kjvj∥pjvj,用 K D F KDF KDF计算出原始真值表的其中一个条目的掩码 K r ∥ M r K_r\|M_r Kr∥Mr,条目的位置是 r = 2 p i v i + p j v j + 1 r=2p_i^{v_i}+p_j^{v_j}+1 r=2pivi+pjvj+1。
- 然后用 M r M_r Mr解密出 p l v l = e r ⊕ M r p_l^{v_l} = e_r \oplus M_r plvl=er⊕Mr,
- 如果 p l v l = 0 p_l^{v_l}=0 plvl=0,那么根据 ( r , K r ) (r,K_r) (r,Kr)和第一个条目 ( 5 , K 5 ) (5,K_5) (5,K5)插值得到多项式 P ( X ) P(X) P(X),计算出 k l 0 = P ( 0 ) k_l^0 = P(0) kl0=P(0),Bob得到了门输出线的 k l 0 ∥ p l 0 k_l^0\|p_l^0 kl0∥pl0
- 如果 p l v l = 1 p_l^{v_l}=1 plvl=1,那么根据 ( r , K r ) (r,K_r) (r,Kr)和第二个条目 ( 5 , K 5 ′ ) (5,K_5') (5,K5′)插值得到多项式 Q ( X ) Q(X) Q(X),计算出 k l 1 = Q ( 0 ) k_l^1 = Q(0) kl1=Q(0),Bob得到了门输出线的 k l 1 ∥ p l 1 k_l^1\|p_l^1 kl1∥pl1
- Bob继续进行后续逻辑门的计算。
对于 p l 0 = 1 , p l 1 = 0 p_l^0=1,p_l^1=0 pl0=1,pl1=0的情况,过程类似,
- 如果 p l v l = 0 p_l^{v_l}=0 plvl=0,那么根据 ( r , K r ) (r,K_r) (r,Kr)和第一个条目 ( 5 , K 5 ′ ) (5,K_5') (5,K5′)插值得到多项式 Q ( X ) Q(X) Q(X),计算出 k l 1 = Q ( 0 ) k_l^1 = Q(0) kl1=Q(0),Bob得到了门输出线的 k l 1 ∥ p l 1 k_l^1\|p_l^1 kl1∥pl1
- 如果 p l v l = 1 p_l^{v_l}=1 plvl=1,那么根据 ( r , K r ) (r,K_r) (r,Kr)和第二个条目 ( 5 , K 5 ) (5,K_5) (5,K5)插值得到多项式 P ( X ) P(X) P(X),计算出 k l 0 = P ( 0 ) k_l^0 = P(0) kl0=P(0),Bob得到了门输出线的 k l 0 ∥ p l 0 k_l^0\|p_l^0 kl0∥pl0
由于 p l v l p_l^{v_l} plvl并不透露 v l v_l vl的信息,因此Bob实际上无法区分上述两种情况。Bob只根据 p l v l p_l^{v_l} plvl来挑选使用第几个条目,然后计算出的 label k l v l k_l^{v_l} klvl就是 XOR Gate 的正确输出 v l v_l vl所对应的。
两类门的连接
Alice在生成混淆电路时,无论哪种逻辑门,她都是知道输出线的逻辑值和标签与选择比特的关系的。因此Alice可以根据电路 C C C生成混淆电路 G C GC GC。
另外,Bob也是知道 C C C的构造,因此他知道哪些门是 odd gate,哪些门是 even gate,从而正确地计算电路。