LeNet复现pytorch --简单神经网络的搭建与训练

LeNet网络简介：
首先介绍一下LeNet, 定义了CNN的基本组件，是CNN的鼻祖。
LeNet由七层CNN组成，
C1卷积层:使用6个5*5的卷积核，得到6个feature map。输入图像为32*32，因此特征图大小为28*28。
参数个数：对于同个卷积核每个神经元使用的参数相同。因此参数个数是（5*5+1）*6=156，其中，5*5为卷积核参数，1为偏置参数。
连接数：每个特征图28*28个神经元，因此连接数为二者乘积：（5*5+1）*6*28*28=122304

S2下采样层：池化单元2*2，因此特征图的大小变成14*14。
计算过程是，2*2个单元里的值相加，乘以训练参数w,加上偏置参数，然后取sigmoid值，作为相应单位的值。
参数个数：每个特征图都共享w和b这两个参数，需要2*6=12个参数。
连接数：每个池化单元连接数为2*2+1，因此连接数为（2*2+1）*14*14*6。

C3卷积层：输入为6个14*14的特征图，经过16个5*5的卷积核 输出16个10*10 的特征图。
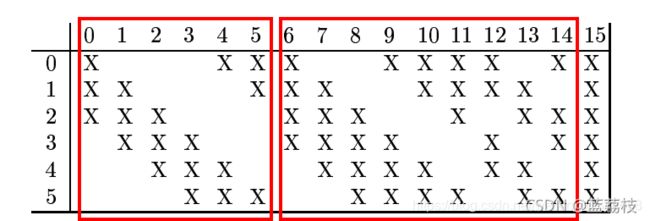
16个特征平面是如何和上一层池化层对应的？每个特征平面对应的卷积核和池化层的多个平面进行卷积。把C3的卷积平面编号即0,1,2，......15，池化层S2编号为0,1，......5,对应关系如下图：

可以观察到前六个平面是对应池化层的三个平面，6—14对应池化层的四个平面。
因此连接数：
（5*5*3+1）*10*10*6+（5*5*4+1）*10*10*9+（5*5*6+1）*10*10=151600
参数个数： (5x5x3+1)x6 + (5x5x4+1)x9 + 5x5x6+1  = 456 + 909+151 = 1516
这么做的目的是打破对称性，提取深层特征。

S4池化层：池化单元2*2，得到16个5*5的特征图
连接数：（2*2+1）*5*5*16
可训练参数：2*16=32（和的权+偏置）

C5卷积层：输入为16个5*5的特征图，经过 120个5*5的卷积核，输出120个1*1的特征图
因为S4输出的特征图大小为5*5所以，第五层可以看成全连接层，输出120个1*1的特征图
每个卷积核只对应一个神经元了，因此本层只有120个神经元并列排列，每个神经元连接池化层的所有层。 C5层的每个神经元的连接数为5x5x16+1
连接数=参数：（16*5*5+1）*120

F6全连接层：84个神经元，每一个神经元都和C5的120个神经元全连接，连接数为（120+1）*84
Output全连接层：
一共10个节点，分别代表数字0~9。

pytorch 复现代码：
搭建模型：model.py

from torch.nn import Module
from torch import nn
 
 
class Model(Module):
    def __init__(self):
        super(Model, self).__init__()
        # 卷积层C1 通道数为1 6个大小为5*5的卷积核
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.relu1 = nn.ReLU()
        # 下采样层 size为2*2，步长为1的池化层
        self.pool1 = nn.MaxPool2d(2)
        # 卷积层
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.relu2 = nn.ReLU()
        # 池化层
        self.pool2 = nn.MaxPool2d(2)
        # 全连接层
        self.fc1 = nn.Linear(256, 120)
        self.relu3 = nn.ReLU()
        # 全连接层
        self.fc2 = nn.Linear(120, 84)
        self.relu4 = nn.ReLU()
        # 输出层
        self.fc3 = nn.Linear(84, 10)
        self.relu5 = nn.ReLU()
 
    # 搭建网络结构
    def forward(self, x):
        y = self.conv1(x)
        y = self.relu1(y)
        y = self.pool1(y)
        y = self.conv2(y)
        y = self.relu2(y)
        y = self.pool2(y)
        # y.size(0)指batchsize的值
        # view函数用来改变tensor的形状的
        # 在CNN卷积或者池化之后需要连接全连接层，需要把多维度的tensor展平称一维
        # -1表示会自适应的调整剩余的维度
        y = y.view(y.shape[0], -1)
        y = self.fc1(y)
        y = self.relu3(y)
        y = self.fc2(y)
        y = self.relu4(y)
        y = self.fc3(y)
        y = self.relu5(y)
        return y
 
 
# model = Model()
# print(model)
 
# Model(
#   (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
#   (relu1): ReLU()
#   (pool1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
#   (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
#   (relu2): ReLU()
#   (pool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
#   (fc1): Linear(in_features=256, out_features=120, bias=True)
#   (relu3): ReLU()
#   (fc2): Linear(in_features=120, out_features=84, bias=True)
#   (relu4): ReLU()
#   (fc3): Linear(in_features=84, out_features=10, bias=True)
#   (relu5): ReLU()
# )
 
 

训练：train.py

from model import Model
import numpy as np
 
import torch
from torchvision.datasets import mnist
from torch.nn import CrossEntropyLoss
# 包含优化算法的包
from torch.optim import SGD
# 可迭代的数据集
from torch.utils.data import DataLoader
from torchvision.transforms import ToTensor
 
if __name__ == '__main__':
    batch_size = 256
    # 定义数据集
    train_dataset = mnist.MNIST(root='./train', train=True, transform=ToTensor())
    test_dataset = mnist.MNIST(root='./test', train=False, transform=ToTensor())
    # load数据集
    train_loader = DataLoader(train_dataset, batch_size=batch_size)
    test_loader = DataLoader(test_dataset, batch_size=batch_size)
    # 定义模型
    model = Model()
    # 优化方法
    sgd = SGD(model.parameters(), lr=1e-1)from model import Model
import numpy as np
 
import torch
from torchvision.datasets import mnist
from torch.nn import CrossEntropyLoss
# 包含优化算法的包
from torch.optim import SGD
# 可迭代的数据集
from torch.utils.data import DataLoader
from torchvision.transforms import ToTensor
 
if __name__ == '__main__':
    batch_size = 256
    # 定义数据集
    train_dataset = mnist.MNIST(root='./train', train=True, transform=ToTensor())
    test_dataset = mnist.MNIST(root='./test', train=False, transform=ToTensor())
    # load数据集
    train_loader = DataLoader(train_dataset, batch_size=batch_size)
    test_loader = DataLoader(test_dataset, batch_size=batch_size)
    # 定义模型
    model = Model()
    # 优化方法
    sgd = SGD(model.parameters(), lr=1e-1)
    # 交叉熵损失函数
    cost = CrossEntropyLoss()
    # 迭代次数
    epoch = 40
 
    # 开始迭代
    for _epoch in range(epoch):
        for idx, (train_x, train_label) in enumerate(train_loader):
            # 返回一个给定形状和类型的用0填充的数组
            label_np = np.zeros((train_label.shape[0], 10))
            # 将模型中参数的梯度置为0
            sgd.zero_grad()
            # 预测的y值
            predict_y = model(train_x.float())
            # 计算误差
            loss = cost(predict_y, train_label.long())
            if idx % 10 == 0:
                print('idx: {}, loss: {}'.format(idx, loss.sum().item()))
            # pytorch里反向传播里基于一个loss标量 从中获取grad
            loss.backward()
            sgd.step()
 
        # 预测正确的数目
        correct = 0
        # 总数
        _sum = 0
 
        # 计算准确率
        for idx, (test_x, test_label) in enumerate(test_loader):
            predict_y = model(test_x.float()).detach()
            predict_ys = np.argmax(predict_y, axis=-1)
            label_np = test_label.numpy()
 
            _ = predict_ys == test_label
            correct += np.sum(_.numpy(), axis=-1)
            _sum += _.shape[0]
 
        # 输出精度
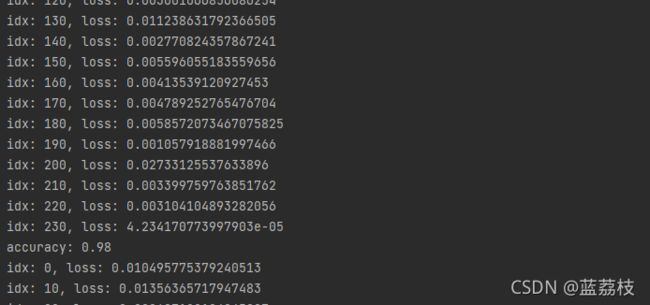
        print('accuracy: {:.2f}'.format(correct / _sum))
        # 保存模型
        torch.save(model, 'models/mnist_{:.2f}.pkl'.format(correct / _sum))
 
    # 交叉熵损失函数
    cost = CrossEntropyLoss()
    # 迭代次数
    epoch = 40
 
    # 开始迭代
    for _epoch in range(epoch):
        for idx, (train_x, train_label) in enumerate(train_loader):
            label_np = np.zeros((train_label.shape[0], 10))
            # 将模型中参数的梯度置为0
            sgd.zero_grad()
            # 预测的y值
            predict_y = model(train_x.float())
            # 计算误差
            loss = cost(predict_y, train_label.long())
            if idx % 10 == 0:
                print('idx: {}, loss: {}'.format(idx, loss.sum().item()))
            # pytorch里反向传播里基于一个loss标量 从中获取grad
            loss.backward()
            sgd.step()
 
        correct = 0
        _sum = 0
 
        # 计算准确率
        for idx, (test_x, test_label) in enumerate(test_loader):
            predict_y = model(test_x.float()).detach()
            predict_ys = np.argmax(predict_y, axis=-1)
            label_np = test_label.numpy()
            _ = predict_ys == test_label
            correct += np.sum(_.numpy(), axis=-1)
            _sum += _.shape[0]
 
        # 输出准确率
        print('accuracy: {:.2f}'.format(correct / _sum))
        # 保存模型
        torch.save(model, 'models/mnist_{:.2f}.pkl'.format(correct / _sum))

训练结果：