TSA优化算法——模仿航海过程中外套的喷气推进和蜂群行为（Matlab代码实现）

 欢迎来到本博客❤️❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者，博主专门做了一个专栏目录，整个专栏只放了一篇文章，足见我对其重视程度：博主专栏目录。做到极度细致，方便大家进行学习！亲民！！！还有我开了一个专栏给女朋友的，很浪漫的喔，代码学累的时候去瞧一瞧，看一看：女朋友的浪漫邂逅。有问题可以私密博主，博主看到会在第一时间回复。
目前更新：期刊论文，算法，机器学习和人工智能学习。
支持：如果觉得博主的文章还不错或者您用得到的话，可以关注一下博主，如果三连收藏支持就更好啦！这就是给予我最大的支持！

                          

                                    欢迎您的到来

                     ⛅⛅⛅ 个人主页：科研室

                    所有代码目录：电气工程科研社‍‍‍

                           

【现在公众号名字改为：荔枝科研社】

本文目录如下：⛳️⛳️⛳️

​

目录

1 概述

2 数学模型 

3 运行结果

4 Matlab代码及文章详细讲解

5 参考文献

6 写在最后

1 概述

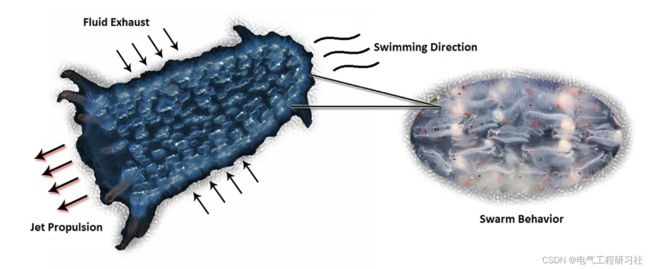
本文介绍了一种名为 Tunicate Swarm 算法 (TSA) 的仿生元启发式优化算法。所提出的算法在导航和觅食过程中模仿被囊动物的喷气推进和集群行为。使用敏感性、收敛性和可扩展性分析以及 ANOVA 测试对 74 个基准测试问题评估 TSA 的性能。该算法的功效进一步与基于生成的最优解的几种广受好评的元启发式方法进行比较。此外，我们还在六个约束和一个无约束的工程设计问题上执行了所提出的算法，以进一步验证其鲁棒性。仿真结果表明，与其他竞争算法相比，TSA 生成了更好的最优解，并且能够解决具有未知搜索空间的真实案例研究。

2 数学模型 

Tunicate 有能力在海洋中找到食物来源的位置。但是，对于给定搜索空间中的食物来源一无所知。本文采用被囊动物的两种行为来寻找食物来源，即最优。这些行为是喷气推进和群体智能。为了对喷气推进行为进行数学建模，被囊动物应满足三个条件，即避免搜索代理之间的冲突、向最佳搜索代理的位置移动以及与最佳搜索代理保持接近。然而，群体行为将更新其他搜索代理的位置以获得最佳最优解。这些行为的数学建模在前面的小节中进行了描述：

                           

                      

                    

             

详细数学模型见第4部分。

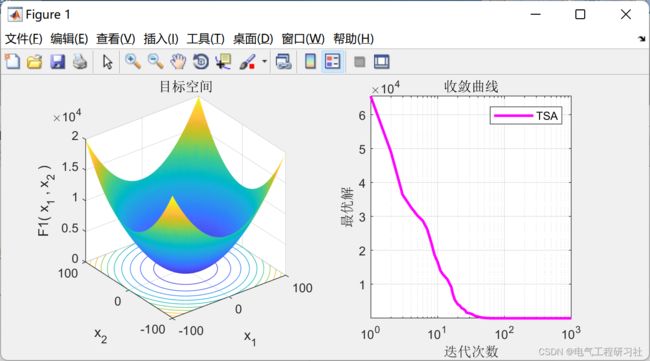
3 运行结果

 

  

4 Matlab代码及文章详细讲解

 本文仅展现部分代码，全部代码及文献详细阅读见：正在为您运送作品详情

clear all 
clc
SearchAgents=30; 
Fun_name='F1';    %换成自己需要的目标函数，可以F2、F3.....
Max_iterations=1000; 
[lowerbound,upperbound,dimension,fitness]=fun_info(Fun_name);
[Best_score,Best_pos,TSA_curve]=tsa(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness);


figure('Position',[500 500 660 290])

subplot(1,2,1);
func_plot(Fun_name);
title('目标空间')
xlabel('x_1');
ylabel('x_2');
zlabel([Fun_name,'( x_1 , x_2 )'])

subplot(1,2,2);
plots=semilogx(TSA_curve,'Color','m');
set(plots,'linewidth',2)
hold on
title('收敛曲线')
xlabel('迭代次数');
ylabel('最优解');

axis tight
grid on
box on
legend('TSA')

display(['TSA得到的最优解是 : ', num2str(Best_pos)]);
display(['TSA找到的目标函数的最优值是 : ', num2str(Best_score)]);

        

function [lowerbound,upperbound,dimension,fitness] = fun_info(F)


switch F
    case 'F1'
        fitness = @F1;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F2'
        fitness = @F2;
        lowerbound=-10;
        upperbound=10;
        dimension=30;
        
    case 'F3'
        fitness = @F3;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F4'
        fitness = @F4;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F5'
        fitness = @F5;
        lowerbound=-30;
        upperbound=30;
        dimension=30;
        
    case 'F6'
        fitness = @F6;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F7'
        fitness = @F7;
        lowerbound=-1.28;
        upperbound=1.28;
        dimension=30;
        
    case 'F8'
        fitness = @F8;
        lowerbound=-500;
        upperbound=500;
        dimension=30;
        
    case 'F9'
        fitness = @F9;
        lowerbound=-5.12;
        upperbound=5.12;
        dimension=30;
        
    case 'F10'
        fitness = @F10;
        lowerbound=-32;
        upperbound=32;
        dimension=30;
        
    case 'F11'
        fitness = @F11;
        lowerbound=-600;
        upperbound=600;
        dimension=30;
        
    case 'F12'
        fitness = @F12;
        lowerbound=-50;
        upperbound=50;
        dimension=30;
        
    case 'F13'
        fitness = @F13;
        lowerbound=-50;
        upperbound=50;
        dimension=30;
        
    case 'F14'
        fitness = @F14;
        lowerbound=-65.536;
        upperbound=65.536;
        dimension=2;
        
    case 'F15'
        fitness = @F15;
        lowerbound=-5;
        upperbound=5;
        dimension=4;
        
    case 'F16'
        fitness = @F16;
        lowerbound=-5;
        upperbound=5;
        dimension=2;
        
    case 'F17'
        fitness = @F17;
        lowerbound=[-5,0];
        upperbound=[10,15];
        dimension=2;
        
    case 'F18'
        fitness = @F18;
        lowerbound=-2;
        upperbound=2;
        dimension=2;
        
    case 'F19'
        fitness = @F19;
        lowerbound=0;
        upperbound=1;
        dimension=3;
        
    case 'F20'
        fitness = @F20;
        lowerbound=0;
        upperbound=1;
        dimension=6;     
        
    case 'F21'
        fitness = @F21;
        lowerbound=0;
        upperbound=10;
        dimension=4;    
        
    case 'F22'
        fitness = @F22;
        lowerbound=0;
        upperbound=10;
        dimension=4;    
        
    case 'F23'
        fitness = @F23;
        lowerbound=0;
        upperbound=10;
        dimension=4;            
end

end

% F1

function R = F1(x)
R=sum(x.^2);
end

% F2

function R = F2(x)
R=sum(abs(x))+prod(abs(x));
end

% F3

function R = F3(x)
dimension=size(x,2);
R=0;
for i=1:dimension
    R=R+sum(x(1:i))^2;
end
end

% F4

function R = F4(x)
R=max(abs(x));
end

% F5

function R = F5(x)
dimension=size(x,2);
R=sum(100*(x(2:dimension)-(x(1:dimension-1).^2)).^2+(x(1:dimension-1)-1).^2);
end

% F6

function R = F6(x)
R=sum(abs((x+.5)).^2);
end

% F7

function R = F7(x)
dimension=size(x,2);
R=sum([1:dimension].*(x.^4))+rand;
end

% F8

function R = F8(x)
R=sum(-x.*sin(sqrt(abs(x))));
end

% F9

function R = F9(x)
dimension=size(x,2);
R=sum(x.^2-10*cos(2*pi.*x))+10*dimension;
end

% F10

function R = F10(x)
dimension=size(x,2);
R=-20*exp(-.2*sqrt(sum(x.^2)/dimension))-exp(sum(cos(2*pi.*x))/dimension)+20+exp(1);
end

% F11

function R = F11(x)
dimension=size(x,2);
R=sum(x.^2)/4000-prod(cos(x./sqrt([1:dimension])))+1;
end

% F12

function R = F12(x)
dimension=size(x,2);
R=(pi/dimension)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dimension-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dimension)+1)./4)))).^2))+((x(dimension)+1)/4)^2)+sum(Ufun(x,10,100,4));
end

% F13

function R = F13(x)
dimension=size(x,2);
R=.1*((sin(3*pi*x(1)))^2+sum((x(1:dimension-1)-1).^2.*(1+(sin(3.*pi.*x(2:dimension))).^2))+...
((x(dimension)-1)^2)*(1+(sin(2*pi*x(dimension)))^2))+sum(Ufun(x,5,100,4));
end

% F14

function R = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];

for j=1:25
    bS(j)=sum((x'-aS(:,j)).^6);
end
R=(1/500+sum(1./([1:25]+bS))).^(-1);
end

% F15

function R = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
R=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end

% F16

function R = F16(x)
R=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end

% F17

function R = F17(x)
R=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end

% F18

function R = F18(x)
R=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
    (30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));
end

% F19

function R = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
R=0;
for i=1:4
    R=R-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end

% F20

function R = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
R=0;
for i=1:4
    R=R-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end

% F21

function R = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];

R=0;
for i=1:5
    R=R-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end

% F22

function R = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];

R=0;
for i=1:7
    R=R-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end

% F23

function R = F23(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];

R=0;
for i=1:10
    R=R-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end

function R=Ufun(x,a,k,m)
R=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
end

5 参考文献

Mirjalili, S., Mirjalili, S.M., Hatamlou, A., 2016. Multi-verse optimizer: A nature-inspired
algorithm for global optimization. Neural Comput. Appl. 27 (2), 495–513, [On

6 写在最后

部分理论引用网络文献，若有侵权请联系博主删除。