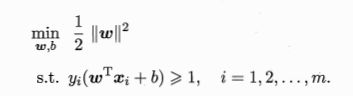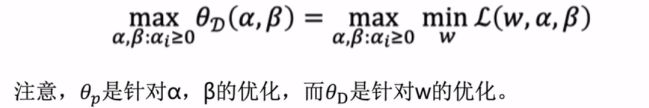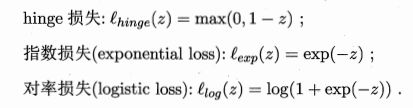每日算法：SVM支持向量机

争取每天搞懂一个算法。                                                                                  --------------wudibooo

目录

0.  最优化问题

0.1 简介

0.2 拉格朗日乘数法

0.3  对偶问题

1.  SVM-支持向量机

1.1  什么是支持向量

1.2 求解SVM

1.3 软间隔（soft margin）

2 核函数

3 多分类问题 

3.1 OVR （one versus rest）

3.1 OVO （one vs one）

 4  pytorch实战

---

0.  最优化问题

0.1 简介

         对于一个求极值的问题，如求f（x）的最小值解，可以分为3种情况：

1.无约束条件

2.等式约束条件，如h(x) = 0

3.不等式约束条件,g(x) < = 0 

---

0.2 拉格朗日乘数法

前提：函数都是凸函数

        无约束条件就正常求导，求解就行。

         在有等式约束条件的时候，求目标函数f(x)的最优解，极值点时，通常情况下要把函数  f(x)  转为无约束条件，我们可以通过把约束条件乘上一个拉格朗日系数  λ ，与原式相加构造一个新的函数  L(x,λ)   ，就可以视为求无约束条件的函数。

        在有不等式约束条件的时候，构造函数时，就需要满足一个条件---KKT，总的来看如下图

KKT条件

        对该式子先最大化再最小化，且满足KKT条件，就和解决原优化问题是等价的。

式  0-1

 为什么等价？

        因为有KTT条件的约束，在可行解区域内，h(x)= 0（约束条件） ,第一个部分就恒等于0, 第二部分的g<0，所以一直是个负数，两者加起来的max值，也不会大于0，所有 f（x）加一个不大于零的数，不会增加，在不可行解得区域，求得是无穷，也就是无解。

        总结而言，两者是相等的。

对于SVM的求解的问题，就是我们提到最优化问题：（SVM最基本的形式）

---

0.3  对偶问题

定义：

         则求该式的最小值与原问题有同样的解：

         那么上式的对偶问题，我们可以定义为

        上面的θD = min L(w ,a ,b) ， θp = max L(w ,a ,b)，两者满足以下式子

         得到θD <= θp 恒成立，且只有在满足KKT时，两者才相等，这时我们通过求解对偶问题来求解原问题。

---

1.  SVM-支持向量机

1.1  什么是支持向量

首先要了解两个东西：间隔和支持向量。

存在多个划分超平面，将两者分开

        对于一个给定的数据集(xi,yi)，我们想将两者分类，基本想法是基于训练集在样本空间上找到一个超平面来对两者进行分类，如图，可以使用的平面有很多，但是我们希望找到鲁棒性最好的（中间那个平面），如何确定呢？

        我们知道超平面的可以表示为：（可以这样理解，3维空间中的点法式，W表示法向量）

式  1

         我们样本点到平面的距离就是：

式 2 

        要让超平面可以正确分类，即假设yi = +1时，要求wTx + b >0， yi = -1时，要求wTx + b<0,才能将两者分开。

        如下图：

        我们要找的超平面就要满足以下条件：

式 3

        距离超平面最近的训练样本点，使得式3成立，我们称他们为支持向量，两个异类支持向量到超平面的距离之和称之为间隔：

式 4

         SVM要找的就是的最大间隔 max  γ，SVM的优化问题可以写为：（为什么是min，因为是倒数）

1.2 求解SVM

        求解SVM的方法，就是上面第0部分里面提出的最优化问题求解得方法，因此我们可以得到该问题的拉格朗日函数：

        对w和b求偏导：

         代入原式，消去其中的w和b，再考虑约束条件，得到SVM原问题的对偶问题：

         通过解出a就可以求出w和x，（如何求出a，再西瓜书P124里有解释说，这是一个二次规划问题，有比较著名的方法是SMO：先选择ai 和 aj固定其余的参数，得到一个aiyi+ajyj = C的等式，然后用aj代入式中，就可以求出ai，具体操作不是很清楚，或者可以去看看这个视频https://www.bilibili.com/video/BV1ZE411p73x?p=5&spm_id_from=pageDriver）

        其中w为：

         现在求b，因为任何支持向量（Xs，Ys）都满足   Ys * F（ Xs ） = 1，s为支持向量的下标集，为求得一个比较中肯的b，我们使用平均值来求：

        可以看到结果，都只和支持向量有关， 支持向量机名字也是这么来的。

1.3 软间隔（soft margin）

        硬间隔表示所有样本必须正确分类，但不是所有的数据集都是完全分开的，那上面提到的支持向量机就没办法工作了，我们只能运行某些样本不用满足约束：

        在此情况下，我们要求不满足约束的样本尽量最少，因此优化的目标就变为

式 1.3.1

         其中L 0 /1是 0 1 损失函数，f（x）- 1  小于0时（不满足约束条件） ，loss = 1，其他为0，C是一个大于0的常数，C无穷大的话，图中的宽度会无限大，所有样本都会满足约束，C为有限值时，就是一个有限的宽度，宽度内的样本允许不满住约束。

        01损失函数的数学性质不太好，通常会用其他的代替。

         引入松弛变量，将式 1. 3 .1重写：

         这就是常见的软间隔支持向量机，如何求解就看西瓜书吧 P130.

2 核函数

        对于线性不可分的问题，我们引入核函数来提升维度，如果原始的维度是有限的，那么一定可以存在一个高维特征空间使样本可分。

        设φ（x）是x映射后的特征向量，那么模型就变为

        对偶问题为：

         在令

         这里的k（ · ）就是我们说的核函数。

        核函数的性质，有哪些原理，我都不太懂，西瓜书讲的也看不明白，有余力的来客可以自行补充。

3 多分类问题 

        SVM一般是用来解决二分类问题的，那么多分类问题怎么解决？ 多用几个SVM呗。

3.1 OVR （one versus rest）

        对于一个K类别的情况，我们要训练K个SVM，第j个SVM判别器使用来判别样本点事属于j类还是不属于j类。最后在预测时，具有最大值的wT（i）x + b（i）表示给定的数据x属于类别i。

        比如 ，在下图的分类问题，要训练3个SVM，分别用来分类A 非A,B非 B，C 非C，预测时，将要预测的样本点代入每个SVM中计算wTx+b，如果求得在A的SVM最大，那么就预测为A。

3.1 OVO （one vs one）

        同样是一个K类问题，但是这种方法要用K * （K-1）/2个SVM，就很多，预测的时候，代入每个SVM中，一般是通过投票计数，最多的就属于哪一类。

---

 4  pytorch实战

        先给上github：https://github.com/kazuto1011/svm-pytorch

        原理繁琐，工程应用就很简单，就是一个二分类器，用torch.nn.linear（2,1）就好，但是训练loss就要自己写了。

优化目标 即loss： 

 这里使用hinge-loss

 loss = torch.mean(torch.clamp(1 - y * output, min=0))
 loss += args.c * (weight.t() @ weight) / 2.0

        torch.clamp(input , min, max ,out  = NONE) 

        使得输入在夹在[min , max]之间，这里就是一个hinge损失 L(x) = max ( 0 , 1-x)

        c 设置为了0.1，软间隔。