用人话讲明白支持向量机SVM(下)
文章目录
- 4.求解超平面
-
- 4.1几何间隔
- 4.2凸二次规划
- 4.3拉格朗日乘数法
- 5.线性可分问题小结
4.求解超平面
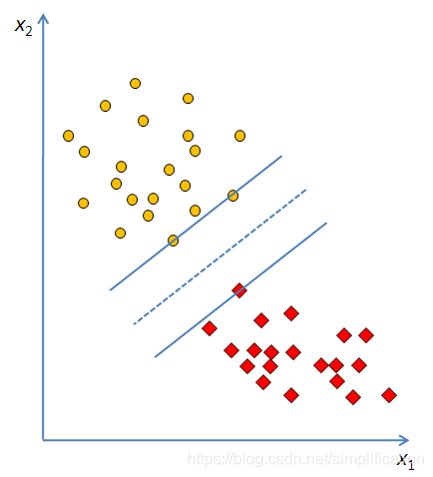
上篇仅介绍了SVM的基本概念,本篇着重讲解SVM中的最佳线性分类器(最大边界超平面)是如何求得的。
4.1几何间隔
上一小节给出二维问题下最佳线性分割的标准,就是分割线到两类边界点的距离最“宽”,那么这个“宽度”怎么量化和求解呢?
我们知道,点 ( x 0 , y 0 ) (x_{0} ,y_{0}) (x0,y0)到直线 A x + B y + c = 0 Ax+By+c=0 Ax+By+c=0的距离(中学的知识点),可以表示为:
D = ∣ A x 0 + B y 0 + c ∣ A 2 + B 2 D=\frac{|Ax_{0}+By_{0}+c|} {\sqrt{A^{2}+B^{2}}} D=A2+B2∣Ax0+By0+c∣
在我们的二维问题中,第i个点的坐标为 X i = ( x i 1 , x i 2 ) T X_{i}=(x_{i1},x_{i2})^{T} Xi=(xi1,xi2)T,直线为 w 1 x 1 + w 2 x 2 + b = W T X + b = 0 w_{1}x_{1}+w_{2}x_{2}+b=W^{T}X+b=0 w1x1+w2x2+b=WTX+b=0(为了打公式方便,后面我们不区分向量和其转置,省略T标志,统一写成 W X + b = 0 WX+b=0 WX+b=0),将上式替换, X i X_{i} Xi到分割直线的距离为:
D = ∣ W X i + b ∣ w 1 2 + w 2 2 = ∣ W X i + b ∣ ∣ ∣ W ∣ ∣ D=\frac{|WX_{i}+b|} {\sqrt{w_{1}^{2}+w_{2}^{2}}}=\frac{|WX_{i}+b|} {||W||} D=w12+w22∣WXi+b∣=∣∣W∣∣∣WXi+b∣
有的人也许对分母||W||感到陌生,这里多做点解释。
||W||是向量W的2-范数( L 2 L_{2} L2范数),一般我们说向量长度,指的是向量的2-范数。例如这里的 W = ( w 1 , w 2 ) W=(w_{1},w_{2}) W=(w1,w2),它的2-范数就是 ∣ ∣ W ∣ ∣ 2 = w 1 2 + w 2 2 ||W||_{2}=\sqrt{w_{1}^{2}+w_{2}^{2}} ∣∣W∣∣2=w12+w22 (通常会省略下标2,一般说||W||就是指 ∣ ∣ W ∣ ∣ 2 ||W||_{2} ∣∣W∣∣2),而它的p-范数( L p L_{p} Lp范数)就是 ∣ ∣ W ∣ ∣ p = w 1 p + w 2 p p ||W||_{p}=\sqrt[p]{w_{1}^{p}+w_{2}^{p}} ∣∣W∣∣p=pw1p+w2p 。
这里给出向量范数的一般形式:对于n维向量 W = ( w 1 , w 2 , . . . , w n ) W=(w_{1},w_{2},...,w_{n}) W=(w1,w2,...,wn),它的p-范数为:
∣ ∣ W ∣ ∣ p = w 1 p + w 2 p + . . . + w n p p ||W||_{p}=\sqrt[p]{w_{1}^{p}+w_{2}^{p}+...+w_{n}^{p}} ∣∣W∣∣p=pw1p+w2p+...+wnp
D = ∣ W X i + b ∣ ∣ ∣ W ∣ ∣ D=\frac{|WX_{i}+b|} {||W||} D=∣∣W∣∣∣WXi+b∣这个公式的学名叫做几何间隔,几何间隔表示的是点到超平面的欧氏距离(还记得上次讲线性回归时强调要记住这个名称吧?)。
以上是单个点到某个超平面的距离定义(在这个具体的二维例子中是一条直线,我们认为直线也是属于超平面的一种,后面统一写超平面的时候,不要觉得混乱哦)。上一节我们说要求最宽的“宽度”,最厚的“厚度”,其实就是求支持向量到超平面的几何间隔最大值。
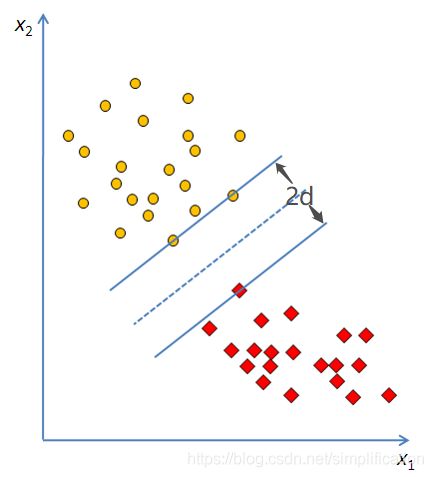
回到二维问题,令“马路宽度”为2d,即最佳分割线到两类支持向量的距离均为d,最佳分割线参数的求解目标就是使d最大。
4.2凸二次规划
假设L1是其中一条过+1类支持向量且平行于 W X + b = 0 WX+b=0 WX+b=0的直线,L2是过-1类支持向量且平行于 W X + b = 0 WX+b=0 WX+b=0的直线,这L1和L2就确定了这条马路的边边,L是马路中线。
由于确定了L的形式是 W X + b = 0 WX+b=0 WX+b=0,又因为L1、L2距离L是相等的,我们定义L1为 W X + b = 1 WX+b=1 WX+b=1,L2为 W X + b = − 1 WX+b=-1 WX+b=−1。为什么这两条平行线的方程右边是1和-1?其实也可以是2和-2,或者任意非零常数C和-C,规定1和-1只是为了方便。就像2x+3y+1=0和4x+6y+2=0是等价的,方程同乘一个常数后并不会改变。

确定了三条线的方程,我们就可以求马路的宽度2d。2d是L1和L2这两条平行线之间的距离:
2 d = ∣ 1 − ( − 1 ) ∣ ∣ ∣ W ∣ ∣ = 2 ∣ ∣ W ∣ ∣ 2d=\frac{|1-(-1)|}{||W||}=\frac{2}{||W||} 2d=∣∣W∣∣∣1−(−1)∣=∣∣W∣∣2
4.1小节我们讲了现在的目标是最大化几何间隔d,由于 d = 1 ∣ ∣ W ∣ ∣ d=\frac{1}{||W||} d=∣∣W∣∣1,问题又转化成了最小化||W||。对于求min||W||,通常会转化为求 m i n ∣ ∣ W ∣ ∣ 2 2 min\frac{||W||^{2}}{2} min2∣∣W∣∣2,为什么要用平方后除以2这个形式呢?这是为了后面求解方便(还记得上次讲线性回归讲到的凸函数求导吗?)。
||W||不可能无限小,因为还有限制条件呢。超平面正确分类意味着点i到超平面的距离恒大于等于d,即:
∣ W X i + b ∣ ∣ ∣ W ∣ ∣ ≥ d = 1 ∣ ∣ W ∣ ∣ \frac{|WX_{i}+b|}{||W||}\geq d=\frac{1}{||W||} ∣∣W∣∣∣WXi+b∣≥d=∣∣W∣∣1
两边同乘||W||,简化为:
∣ W X i + b ∣ = y i ( W X i + b ) ≥ 1 |WX_{i}+b|=y_{i}(WX_{i}+b)\geq 1 ∣WXi+b∣=yi(WXi+b)≥1
∣ W X i + b ∣ = y i ( W X i + b ) |WX_{i}+b|=y_{i}(WX_{i}+b) ∣WXi+b∣=yi(WXi+b)应该不难理解吧?因为y只有两个值,+1和-1。
- 如果第i个样本属于+1类别, y i > 0 y_{i}>0 yi>0,同时 W X i + b > 0 WX_{i}+b>0 WXi+b>0,两者相乘也大于0;
- 若属于-1类, y i < 0 y_{i}<0 yi<0, W X i + b < 0 WX_{i}+b<0 WXi+b<0,此时相乘依旧是大于0的。
这意味着 y i ( W X i + b ) y_{i}(WX_{i}+b) yi(WXi+b)恒大于0,y起到的作用就和绝对值一样。之所以要用y替换绝对值,是因为y是已知样本数据,方便后面的公式求解。
我们将这个目标规划问题用数学语言描述出来。
目标函数:
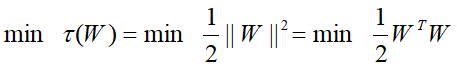
约束条件:
![]()
这里约束条件是W的多个线性函数(n代表样本个数),目标函数是W的二次函数(再次提醒,X、y不是变量,是已知样本数据),这种规划问题叫做凸二次规划。
什么叫凸二次规划?之前讲线性回归最小二乘法时,提到了处处连续可导且有最小值的凸函数。从二维图形上理解“凸”,就是在一个“凸”形中,任取其中两个点连一条直线,这条线上的点仍然在这个图形内部,例如 f ( x ) = x 2 f(x)=x^{2} f(x)=x2 上方的区域。
当一个约束优化问题中,目标函数和约束函数是凸函数(线性函数也是凸函数),该问题被称为凸优化问题。 当凸优化问题中的目标函数是一个二次函数时,就叫做凸二次规划,一般形式为:
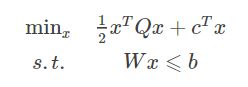
若上式中的Q为正定矩阵,则目标函数有唯一的全局最小值。我们的问题中,Q是一个单位矩阵。
4.3拉格朗日乘数法
这种不等式条件约束下的求多元函数极值的问题,到底怎么求解呢?
【以下涉及高等数学知识,推导过程较为复杂,数学基础较弱或对推导没兴趣的同学可以跳过,直接看第5小节】
当我们求一个函数 f ( x , y ) f(x,y) f(x,y)的极值时,如果不带约束,分别对x,y求偏导,令两个偏导等于0,解方程即可。这种是求无条件极值。
带约束的话则为条件极值,如果约束为等式,有时借助换元法可以将有条件转化为无条件极值从而求解,不过换元消元也只能解决三元以内的问题。而拉格朗日乘数法可以通过引入新的未知标量(拉格朗日乘数 λ \lambda λ),直接求多元函数条件极值,不必先把问题转化为无条件极值的问题。
求函数 f ( x , y ) f(x,y) f(x,y)在附加条件 φ ( x , y ) = 0 \varphi(x,y)=0 φ(x,y)=0下可能的极值点,可以先做拉格朗日函数:
 讲完拉格朗日乘数法的思路,仍解决不了上面的问题,因为该问题约束条件是不等式。其实,解决办法很简单,分成两部分看就行。
讲完拉格朗日乘数法的思路,仍解决不了上面的问题,因为该问题约束条件是不等式。其实,解决办法很简单,分成两部分看就行。
为了看起来简洁,我们令目标函数 m i n ∣ ∣ W ∣ ∣ 2 2 min\frac{||W||^{2}}{2} min2∣∣W∣∣2为 m i n f ( W ) minf(W) minf(W),约束条件 y i ( W X i + b ) − 1 ≥ 0 y_{i}(WX_{i}+b)-1\geq 0 yi(WXi+b)−1≥0为 g i ( W ) ≥ 0 g_{i}(W)\geq 0 gi(W)≥0。
- 当可行解W落在 g i ( W ) > 0 g_{i}(W)>0 gi(W)>0区域内时,此时的问题就是求无条件极值问题(因为极小值已经包含在整个大区域内),直接极小化 f ( W ) f(W) f(W)就行;
- 当可行解W落在 g i ( W ) = 0 g_{i}(W)=0 gi(W)=0区域内时,此时的问题就是等式约束下的求极值问题,用拉格朗日乘数法求解即可。
这两部分对应到样本上,又是什么?
- 当可行解落在 g i ( W ) > 0 g_{i}(W)>0 gi(W)>0内时,此时i这个样本点是“马路”之外的点;
- 当可行解落在 g i ( W ) = 0 g_{i}(W)=0 gi(W)=0内时,此时i这个样本点正好落在马路边上,也就是我们的支持向量!
我们再进一步思考下:
- 当可行解落在 g i ( W ) > 0 g_{i}(W)>0 gi(W)>0内时,此时约束不起作用(即求无条件极值),也就是拉格朗日乘数 λ i = 0 \lambda_{i}=0 λi=0;
- 当可行解落在边界上时, λ i ≠ 0 \lambda_{i}\neq 0 λi̸=0 , g i ( W ) = 0 g_{i}(W)=0 gi(W)=0。
不论是以上哪种情况, λ i g i ( W ) = 0 \lambda_{i} g_{i}(W)=0 λigi(W)=0均成立。
搞懂了上面说的,接下来构造拉格朗日函数,n个不等式约束都要加拉格朗日函数 λ i ≥ 0 \lambda_{i} \geq 0 λi≥0,有拉格朗日乘数向量 λ = ( λ 1 , . . . λ n ) T \lambda =(\lambda_{1},...\lambda_{n})^{T} λ=(λ1,...λn)T:
(1) L ( W , b , λ ) = f ( W ) − ∑ 1 n λ i g i ( W ) = ∣ ∣ W ∣ ∣ 2 2 − ∑ 1 n λ i y i ( W X i + b ) + ∑ 1 n λ i L(W,b,\lambda ) = f(W)-\sum_{1}^{n} \lambda_{i} g_{i}(W) \newline =\frac{||W||^{2}}{2} - \sum_{1}^{n} \lambda_{i}y_{i}(WX_{i}+b) +\sum_{1}^{n} \lambda_{i} \tag{1} L(W,b,λ)=f(W)−1∑nλigi(W)=2∣∣W∣∣2−1∑nλiyi(WXi+b)+1∑nλi(1)
要求极值,先对参数求偏导:
(2) ∂ L ∂ W = W − ∑ 1 n λ i y i X i = 0 \frac{\partial L}{\partial W}=W-\sum_{1}^{n} \lambda_{i}y_{i}X_{i}=0 \tag{2} ∂W∂L=W−1∑nλiyiXi=0(2)
(3) ∂ L ∂ b = ∑ 1 n λ i y i = 0 \frac{\partial L}{\partial b}=\sum_{1}^{n} \lambda_{i}y_{i}=0 \tag{3} ∂b∂L=1∑nλiyi=0(3)
此时又要引入一个概念——对偶问题(可见学明白SVM需要的数学知识真的很多,怪不得是机器学习入门的拦路虎呢),关于对偶问题,可以参见这篇文章,这里不赘述。简单而言,就是原先的问题是先求L对 λ \lambda λ的max再求对W、b的min,变成先求L对W、b的min再求 λ \lambda λ的max。
将(2)式 W = ∑ 1 n λ i y i X i W=\sum_{1}^{n} \lambda_{i}y_{i}X_{i} W=∑1nλiyiXi代入(1)式,得:
(4) L = 1 2 ( ∑ 1 n λ i y i X i ) ( ∑ 1 n λ i y i X i ) − ∑ 1 n λ i y i ( ( ∑ 1 n λ i y i X i ) X i + b ) + ∑ 1 n λ i = ∑ 1 n λ i − 1 2 ( ∑ i = 1 n ∑ j = 1 n λ i λ j y i y j X i T X j ) L = \frac{1}{2}(\sum_{1}^{n} \lambda_{i}y_{i}X_{i})(\sum_{1}^{n} \lambda_{i}y_{i}X_{i}) - \sum_{1}^{n} \lambda_{i}y_{i} ((\sum_{1}^{n} \lambda_{i}y_{i}X_{i})X_{i}+b) \newline +\sum_{1}^{n} \lambda_{i} = \sum_{1}^{n} \lambda_{i} - \frac{1}{2}(\sum_{i=1}^{n} \sum_{j=1}^{n} \lambda_{i} \lambda_{j}y_{i}y_{j}X_{i}^{T}X_{j}) \tag{4} L=21(1∑nλiyiXi)(1∑nλiyiXi)−1∑nλiyi((1∑nλiyiXi)Xi+b)+1∑nλi=1∑nλi−21(i=1∑nj=1∑nλiλjyiyjXiTXj)(4)
此时目标函数中W、b就都被消去了,约束最优化问题就转变成:
目标函数:
(5) m i n L ( λ ) = m i n ( 1 2 ∑ i = 1 n ∑ j = 1 n λ i λ j y i y j X i T X j − ∑ 1 n λ i ) minL(\lambda ) = min(\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} \lambda_{i} \lambda_{j}y_{i}y_{j}X_{i}^{T}X_{j}-\sum_{1}^{n} \lambda_{i} ) \tag{5} minL(λ)=min(21i=1∑nj=1∑nλiλjyiyjXiTXj−1∑nλi)(5)
约束条件:
(6) ∑ 1 n λ i y i = 0 , λ i ≥ 0 \sum_{1}^{n} \lambda_{i}y_{i}=0 , \lambda_{i} \geq 0 \tag{6} 1∑nλiyi=0,λi≥0(6)
(7) λ i ( y i ( W X i + b ) − 1 ) = 0 , i = 1 , 2... n \lambda_{i}( y_{i}(WX_{i}+b)-1) = 0, i=1,2...n \tag{7} λi(yi(WXi+b)−1)=0,i=1,2...n(7)
(6)式来自上面的(3)式,(7)式是由 λ i g i ( W ) = 0 \lambda_{i} g_{i}(W)=0 λigi(W)=0而来。如果能解出上面这个问题的最优解,我们就可以根据这个 λ \lambda λ求解出我们需要的W和b。
5.线性可分问题小结
最大边界超平面是由支持向量决定的,支持向量是边界上的样本点:
- 假设有m个支持向量,则 W = ∑ 1 m λ i y i X i W=\sum_{1}^{m} \lambda_{i}y_{i}X_{i} W=∑1mλiyiXi;
- 从m个支持向量中任选一个,可以求 b = y i − W X i b=y_{i}-WX_{i} b=yi−WXi;
- 决策函数 h ( x ) = S i g n ( W T X + b ) = S i g n [ ∑ 1 m ( λ i y i X i T ) X + b ] h(x)=Sign(W^{T}X+b)=Sign[\sum_{1}^{m} (\lambda_{i}y_{i}X_{i}^{T})X+b] h(x)=Sign(WTX+b)=Sign[∑1m(λiyiXiT)X+b];
- 对新样本 X ∗ X_{*} X∗的预测: S i g n ( W T X ∗ + b ) Sign(W^{T}X_{*}+b) Sign(WTX∗+b), W T X ∗ + b W^{T}X_{*}+b WTX∗+b为正则 y ∗ = 1 y_{*}=1 y∗=1,为负则 y ∗ = − 1 y_{*}=-1 y∗=−1,为0拒绝判断。
至此我们讲完了线性分类支持向量机的逻辑思想和求解过程,但这些只是SVM的基础知识,真正的核心其实还没有讲到。要知道,SVM的优势在于解决小样本、非线性和高维的回归和二分类问题(Support vector machine,SVM,1992, Boser, Guyon and Vapnik)。
- 小样本,是指与问题的复杂度相比,SVM要求的样本数相对较少;
- 非线性,是指SVM擅长应付样本数据线性不可分的情况,主要通过核函数和松弛变量来实现,这一块才是SVM的精髓。由于这一系列文章是我的机器学习入门笔记,所以暂时不会涉及,等入门系列结束后也许会更深入地研究;
- 高维,是指样本维数很高,因为SVM 产生的分类器很简洁,用到的样本信息很少,仅仅用到支持向量。由于分类器仅由支持向量决定,SVM还能够有效避免过拟合。
参考链接:
从超平面到SVM(一)
从超平面到SVM(二)
多元函数的极值及其求法
关于SVM数学细节逻辑的个人理解(二)
本文首发于知乎:机器学习笔记02-支持向量机SVM(下)