面试基础算法及编程 第二弹（链表相关：主要考察指针的应用）

// #  -*- coding:utf-8 -*- 
// #  @Author: Mr.chen([email protected]) 
// #  @Date: 2018-08-16 16:35:13 

// 注：此为第二弹，主要讲解链表相关面试笔试题，要求手写
// 注意，在涉及到链表的时候，形参传递链表头指针过来的时候，如果在函数中需要改变
// 头结点的指向，则需要传递二级指针， **，否则，不能改变其指针的指向

#include 
#include 

// 节点结构体定义如下： 
struct ListNode 
{
    int m_value;
    ListNode * m_pNext;
};

/* 
1、向链表结尾添加一个节点, 如果该链表就是一个空链表时，即头结点就是该值的节点，因此可能改变头指针
   故需要传递一个 二级指针
*/
void AddToTail(ListNode ** pHead,int value)
{
    ListNode * pNew = new ListNode();
    pNew->m_value = value;
    pNew->m_pNext = NULL;
    
    //判断传递过来的是否是空链表
    if(NULL == *pHead)
    {
        *pHead = pNew;
    }
    else 
    {   
        // 定义一个栈对象指针指向头指针指向的头结点
        ListNode *pNode = *pHead;
        while(pNode->m_pNext != NULL)
            pNode = pNode->m_pNext;
        
        // 找到链表结尾
        pNode->m_pNext = pNew;
    }
}


/* 
2、在链表中找到第一个含有该值的节点，并且删除它 
*/
void RemoveNode(ListNode ** pHead,int value)
{
    if(NULL == pHead || NULL == *pHead)
        return;
    ListNode * pDeleted = NULL;
    if((*pHead)->m_value == value)
    {
        pDeleted = *pHead;
        *pHead = (*pHead)->m_pNext;
    }
    else 
    {
        ListNode *pNode = *pHead;
        while(NULL != pNode->m_pNext && pNode->m_pNext->m_value != value)
            pNode = pNode->m_pNext;
        if(NULL != pNode->m_pNext && pNode->m_pNext->m_value == value)
        {
            pDeleted = pNode->m_pNext;
            pNode->m_pNext = pNode->m_pNext->m_pNext;
        }
    }

    if(NULL != pDeleted)
    {
        delete pDeleted;
        pDeleted = NULL;
    }
}


/* 
3、输入一个链表的头结点，从尾到头打印出每个节点的值，一般会想到如果翻转链表的指向，
   在打印应该比较简单，但是打印输出一般只是只读属性，不建议改变原链表结构，可考虑
   栈结构，实现先进后出，或者使用递归（递归的本质就是栈结构）
*/

// 法一、使用栈结构
void printListReverse(ListNode *pHead)
{
    std::stack nodes;
    ListNode * pNode = pHead;
    
    while(NULL != pNode)
    {
        nodes.push(pNode);
        pNode = pNode->m_pNext;
    }

    while(!node.empty())
    {
        pNode = node.top();
        std::cout<< pNode->m_value <m_pNext)
            printListReverse(pHead->m_pNext);

        std::cout<< pHead->m_value <m_pNext)
    {
        ListNode * pNext = pDeleted->m_pNext;
        pDeleted->m_value = pNext->m_value;
        pDeleted->m_pNext = pNext->m_pNext;
        delete pNext;
        pNext = NULL;
    }
    //链表只有一个节点，既是头节点也是尾节点,这里涉及到要改变头结点的操作，故实参为二级指针 **
    else if (*pHead == pDeleted)
    {
        delete pDeleted;
        pDeleted = NULL;
        *pHead = NULL;
    }
    //链表中有多个节点，删除尾节点
    else
    {
        ListNode * pNode = *pHead
        // 找到上一个删除节点的上一个节点
        while(pDeleted != pNode->m_pNext)
            pNode = pNode->m_pNext;
        
        pNode->m_pNext = NULL;
        delete pDeleted;
        pDeleted = NULL;
    }
}


/* 
5、输出链表中倒数第 K 个节点，默认尾节点即是倒数第一个，此题典型的应该用前后指针来做，
   它和判断链表是否有环思路类似(两个指针移动速度不一样)，但是应该注意的就是代码的 【鲁棒性】，
   应该考虑各种异常情况，如，传入的头指针 pHead 为空，链表的节点数小于 k,以及 k 等于 0，
   等三种异常情况。（a先走 k-1步，然后 a, b一起移动，速度一样）
*/
ListNode * FindKthToTail(ListNode *pHead,unsigned int k)
{
    if(NULL == pHead || k == 0)         // 异常情况考虑
        return NULL;
    ListNode *pa = pHead;
    ListNode *pb = NULL;
    for (unsigned int i=0; i < k - 1; ++i)
    {
        if(NULL != pa->m_pNext)         // 异常情况考虑，length < k
            pa = pa->m_pNext;
        else 
            return NULL;
    }
    pb = pHead;
    while(NULL != pa->m_pNext)
    {
        pa = pa->m_pNext;
        pb = pb->m_pNext;
    }
    return pb;
}


/* 
6、翻转链表，强调点【代码的鲁棒性】,与其很快的写出一个漏洞百出的代码，不如仔细分析在写出一个鲁棒的代码。
   面试者怎么避免错误呢，一个很好的办法就是提前想好测试用例，其实，面试官检查面试者的代码也是用他事先
   准备好了的测试用例，如果我们可以事先想到那么就很好了。

   一般涉及到链表的题，都是想考察面试者的操作指针的能力，在本题目中如果不引入额外的空间复杂度，则直观的
   想法就是直接在原链上翻转指向，就会涉及到一个链表断裂的问题，我们把链表抽象成前中后三段，只研究其中的
   任意三个点的时候（如 h,i,j），发现在 while 循环中去改变指向时，为了记住节点状态，不让链表断掉，我们
   至少需要三个指针，分别指向当前的节点以及它前一个节点，以及后一个节点。最后在翻转之后我们需要返回新的
   头结点，其实新的头结点就是原链表的尾节点，即原链表中pNext 指向为 NULL的节点。

   本题的测试用例，可以是如下:
   * 输入的链表头指针为 NULL
   * 输入的链表只有一个节点
   * 输入的链表有多个节点 
*/

// 法一：迭代法
ListNode *ReverseLinkList(ListNode *pHead)        
{
    ListNode *pReverseHead = NULL;
    ListNode *pNode = pHead;
    ListNode *pPrev = NULL;

    while(pNode)
    {
        ListNode* pNext = pNode->m_pNext;
        if(NULL == pNext)
            pReverseHead = pNode;
        
        pNode->m_pNext = pPrev;
        pPrev = pNode;        
        pNode = pNext;
    }
    return pReverseHead;
}   // 此题虽然代码不长，但是仍需要理清楚其中的逻辑关系

// 法二：递归（类似栈功能）实现,即就不用循环了    注：在文末可查看图解。 
ListNode *ReverseLinkList(ListNode *pHead)
{
    if(pHead == NULL || pHead->m_pNext == NULL)
    {
        return pHead;     // 若链表为空，就直接返回，若 pHead->m_pNext 为 NULL，则为最后一个节点，为递归出口,返回一次。
    }
    ListNode *pNewHead = ReverseLinkList(pHead->m_pNext);     //新头结点始终指向原链尾节点
    pHead->m_pNext->m_pNext = pHead;                          // 翻转链表的指向
    pHead->m_pNext = NULL;                                    // 新的尾节点赋值为 NULL
    return pNewHead;                                          // 返回头结点
}

/* 
7、合并两个递增排序链表，注意一：异常情况（鲁棒性）。注意二：想清楚在写代码，当我们用两个指针分别指向原
   链表时，在依次比较谁小，将小的合并到已经合并的链上。典型的是一个递归的思想。
*/
ListNode *Merge(ListNode *pHead1,ListNode *pHead2)
{
    // 异常值检测
    if(NULL == pHead1)
        return pHead2;
    else if(NULL == pHead2)
        return pHead1;
    
    ListNode *pMergeHead = NULL;
    // 开始递归
    if(pHead1->m_value < pHead2->m_value)
    {
        pMergeHead = pHead1;
        pMergeHead->m_pNext = Merge(pHead1->m_pNext,pHead2);
    }
    else  
    {
        pMergeHead = pHead2;
        pMergeHead->m_pNext = Merge(pHead1,pHead2->m_pNext);
    }
    return pMergeHead;
}


/* 
8、输入两个链表，找出它们的第一个公共节点，此题有三种思路：法一:蛮力法，轮循链表一的每一个节点的时候
   去轮循另外一个链表的每一个节点，比较是否相同，时间复杂度O(mn), 法二：如果俩个链表有公共节点，则它
   的拓扑结构一定是 Y ,故我们换一种思路，从两个链表的最后的节点开始比较，一直到最后一个相同的节点，即
   为相交节点的入口，但是对于单链表，想要找到最后的节点，从后面比较，即后进先比较。故我们可以分别用两个
   栈去存储，故时间复杂度为O(m+n),空间复杂度也为O(m+n)。法三：（也是推荐方法）其实从拓扑关系可知，主要
   是考虑到两个链长不一样，不能依次 ++，然后比较。故我们可以采取两次遍历的方法，第一次遍历先计算两个链
   的长度，如a链比b链长多少n。第二次遍历的时候，让长的先走n步，然后在两个链的指针一起走，找到第一个相同
   的节点，即为相交的第一个公共节点。时间复杂度为 O(m+n),相比第二个方法没了空间复杂度。 
*/

//先定义计算链长的函数
unsigned int GetListLength(ListNode *pHead)
{
    unsigned int nLength = 0;
    ListNode * pNode = pHead;
    while(pNode != NULL)
    {
        ++nLength;
        pNode = pNode->m_pNext;
    }
    return nLength;
}

ListNode *FindFirstCommonNode(ListNode *pHead1,ListNode *pHead2)
{
    // 获取链表的长度
    unsigned int nLength1 = GetListLength(pHead1);
    unsigned int nLength2 = GetListLength(pHead2);
    
    // 获取差值
    int nLengthDif = nLength1 - nLength2;
    ListNode *pHeadLenthLong = pHead1;
    ListNode *pHeadLenthShort = pHead2;
    if(nLength2 > nLenght1)
    {
        pHeadLenthLong = pHead2;
        pHeadLenthShort = pHead1;
        nLengthDif = nLength2 - nLength1;
    }

    // 先在长链上先走几步
    for(int i=0; i< nLengthDif; i++)
        pHeadLenthLong = pHeadLenthLong->m_pNext;
    
    // 然后一起遍历
    while((pHeadLenthLong != NULL) && (pHeadLenthShort != NULL) && (pHeadLenthLong != pHeadLenthShort))
    {
        pHeadLenthLong = pHeadLenthLong->m_pNext;
        pHeadLenthShort = pHeadLenthShort->m_pNext;
    }
    
    // 得到第一个公共节点
    ListNode *pFirstCommonNode = pHeadLenthLong;
    return pFirstCommonNode;
}



/* 
9、圆圈中最后剩下的数字（约瑟夫环问题），0,1,····, n-1,这 n 个数字排成一个圆圈，从数字 0 开始每次从
   圆圈中删除第 m 个数字，求出这个圆圈里面的最后一个数字。例如：0, 1, 2, 3, 4 这五个数字组成一个圆圈
   ，从 0 开始每次删除第三个数字，则删除的前四个数字依次是 2，0, 4，1 。因此，最后剩下的数字是 3。

   解决这个问题，这里介绍两种方法，法一：经典的方法，用环形链表模拟圆圈，开始游戏。法二：建立数据模型
   ，利用数字规律，用数学的方法去解决它，直接计算出最后剩下的数字。法一：如果面试官允许，可以用标准模板
   库 std::list 去模拟，不过，为了让其具有循环链表的特性，需要每次遍历到尾节点的时候，迭代器回到起始节
   点（代码如下）。法二(如下描述使用语言有不当之处，首先 f(m,n) 应该是代表的是一个处理过程，计算机科学是对过程的抽象，其次在寻找递推公式时，是想让问题规模变小而需要保持输入模式一样，故而寻找了两个仿射变换，最后找到递推公式，使用递归或迭代都可以实现该算法。)： 首先我们定义一个关于 n和m 方程 f(m,n)，表示在 n 个数字，0,1,····,n-1。每次
   删除第 m 个数字最后剩下的数字。在其中，第一个删除的数字是 （m-1) % n。为了简单起见，我们把它记为 k,
   那么删除第 K 个数字后，剩下的 n-1 个数字为 0,1,····, k-1, k+1, ····, n-1,并且下一次从 k+1 开始计
   数，相当于形成了如下序列: k+1, ····, n-1, 0,1,····, k-1。该序列最后剩下的序列也是关于 n, m 的函数，
   但是由于不是从 0,开始故有别于前面的函数模型，我们暂且记为 f'(n-1,m),由题意可知，在一次删除一个元素后
   ，虽然序列顺序变了，但是可以知道， f(m,n) = f'(n-1,m)。 接下来，我们对剩下的序列做一个仿射映射（或者
   说平移映射）即：k+1 --> 0 , k+2 --> 1, ···, k-1 --> n-2。定义映射函数p, p = (x-k-1) % n,其中x是
   映射前，ｐ为映射后。它的逆映射为　ｐ'(x) = ( x+k+1 )% n, 映射之后我们可以发现它与最开始我们建立的模
   型，序列一致了,故可以用 f 函数来表示，故映射之前序列中剩下的数字 f'(n-1,m) = p'[f(n-1,m)] = 
   [f(n-1,m) + k +1]% n ,带入K = (m -1)%n ,可得 f(n,m) = f'(n-1,m) = [f(n-1,m) + m]% n, 边界，当
   n = 1时，只有 0 故最后剩下的只有 0，我们把这种关系表示为 f(n,m) =  0, n=1. f(n,m) = [f(n-1,m) + m]% n, n>1
   ,于是，我们就可以用递归或者循环来实现了，时间复杂度为O(n),空间复杂度为 O(1).
   循环链表的应用，重点考察抽象建模的能力（建立数学模型，然后尝试用经典的编程思想和数学方法去解决它）。
*/

// 法一：循环链表
int LastRemain(unsigned int n,unsigned int m)
{
    if( n< 1 || m < 1)
        return -1;
    unsigned int i = 0;
    
    //定义链表
    std::list numbers;
    for (i = 0; i< n; ++i)
        numbers.push_back(n);
    list::iterator current = numbers.begin();
    while(numbers.size() > 1)
    {
        // 找到 m 的位置
        for(int i = 1; i::iterator next = ++ current;
        if(next == numbers.end())
            next = numbers.begin()
        
        -- current;
        numbers.erase(current);
        current = next;
    }
    return *(current); 
} //每删除一个数字，需要 m步计算，共 n 个数字，故总的时间复杂度为O(mn),空间复杂度为O(n)


// 法二：抽象 + 建模 用数学方法解答（原理基于上面解答）
int LastRemaining(unsigned int n,unsigned int m)
{
    if(n<1 || m<1)
        return -1;
    // 边界 n = 1时，最后为 0
    int last = 0;
    for(int i=2; i<=n ;i++)
    {
        last = (last + m) % i;
    }
    return last;
}


/* 
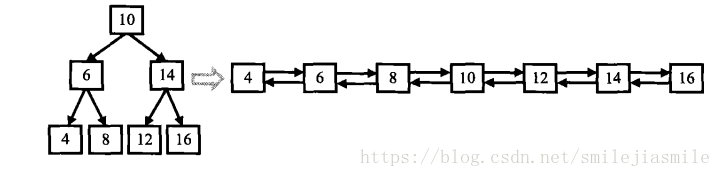
10、二叉搜索树和双向链表，要求：输入二叉搜索树，将二叉搜索树转换成排序的双向链表。
    要求不能创建新的节点，只能调整树中节点指针的指向，比如：如下图中所示，输出排
    序后的双向链表。二叉搜索树也是一种排序的数据结构，并且每个节点也有两个指向子
    节点的指针，故理论上是可以进行相互转换的，在二叉搜索树中，左子节点的值小于父
    节点，右子节点的值大于父节点，故我们可以将指向左子节点的指针改为指向前一个节
    点的指针，将指向右子节点的指针改为指向后一个节点的指针。具体方法如下：由于中
    序遍历二叉搜索树，得到的便是一个排好序的序列，故当我们遍历到根节点的时候，需
    要将其看成三个部分，对于图中的值为 10 的根节点，根节点为 6 的左子树，根节点
    为 14 的右子树，由排序链表的定义，节点10 将会和左子树中最大的一个节点（8）链
    接，和右子树中最小的一个节点（12）链接，按照中序遍历的特点，当我们遍历到根节
    点时，它的左子树已经转换成了一个排序的链表，并且最后一个节点是当前最大节点，
    此时我们只需要将根节点链接到该有序链表的后面，并且将尾指针指向新的尾节点，在
    链接上右子树已经排好序的有序链表，即可完成转换。至于左右子树怎么转换，我们可
    以很容易的想到递归的思想。
*/

 

// 二叉节点树的节点定义如下：
struct BiTreeNode 
{
    int         m_value;
    BiTreeNode* m_pLeft;
    BiTreeNode* m_pRight;
};

BiTreeNode* Convert(BiTreeNode* pRootofTree)
{
    BiTreeNode* pLastNodeInList = NULL;
    
    //开始转换
    ConvertNode(pRootofTree,&pLastNodeInList);

    // pLastNodeInList 指向双向链表的最后一个节点，但我们需要返回头结点
    BiTreeNode* pHeadofTree = pLastNodeInList;
    while(pHeadofTree != NULL && pHeadofTree->m_pLeft != NULL)
        pHeadofTree = pHeadofTree->m_pLeft;
    
    //返回头节点
    return pHeadofTree;
}

void ConvertNode(BiTreeNode* pNode,BiTreeNode** pLastNodeInList)
{
    if(NULL == pNode)
        return;

    BiTreeNode* pCurrent = pNode;
    // 找到最左边的节点
    if(pCurrent->m_pLeft != NULL)
        ConvertNode(pCurrent->m_pLeft,pLastNodeInList);
    
    //改变左指向,如果尾节点不为 NULL，增加右指向，最后更新尾指针指向
    pCurrent->m_pLeft = *pLastNodeInList;
    if(*pLastNodeInList != NULL)
        (*pLastNodeInList)->m_pRight = pCurrent;
    *pLastNodeInList = pCurrent;         // 注意，这里要改变pLastNodeInList 的指向由于是二级指针，故需要解引用 *

    // 判断是否有右子树
    if(pCurrent->m_pRight != NULL)
        ConvertNode(pCurrent->m_pRight ,pLastNodeInList);
}