【CVPR2020】网络结构：GhostNet/频域卷积/Pi-Net

轻量网络：GhostNet

文章来源 https://arxiv.org/pdf/1911.11907.pdf

Intuition
1， CNN的特征图往往含有冗余的信息
2，冗余的信息可能是网络表现好的关键
3，这些冗余的信息可以通过更简单的计算得到
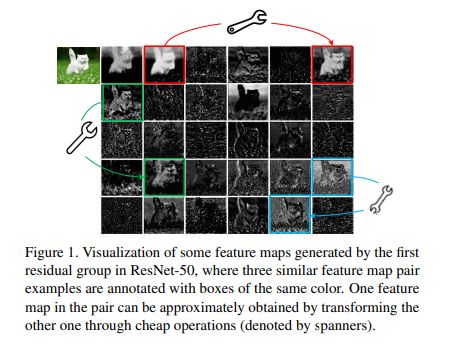
下图列举了三组相似的特征图，每组两张。可以通过简单的线性计算使其中一张特征图转换为另一张

Network
设s张特征图可以分为一组。则每组只需一张特征图(暂称为标准特征图)由普通的方式得到，其他的可以用这一张特征图再做卷积(不带激活层)得到。

设输入特征图$c\times h\times w$,输出特征图$n\times h^{\prime }\times w^{\prime }$,原始输入的卷积核大小$k\times k$，标准特征图的卷积核大小$d\times d$，则
理论加速比

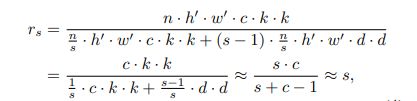
理论压缩比

约等号成立的条件是d和k相近，且s远小于c。
在这个思想上建立bottleneck如下

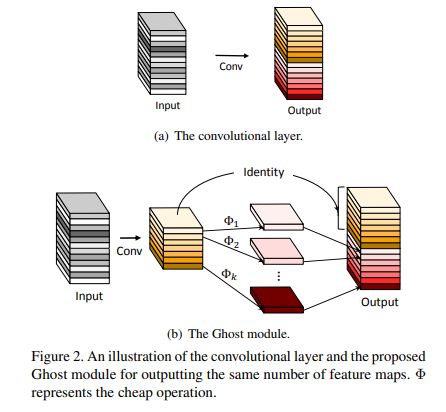
my opinion
1，文中有一个观点“冗余的信息可能是网络表现好的关键”，对此似乎既没有引用文献也没有做实验证明。
2，为什么要用线性变换进行特征图之间的迁移呢？难道线性变换足够了嘛?
3，看网络结构不就是分组卷积+concat嘛，看官方源码果然。。。

class GhostModule(nn.Module):
    def __init__(self, inp, oup, kernel_size=1, ratio=2, dw_size=3, stride=1, relu=True):
        super(GhostModule, self).__init__()
        self.oup = oup
        init_channels = math.ceil(oup / ratio)
        new_channels = init_channels*(ratio-1)

        self.primary_conv = nn.Sequential(
            nn.Conv2d(inp, init_channels, kernel_size, stride, kernel_size//2, bias=False),
            nn.BatchNorm2d(init_channels),
            nn.ReLU(inplace=True) if relu else nn.Sequential(),
        )

        self.cheap_operation = nn.Sequential(
            nn.Conv2d(init_channels, new_channels, dw_size, 1, dw_size//2, groups=init_channels, bias=False),
            nn.BatchNorm2d(new_channels),
            nn.ReLU(inplace=True) if relu else nn.Sequential(),
        )
    def forward(self, x):
        x1 = self.primary_conv(x)
        x2 = self.cheap_operation(x1)
        out = torch.cat([x1,x2], dim=1)
        return out[:,:self.oup,:,:]

频率域卷积

文章来源：https://arxiv.org/pdf/2002.12416.pdf

Motivation
现在图像的分辨率越来越高，而CNN受限于计算量和存储，经常要把输入图像resize到一个固定的尺寸(比如224x224)，这就不可避免地带来信息损失。
本文将图像用离散余弦变换(DCT)到频率域，再丢掉一些冗余的频率，从而压缩图像，在此基础上做卷积操作。输入变小了可以带来一系列好处，比如减少计算量和CPU/GPU通信带宽

Process

上图展示了空间域变频率域的流程。先将图像转为YCbCr格式，再对三个通道做DCT(和JPEG编码一样)，相同频率的分量在相同的通道。从中选出比较有代表性的通道组成输入。
Learning-based Frequency Channel Selection
下面是动态选择通道的方式。根据这种方法，不同的数据可能会选择不同的通道。

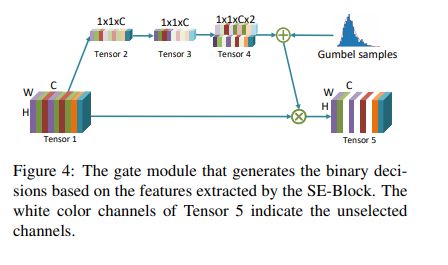
利用类似se模块的门控机制来筛选具有代表性的通道。设输入Tensor 1的维度为$W\times H\times C$，先全局平均池化成Tensor 2，再用1x1的卷积变成Tensor 3。此时Tensor 3 的维度是$1\times 1\times C$。 Tensor 3在分别乘两个变量得到两个输出，这两个输出拼在一起组成$1\times 1\times C\times 2$的Tensor 4, 表示通道权重为0或1的概率。比如第i个通道在Tensor 4 的两个值分别为7.5和2.5，就意味着75%的概率第i个通道应该从输入中丢掉，利用伯努利分布，第i个通道的权重有75%的概率是0，有25%的概率是1，不可以是其他值。最后第i个通道要乘以这个权重才输入后面的网络中。

让输入$x=(x_1,x_2,\cdots ,x_C)$,$F(x_i)$表示$x_i$的权重，$F(x_i)$= 0 or 1. 为了让丢掉的通道更多，即$F(x_i)$=0的概率更大，在损失函数后面加一正则项

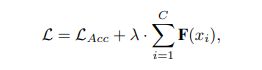
Static Frequency Channel Selection
下面是固定选择通道的方法。
本问先研究了哪些频率的分量有更大的概率被选中。下图是ImageNet和COCO上的热力图：

每个格子的数值表示频率，颜色深浅表示被选中的概率。
从上图可以得出三点结论：1，低频分量更易被选中，可能是因为低频分量含有更多的信息 2，Y更易被选中，同理可能是因为亮度含有更多的信息 3，ImageNet 和COCO的热力图分布相似，说明可以泛化，固定选择通道是合理的。
有趣的是，JPEG压缩标准也是用更多的比特表示低频分量和Y通道，不谋而合。
my opinion
将空间域的算法套频率域的论文已经有很多了。将待学习特征变换到频率域，低频分量带有更多的信息，高频分量带有更细节的信息。但究竟哪个频率对分类最有帮助，取决于特征的性质。之前做过类似的工作，我的一个直觉上的结论是，如果特征在空间上的分布越集中，则越高频的分量更有利于分类。比如人脸和ImageNet，最利于分类的频率往往前者的更高。

多项式网络：$\Pi$-Net

本文提出了多项式网络，拥有比CNN更强大的表达能力。
这个有空再读吧。