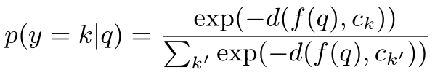近五年few-shot learning模型 | 元学习 | Meta-Learning综述

借鉴《Automated human cell classification in sparse datasets using few-shot learning》这篇文章，大概了解了few-shot learning的一些模型。这篇文章于2022.2.21发表在scientific reports上，是Nature的 子刊，综合3区，3年平均IF为4.13。
本文第一部分会介绍一下这篇文章，第二部分介绍一下基于优化的（MAML、Reptile）、基于度量的（Prototypical Networks、PT+MAP、LaplacianShot 、SimpleCNAPS ）、基于度量增强的（EPNet 、S2M2、AmDimNet）小样本学习方法与举例。

1 关于文章

1.1 通用背景

人体细胞分类与分子性质预测面临同样的问题，那就是数据稀少。

1.2 本文工作

① 研究了few-shot learning在人体细胞分类中的应用。
用 few-shot learning 方法在non-medical数据集上训练，在medical数据集上测试，精度至少下降了30%。
② 改变 backbone architecture 与 train scheme，探究是否有作用。
修改主干架构和训练方法，EPNet的准确率从88.66%下降到44.13%。
③ 提出该领域未来的研究方向。
小样本学习在 人体细胞分类领域 表现不佳，修改现有网络架构的尝试并不有效，未来的研究工作应侧重于 使用基于优化的方法 或 自监督学习方法。

1.3 数据集

train：Mini-ImageNet few-shot dataset
test：BCCD 白细胞数据集 && HEp-2 细胞数据集

mini-ImageNet：是来自ImageNet的类子集的下采样版本。该数据集总共包含 100 个类，分为训练、验证和测试类拆分
HEp-2 细胞数据集：喉癌上皮细胞数据集

1.4 实验结果

1.4.1 在Mini-ImageNet上训练，在BCCD与HEp-2上测试。

100个epoch足以让模型收敛，大约在60-80个epoch之间模型达到收敛

1.4.2 在BCCD上训练，在HEp-2上测试。

为了进一步探索基于细胞图像的few-shot learning的性能，使用HEp-2作为训练数据集，BCCD作为测试数据集，进行了域内训练和测试。（HEp-2被选为训练集因为类别更多，HEp-2有6个类， BCCD有五个类）

使用了第一个实验中表现最好的模型（BCCD上的Reptile 和 HEp-2上的EPNet）

1.4.3 换主干结构

替换EPNet的主干结构（backbone architecture），所有选定替换的主干网络 都未能匹配或超过原始的WideResNet主干网络。
原网络depth 28 and width 10。

宽度width——每层的通道数
深度depth——神经网络的层数

---

---

---

---

---

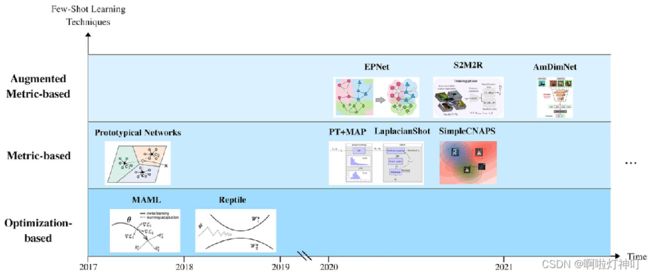
2 关于 Few-shot Learning Techniques

从下往上分别是基于优化的方法、基于度量的方法、基于度量增强的方法：
“Optimization-based”基于优化的方法：对网络采用优化的过程进行更改。
“Metric-based”基于度量的方法：获得一组样本之间的相似性得分。
"Augmented Metric-based“基于度量增强的方法：对基于度量的小样本学习技术进行增强，如应用自监督或者转导过程。
（图来自于《Automated human cell classification in sparse datasets using few-shot learning》）

2.1 Optimization-based 基于优化的方法

基于优化的小样本学习方法 没有利用模型依赖的外部度量指标，取而代之的是利用模型不可知（model-agnostic ）方法，即利用基于随机梯度下降的学习方法，定义一个与所有模型兼容的通用优化方法。通过应用该算法，所有潜在的类都得到了优化，而不是只针对某个数据集的优化。
设通用模型为fθ，参数为θ，通用损失函数为L，任务Ti为一组类从数据集中的采样。使用定义的变量，可以使用以下等式通过随机梯度下降进行迭代更新：

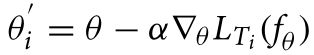
然而，这样做时，计算的是单个任务中单个批次的损失。基于优化的方法，例如 MAML 和 Reptile，可以提高所有给定任务的准确性，而不是单个任务。

随机梯度下降法SGD（stochastic gradient descent）：对每个数据都计算算一下损失函数，然后求梯度更新参数。SGD可以看作是MBGD（小批量梯度下降法mini-batch Gradient Descent）的一个特例，即batch_size=1的情况。在深度学习及机器学习中，基本上都是使用的MBGD算法。优点：计算速度快；缺点：收敛性能不好。

下面介绍一些基于优化的算法的典型模型。

2.1.1 MAML

源于论文：Model-Agnostic Meta-Learning for Fast Adaptation of Deep Network
传送门：https://arxiv.org/pdf/1703.03400.pdf

①MAML的运作过程：
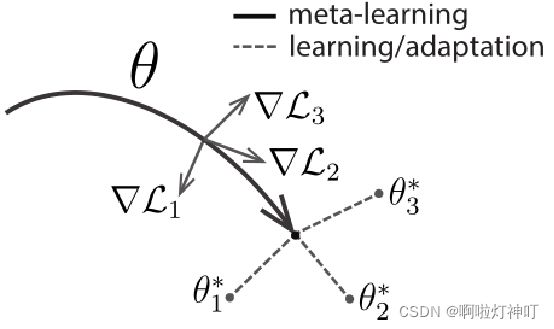
MAML是一个用来找初始化参数θ的方法，它聚焦于模型的初始化。假设我们有一个可以用在所有任务上的初始化参数θ，它经过每一个任务T_i都会被对应地更新成θ_i，形成任务T_i的专属参数。换句话说，如果有一个非常好的初始化参数θ，它能每次只优化一步或几步就会很快地变成θ_i，并且在新任务上实现非常好。

②简而言之，MAML做的事情就是：找到这样一个θ，以这个θ为初始状态，在其他几个task上行微调得到θ‘，计算loss(θ’)，然后把这loss(θ’)求和。如果这个sum（loss(θ’)）已经收敛于一个很小的值了，那么这个θ就是我们要的θ。
MAML算法优化初始化参数θ，它可快速适应新任务。对于新任务而言，这个点不一定是最好的，但具有较高的sensitivity，可以做fast adaptation。

③算法介绍：这是对于所有任务都通用的算法，首先需要有所有任务的一个分布p，里面一般设有train、test、validation，对分类任务而言，它们的class是不相交的，α和β是梯度下降的学习率。
1：首先随机初始化θ
3：抽样一个batch的所有task（如果batch size=4那就有4个task）
4：5：6：对于每一个task，在support中的k个样本上面计算他的loss的梯度，并:使用梯度下降将θ更新为适应每个任务的θ’
8：最后，使用一个batch中所有task的 梯度和 的 平均来更新θ（实际上用的是θ’在query上的loss的梯度，见算法2）

【Q】如何评价初始化参数θ的好坏？
【A】看他更新为θ_i 之后，在该任务T_i上的表现如何，这个表现如何用可以用损失函数来评价。每次，我们输入一个batch的tasks，然后利用初始化参数θ，在这个batch里所有的任务上更新，更新完毕后把这些task上的损失值加起来，得到大的Loss，这个大的Loss就可以评价我们初始θ的好坏。通过优化(update,8)找到最好的初始化参数θ，有了一个好的初始化参数θ，当我们遇到一个新的问题，模型就能很快地根据新任务做调整，只要一步或者几步的更新，就能有很好的结果。

2.1.2 Reptile

源于论文：On First-Order Meta-Learning Algorithms
传送门：https://arxiv.org/pdf/1803.02999.pdf

①核心思想：Reptile 是在每个单独的任务执行 k 次训练后，就开始真正更新网络模型的参数（Meta），更新方式不是梯度下降，但是和梯度下降公式长得很像，是用上一次的参数 θ 和 k 次后的参数 θ ̃ 的差来更新，更新的步长是ϵ 。在这个过程中，只有一阶求导的计算，就是在任务内部执行 k 次更新的过程中用到的随机梯度下降，这也是为什么标题中叫 First-Order 的原因。

②算法：
1 首先初始化一个网络模型的所有参数 θ
2 迭代 N 次，进行训练，每次迭代执行：
①随机抽样一个任务 T，用网络模型进行训练，对应的loss 是 Lt， ，训练结束后的参数是 θ
​ ②在参数 θ 上使用 SGD 或 Adam 执行K次梯度下降更新，得到 θ ̃
③ 用 θ ̃ 更新网络模型模型参数，θ = θ + ϵ ( θ ̃ − θ )
3 完成上述N次迭代训练，则结束整个过程

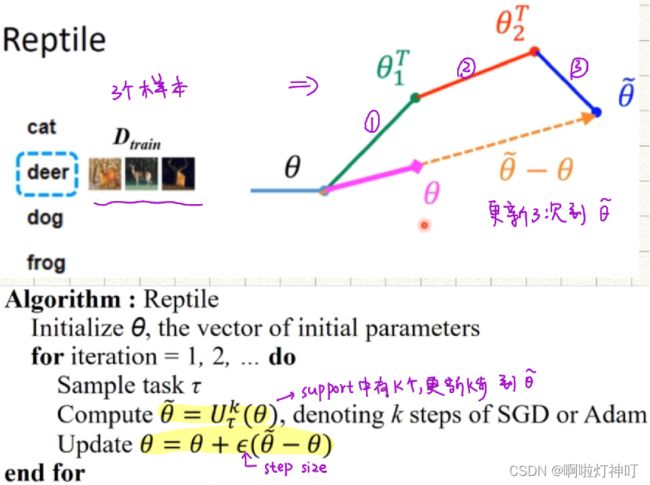
2.1.3 MAML VS Reptile

MAML需要使用Support和Query两次更新参数
而Reptile只需要更新一次参数

2.2 Metric-based 基于度量的方法

小样本学习中一些早期的方法利用基于度量的分析生成两个样本之间的相似性得分。在一般层面上，将KNN用在给定数据集上可以被认为是一种基本的、基于度量的小样本学习模型。
基于度量的模型考虑输入数据的相似性，基于标记数据（support set）的信息对未标记信息（query set）进行聚类.

2.2.1 Prototypical Networks

源于论文：Prototypical Networks for Few-shot Learning
传送门：https://arxiv.org/pdf/1703.05175.pdf

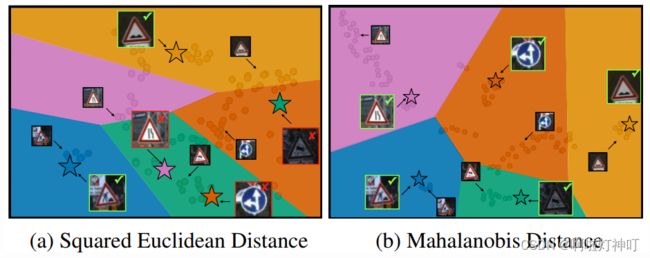
原型网络（ Prototypical Networks），使用嵌入函数将 support set 与 query set 映射到嵌入空间，support set 中的每个类的平均值被定义为原型向量，query embedding 与 原型向量之间的平方欧几里得距离用来生成给定 query point 的最终分布。

算法如下：

2.2.2 PT+MAP （MAML的改进）

源于论文：Leveraging the Feature Distribution in Transfer-based Few-Shot Learning
传送门：https://arxiv.org/pdf/2006.03806.pdf

背景：
基于迁移结构（也叫backbone结构）：通常训练的域与实际的域并不相同。所以，使用backbones提取的特征向量的分布非常复杂。因此，数据分布的强假设 会使得其方法不能很好的利用提取出的特征。所以，从两个方面解决了基于迁移的小样本学习问题。

文章idea：
文章主要提出了两点改进：
①Preprocessing the data extracted from the backbone so that it fits a particular distribution (i.e. Gaussian-like). 预处理提取的特征使其服从一定的分布。
②Leveraging this specific distribution thanks to a well-thought proposed algorithm based on maximum a posteriori and optimal transport. 基于 最大化后验及最优转换 利用这个分布进行后续的分类。

这篇文章是对n-way m-shot类MAML算法的改进。因算法中用到了无标签的测试数据集，故属于转导(transductive)学习。

转导推理（Transductive Inference）：是一种通过观察特定的训练样本，进而预测特定的测试样本的方法。从一个个例到另一个个例，实际案例直接结合过往的判例进行判决。
（传统的推理方法是归纳－演绎方法，人们首先根据用已有的信息定义一个一般规则，然后用这个规则来推断所需要的答案．也就是说，首先从特殊到一般，然后从一般到特殊．但是在转导模式中，我们进行直接的从特殊到特殊的推理，避免了推理中的不适定部分。）

模型概述如下：

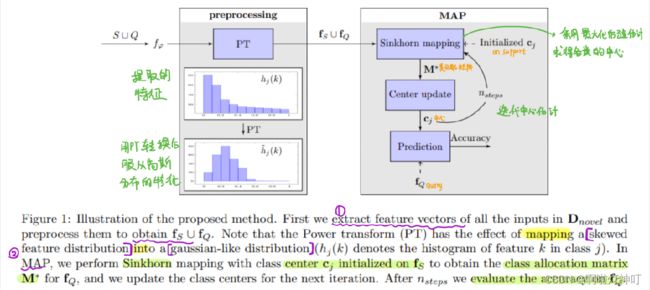
①Power Transform（PT）
算法提出对提取到的特征进行转换，使其更好地和后续算法假设的数据分布对齐。文章中使用了Power transform ，经过此变换可让任何分布的数据变换为服从close-to-Gaussian分布。
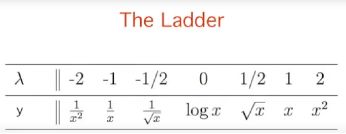
将得到的特征 v 进行幂变换，即

然后进行单位方差投影（除以它的模），即下面f(v)。
作用：
A. 通过调整 β 减少分布的skew，使之成为正态。
B. 单位方差投影将特征缩放到同一个尺度下，这样大方差特征也不会占据主导地位，这样预处理可以将任何数据映射到接近高斯分布的分布。

②MAP (Maximum A Posteriori Probability)
使用Sinkhorn算法在support set上初始化类中心cj，得到类分配矩阵，然后进行下一次更新。
更新n步之后在query上评估它的性能。

2.2.3 LaplacianShot

源于论文：Laplacian Regularized Few-Shot Learning（2020年）
发表在：发表：Proceedings of the 37 th International Conference on Machine Learning（CCF A类会议）
传送门：https://arxiv.org/pdf/2006.15486v1.pdf

本文为小样本提出了一个 拉普拉斯正则化推断，给定 从基类中学习到的特征嵌入，将 包含两个项的 二次二进制赋值函数 最小化：（下图）
①一个一元项，将query分配给最近的类原型
②一个成对的拉普拉斯项，距离相近的样本有一致的标签

Our transductive inference does not re-train the base model,and can be viewed as a graph clustering of the query set,subject to supervision constraints from the support set.
本文的转导推理不会重新训练基础模型，并且可以看作是query set的图聚类，受support set的监督约束。

We derive a computationally efficient bound optimizer of a relaxation of our function, which computes independent (parallel) updates for each query sample, while guaranteeing convergence. Following a simple cross-entropy training on the base classes, and without complex meta-learning strategies, we conducted comprehensive experiments over five fewshot learning benchmarks.
本文推导了一个计算效率很高的约束优化器，它在保证收敛性的同时，为每个查询样本计算独立（并行）更新。在基类上进行简单的交叉熵训练后，在没有复杂元学习策略的情况下，本文在五个fewshot学习基准上进行了综合实验。

公式：
本文提出了一种 转导小样本推理，它最小化 关于变量Y的 拉普拉斯正则化目标（受单纯形和整数约束）：
其中Y：C是类别个数，用0和1表示每一项

①第一项N（Y），当使用距离度量d（xq，mc），例如欧几里德距离，将每个查询点分配给支持集中最近的原型mc类时，第一项N（Y）得到全局最小化。
（在1-shot 中，类原型 mc 是support的类别，在 multi-shot中，类原型 mc 是support的平均值。）

②第二项L（Y），拉普拉斯正则化算子，其中亲和矩阵W=w(xq,xp)，用来评估特征向量 xq 和 xp 之间的相似性，并且可以使用一些核函数来计算。
拉普拉斯项鼓励 特征空间中 的邻近点（xq，xp）具有相同的潜在标签，从而对query进行正则化预测

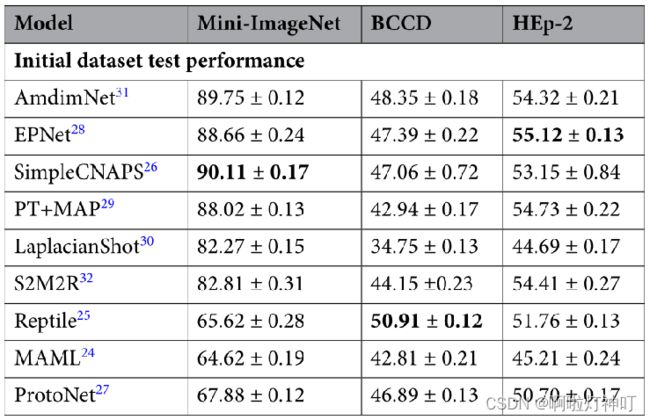
2.2.4 SimpleCNAPS

源于论文：CVPR2020_Improved Few-Shot Visual Classification
传送门：https://arxiv.org/pdf/1912.03432.pdf

特征提取部分：ResNet18+FiLM层（自适应任务）
最终分类：马氏距离（ Mahalanobis）

FiLM(Feature-wise Linear Modulation,FiLM)层：通过简单的特征仿射变换来影响神经网络计算。FiLM可以看作是条件归一化的泛化(A generalization of Conditional Normalization).学习以某方式在条件网络中选择特征,它还使CNN能够正确定位到Question所相关的对象.

马氏距离分类：通过求解协方差矩阵，去除各个分量之间的方差，消除了量纲性，并且加入的对数据分布的先验信息更少。

下图中，点代表embedded图像feature, 各个颜色交接处即为类决策边界，五角星代表query image。
左图：标准 L2-based距离，即欧式距离，
右图：马氏距离，基于类别协方差的距离度量
为了方便比较，本文把有图做了空间转换，即搞成了线性分割面。数据集：features: out-of-domain Traffic Signs dataset。该任务共包含五个类共112个support samples, 每个类一个query instance。
本文（右）的决策边界与support embedding对齐的更好，并且全都分类正确，基于L2的分类器有三类都分错了。

2.3 Augmented Metric-based 基于度量增强的方法

源于论文：Embedding Propagation: Smoother Manifold for Few-Shot Classification
传送门：https://arxiv.org/pdf/2003.04151.pdf

2.3.1 EPNet

产生背景：由于训练集和测试集的分布可能存在不同，产生的分布偏移（distribution shift）会导致较差的泛化性。流形平滑（Manifold smoothing）通过扩展决策边界和减少类别表示的噪音（extending the decision boundaries and reducing the noise of the class representations），已经被证明能够解决分布偏移问题。

idea：EPNet将 support set 和 query set 映射到一个嵌入空间，在该空间中，所有点都被同时考虑。在此阶段，标签从 support set 传播到未标记的 support set 。

下图是embedding propagation和label propagation的示意图，整个模型的inference流程如下：（a、b、c的注解在图中）
①输入一个episode
②通过特征提取器提取其特征
③对特征进行embedding propagation
④进行label propagation

embedding propagation 嵌入传播（下图）
①输入数据是由 feature extractor (CNN)得到的特征，通过以下的步骤得到输出表征：首先，对于每一对feature ，计算器 欧式距离d 以及邻接矩阵A，其中 σ 是比例系数，Aii =0 。
②计算对应的拉普拉斯矩阵L，其中D是度矩阵，是一个对角阵
③计算传播矩阵P，其中α是一个缩放参数，I是单位矩阵。
④最后得到embedding。最后得到的 z ̃ 可以看做是其邻居的带权和，该操作是很容易实现，同时其复杂度相对于对于小样本学习是可以忽略的。

Label propagation 标签传播
标签传播是半监督学习里的一项重要算法，这个算法的理论基础是“距离相近”的数据可能有着同样的标签。标签传播算法将所有的数据看作一张图，每一个数据点（不管是labeled还是unlabeled）都是一个个节点。
比如有如下9条数据，每个数据有两个feature，只有3个数据有label：

step1：
首先计算数据之间的“距离”，即权重矩阵中的权重值：

其中dij 是数据之间的欧氏距离，σ2 是一个权重参数。若i=j，那么wij =1，以此计算，得到一个9×9的权重矩阵W：

step2：
把这个权重矩阵转化为transition matrix T，用来表示数据之间标签转化的可能性，过渡矩阵T的初始定义为：

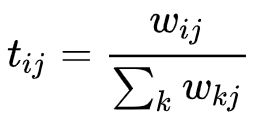
这个值÷这一列的和，相当于做了个归一化，得到T的大小也是9×9。

step3：
把标签y放在向量里，由于标签有3中，因此向量是3维的。初始化向量的规则如下：
A. 对于每一个数据，向量的各个维度加起来和为1。
B. 对于有label的数据，对应label那一维为1，其他维为0。
C. 对于无label的数据，所有的维度的值均相等。
由前面9条数据得到的初始标签矩阵Y为：

step4：
到目前为止，得到了三个矩阵：权重矩阵W（9×9），过渡矩阵T（9×9），标签矩阵Y（9×3）。
更新标签矩阵： Y <—— TY
向量的各个维度加起来的和，依旧是1。本来有标签的数据，依然是两个0一个1（one hot）。而本来没有标签的数据的的3个entry分别代表该数据隶属于该类别的可能性。

10次iteration之后结果如图：

基本每一个样本都有一个标签的概率超过50%，这时就可以开始assign标签了。当然这只是概率，必然不能保证标签100%的正确性，但在半监督环境下，标签传播算法能够帮助模型去合理地“假设”一个无标签的标签。标签传播算法收敛快慢和 σ 的选择有关。所以选择一个合理的 σ 很重要。

2.3.2 S2M2

源于论文：Charting the Right Manifold : Manifold Mixup for Few-shot Learning（2019.8.7）
传送门：https://arxiv.org/pdf/1907.12087v2.pdf

Db：基类；Dn：新类
第一阶段：在base dataset上训练一个（Nb-way的）分类器，在该阶段有两个损失，一个是分类损失classification loss，一个是额外损失auxiliary loss。
（额外损失来自于Manifold Mixup正则化 与 自监督损失（self-supervision task of rotation and exemplar））

第二阶段：冻结特征提取层，并根据Dn中k个随机抽样的新类的数据 训练一个新的（Nn-way）余弦分类器cWn，且使用分类损失

另外，Manifold Mixup是什么？
是对mixup数据增强算法的一种改进算法，把输入数据扩展到中间隐层进行混合，在数据传输到了中间第k层的时候进行mixup，输出混合后的融合向量与新的label。可视化如下：

mixup做了什么？
mixup邻域分布可以被理解为 一种数据增强方式，它令模型在处理 样本和样本之间 的区域时表现为线性。
我们认为，这种线性建模 减少了 在预测训练样本以外的数据时 的不适应性。
（实际上其操作的是向量）

Manifold Mixup论文链接：https://arxiv.org/pdf/1806.05236.pdf
mixup讲解：https://blog.csdn.net/u013841196/article/details/81049968

Manifold Mixup有什么优势？
①平滑决策边界
②拉大置信区间

2.3.3 AmDimNet（MAML的改进）

源于论文：题目：Self-supervised learning for few-shot image classification
传送门：https://arxiv.org/pdf/1911.06045.pdf
时间：2021.2.23

文章的主要的出发点在于将自监督学习引入小样本学习中，具体做法的是在将MAML中的全监督学习替换为自监督学习，以提高所提取特征的鲁棒性及泛化能力。

step1: Self-supervised learning stage

文章在第一步中将之前的全监督算法替换为了自监督算法。在小样本学习中因样本量较少，为防止过拟合，之前的文章大多采用较小的backbone，如resnet12等。而文章使用了自监督学习，可学到鲁棒性与泛化能力较强的特征，这降低了过拟合的可能性，故文章中采用了较大的backbone。

文章采用了AMDIM这一自监督学习算法，AMDIM算法的pretext是最大化同一个内容不同视角的最大交互信息。
(The pretext task is designed to maximize the mutual information between feature extracted from multiple views of a shared context. )

接着算法将最大化互信息下界问题转化为了最小化NCE(Noise Contrastive Esitimation，噪声对比估计)问题。

具体做法如题图stage-A中，对输入图像执行不同的数据增广操作，并在增广后的图像中选取不同的块作为局部特征，分别求全局a和局部b，全局b和局部a，局部a和局部b的互信息，得到最后的损失函数。

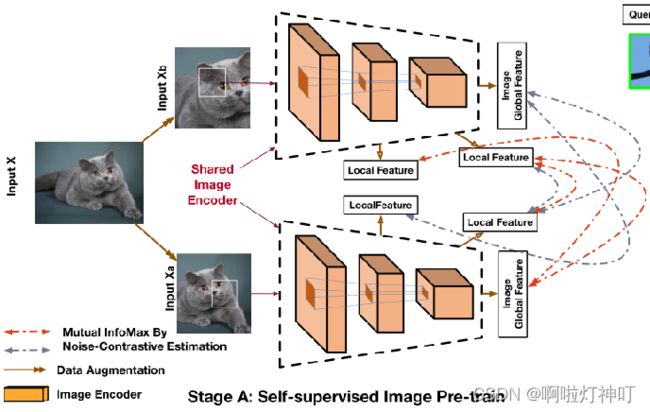
损失函数如下：

---

》》关于AmDimNet 》》》

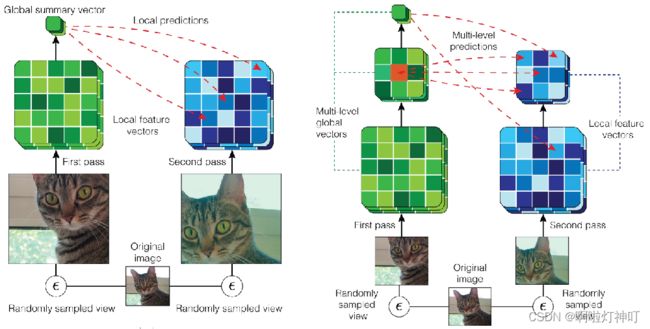
源于论文：Learning Representations by Maximizing Mutual Information Across Views
传送门：https://arxiv.org/pdf/1906.00910.pdf

左：Local DIM with predictions across views generated by data augmentation.（跨数据增强生成的视图）
右：Augmented Multiscale DIM, with multiscale infomax across views generated by data augmentation.（最大化多个尺度特征之间的互信息，考虑最大化 任意两个层的输出的 feature map 中，任意两个位置的图像块块之间的互信息）

---

step2: Meta-learning stage

文章没有采用全连接层来进行分类，而是对每个类学习了一个类中心，并采用一定的度量方式判断query与类中心的距离来进行分类。类中心的计算采用的是属于此类的样本的特征的均值，即属于某个类的特征总和，除以，样本个数：

距离采用的是欧氏距离，由样本到每个类的的距离可以判断样本属于每个类的概率，即这个样本与ck的距离，除以，与所有类的距离总和：

将support与query一起送到预训练的网络中，采用距离度量预测属于每个类的概率。如下图所示：