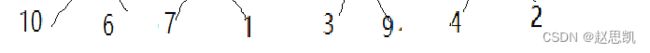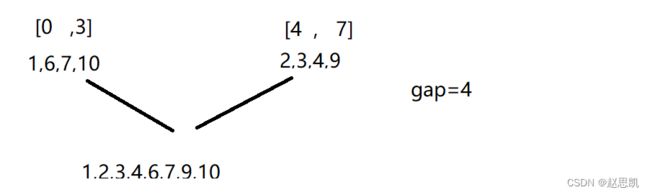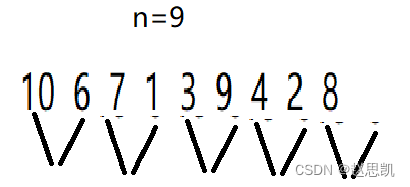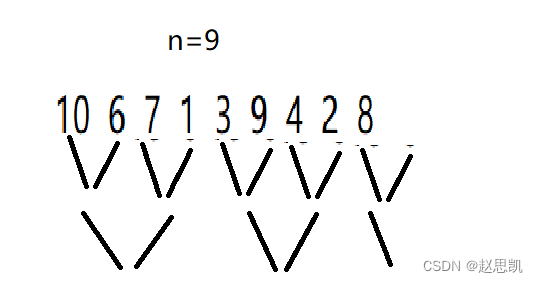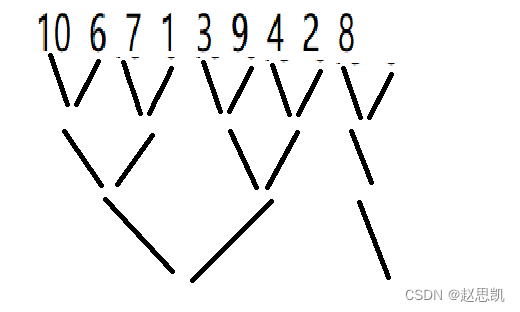2022_09_08__106期__排序

目录

目录

归并排序：

代码：

非递归归并排序：

计数排序的思想：

---

今天，我们引入一种新的排序方法：归并排序：

归并排序：

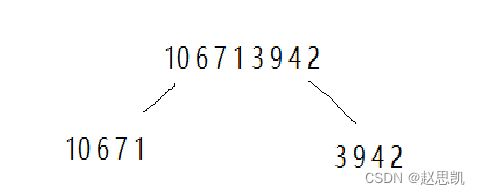
 假如对于这样一串数字，我们要对他进行从小到大的排序：

我们可以把它进行分化

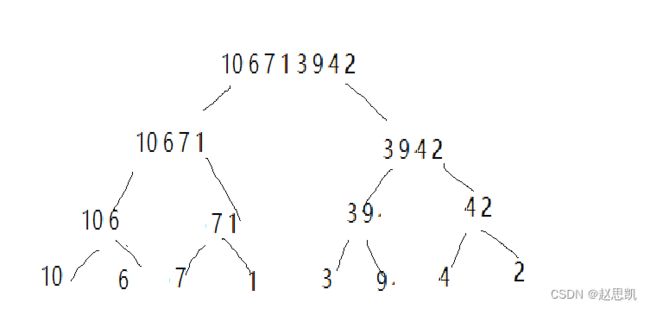
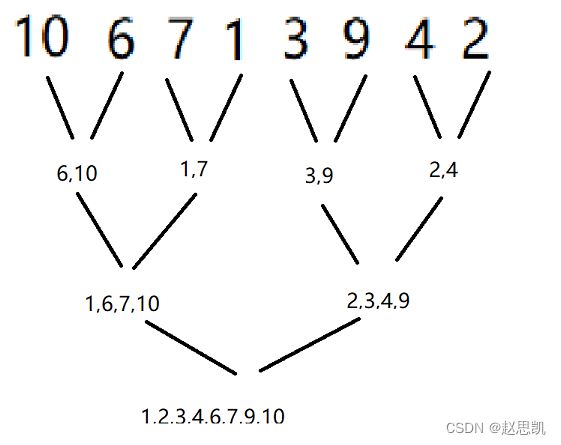
 再进行分化：

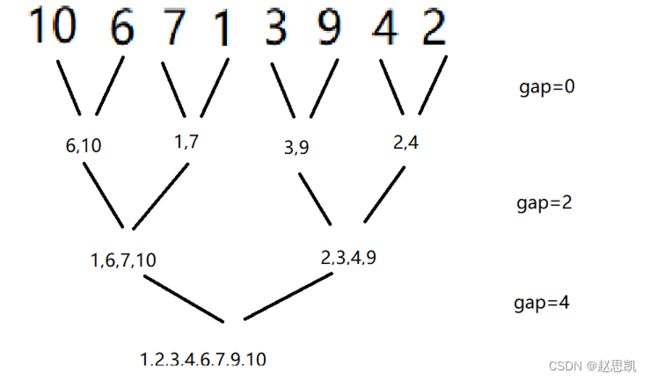
 我们将其逐步分化成为4组不同的数字，然后在组内，把大的元素进行尾插，实现在组内从小到大的排序，然后把对应的组数向上递归，然后再进行尾插，到最后实现从小到大的排序。

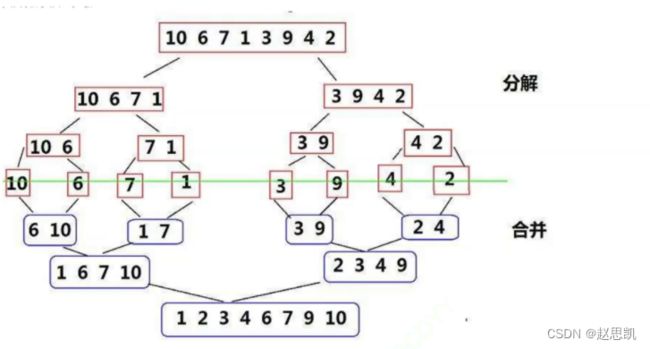
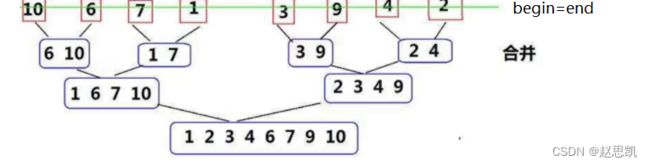
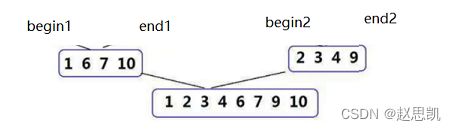
完整的实现思路如图所示：

 上面的上半部分表示的是分解，下半部分表示的是合并，最终合并成为从小到大的顺序。

我们进行分析：算法的时间复杂度是多少？

答：算法一共分为logN层，每一层都要计算N个数，所以算法的时间复杂度为O(N*logN）

代码：

void _MergeSort(int*a, int begin, int end, int*tmp)
{
	if (begin >= end)
	{
		return;
	}
	int mid = (begin + end) / 2;
	_MergeSort(a, 0, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);
	int begin1 = begin;
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = end;
	int i = begin;
	while (begin1 <= end1&&begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	while (a[begin1] <=a[end1])
	{
		tmp[i++] = a[begin1++];
	}
	while (a[begin2] <= a[end2])
	{
		tmp[i++] = a[begin2++];
	}
	memcpy(a + begin, tmp + begin, (end - begin + 1)*sizeof(int));
}
void MergeSort(int*a, int n)
{
	int*tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		return;
	}
	_MergeSort(a, 0, n - 1, tmp);
    free(tmp);
    tmp=NULL;
}

我们对代码进行分析：

int*tmp = (int*)malloc(sizeof(int)*n);

我们需要创建一个临时数组tmp，我们要把合并之后的数据存储到tmp中实现排序的目的，然后把临时数组tmp中的内存拷贝到我们的原数组中，从而实现排序。

我们的原数组有n个元素，类型为int，sizeof(int)表示int类型所占的字节数，n*sizeof(int)表示原数组所占空间的字节数，我们申请该大小的字节数，然后把其强制类型转化为整形指针，指向临时数组首元素的地址。

if (tmp == NULL)
	{
		return;
	}

我们先查看malloc返回值的定义：

 当这个函数申请内存失败的时候，我们会返回空指针，我们为了避免这种情况的发生，所以当malloc申请失败的时候，我们要退出程序。

_MergeSort(a, 0, n - 1, tmp);

对于如何实现数组的分解与合并，我们可以再写一个函数进行分析：

函数的参数：a表示要进行排序的数组名，0表示数组首元素的下标，n-1表示数组尾元素的下标，tmp表示我们要进行中转的临时数组。

free(tmp);
    tmp=NULL;

动态内存申请的空间，我们要进行释放，否则就会导致内存泄露。

free释放过内存空间时，我们要把对应的指针置为空，为了防止对该指针的误访问，我们要把该指针置为空。

接下来就是具体的操作部分：

if (begin >= end)
	{
		return;
	}

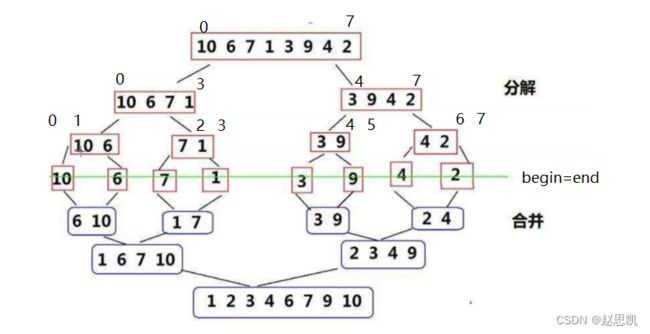
如图所示：

 我们可以发现，在绿线以上，都是begin小于end，当处于绿线部分时，表示begin=end，绿线部分表示数组已经被分解完毕，当begin大于end时的情况不会产生，所以当begin>=end时，我们要退出函数。

int mid = (begin + end) / 2;
	_MergeSort(a, 0, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);

 接下来，就是分解的主题部分，分解的方法我们采用递归，我们设置一个中间值mid，每次用mid把一个数组分割成为两个，我们通过调用两个分割后的函数实现递归。

当递归到最后一层时，表示我们已经对数据分割完毕，分割后的结果为：

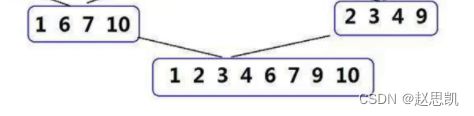
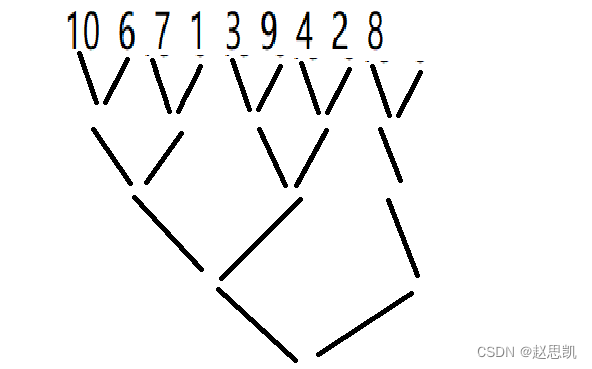
接下来，我们的目的是对这些数值进行归并，归并的过程如图所示：

 

 和递归的反过开及其相似，不同的是我们在归并的过程中还要实现排序。

int begin1 = begin;
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = end;
	int i = begin;
	while (begin1 <= end1&&begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	while (a[begin1] <=a[end1])
	{
		tmp[i++] = a[begin1++];
	}
	while (a[begin2] <= a[end2])
	{
		tmp[i++] = a[begin2++];
	}

当我们刚刚分解完毕时，我们的begin1为0，end1为0，begin2为1，end2为1

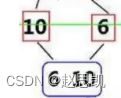
如图所示，我们要把10 和6操作成为 6 10 的形式：

 我们可以采取的思路是把小的6尾插入新数组，再把剩下的10插入到6的后面。

这是最开始的情况，最后的情况是这样：

 begin1为0，end1为3，begin2为4，end2为7

 我们的思路是让begin1和begin2对应的数比较大小，把小的进行尾插，假如begin1小的话，把begin1尾插到数组中，begin1++，数组下标++，再让begin1和begin2进行比较等等。

最终当begin1大于end1或者begin2大于end2时，我们只需要把剩余的元素进行尾插即可。

memcpy(a + begin, tmp + begin, (end - begin + 1)*sizeof(int));

最后，我们把tmp+begin处的内存拷贝到a+begin处，拷贝的字节数是end-begin+1个字节。

我们对代码进行编译：

非递归归并排序：

我们可以这样操作：

 

 我们可以通过创建参数gap来实现这个操作：

 对应的代码：

void MergeSortNonR(int*a, int n)
{
	int*tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	int gap = 1;
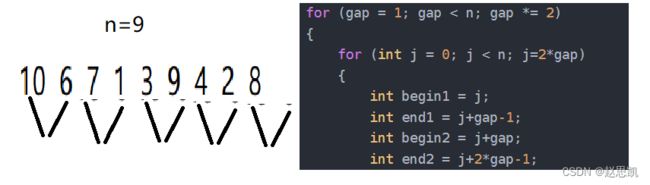
	for (gap = 1; gap < n; gap *= 2)
	{
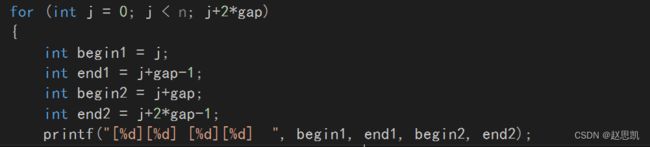
		for (int j = 0; j < n; j=2*gap)
		{
			int begin1 = j;
			int end1 = j+gap-1;
			int begin2 = j+gap;
			int end2 = j+2*gap-1;		
			while (begin1 <= end1&&begin2 <= end2)
			{
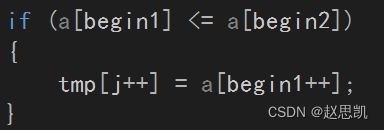
				if (a[begin1] <= a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
		}
	}
	free(tmp);
	tmp = NULL;
}

我们可以画图象进行解释：

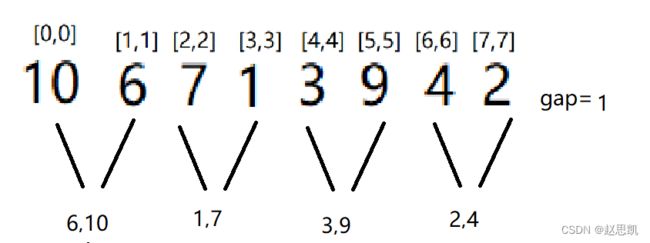
 gap等于0，表示我们要处理的数据的间距是0，我们每次归并的是两个这样的区间，所以处理当gap=0时，对应的处理结果为：

当gap为2时：

 其中，[]表示的是区间，也就是说，[0,1]代表的是前两个数字，所以我们处理完毕后的图象是：

当gap=4说，对应的图像：

 处理完毕的图象是：

 经过这些处理，我们数组中的数据实现归并排序

最后一步，我们要实现拷贝，实现拷贝的方法有两种：

第一种：每一轮拷贝一次：

void MergeSortNon(int*a, int n)
{
	int*tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	int gap = 1;
	for (gap = 1; gap < n; gap *= 2)
	{
		for (int j = 0; j < n; j=2*gap)
		{
			int begin1 = j;
			int end1 = j+gap-1;
			int begin2 = j+gap;
			int end2 = j+2*gap-1;		
			while (begin1 <= end1&&begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
		}
		memcpy(a, tmp, sizeof(int)*n);
	}
	free(tmp);
	tmp = NULL;
}

我们进行实验：

但是，这种方法也是不完整有缺陷的：例如：

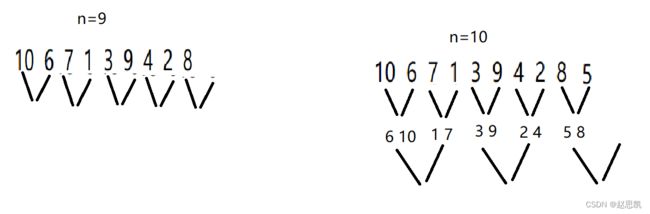
当我们要处理的数字并不是8个，而是9个甚至是10个时，对应的图像为：

当n=9时，第一轮gap=1时就会出现越界访问

当n=10时，第二轮gap=2时，也会出现越界访问。

我们编写代码进行尝试：

void MergeSortNonR(int*a, int n)
{
	int*tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	int gap = 1;
	for (gap = 1; gap < n; gap *= 2)
	{
		for (int j = 0; j < n; j+2*gap)
		{
			int begin1 = j;
			int end1 = j+gap-1;
			int begin2 = j+gap;
			int end2 = j+2*gap-1;		
			while (begin1 <= end1&&begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
		}
		memcpy(a, tmp, sizeof(int)*n);
	}
	free(tmp);
	tmp = NULL;
}
int main()
{
	int a[9] = { 10, 6, 7, 1, 3, 9, 4, 2,8};
	int n = sizeof(a) / sizeof(a[0]);
	MergeSortNonR(a, n);
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}

我们进行调试可以发现：

 触发了断点，一般触发了断电都是越界访问。

我们可以分析越界访问的位置：

 当第一次进入循环的末尾，当我们的j=8时，begin1=8，begin2=8+1=9

 a[begin2]造成越界访问。

我们先写一个代码检测有哪些越界：

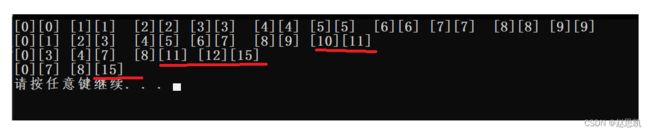
我们在这里打印出全部的begin和end，看看哪里越界了：

 

 由此看见，越界的情况有3种：

第一种：end1越界

第二种：end2越界

第三种：begin2和end2都越界。

不同的越界我们处理的方法是不同的，这时候，我们要处理的话，整体拷贝的难度就过大，所以我们使用局部拷贝的方法：

for (gap = 1; gap < n; gap *= 2)
	{
		for (int j = 0; j < n; j+2*gap)
		{
			int begin1 = j;
			int end1 = j+gap-1;
			int begin2 = j+gap;
			int end2 = j+2*gap-1;
			
			while (begin1 <= end1&&begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			printf("[%d][%d] [%d][%d]  ", begin1, end1, begin2, end2);
			memcpy(a + j, tmp + j, (end2 - j + 1));
		}
		printf("\n");

不同越界的不同处理方法：

1：我们首先画不同越界对应的图像：

end1越界：

 我们可以这样处理：

 我们进行分析，因为我们的拷贝是局部拷贝，所以当我们的end1>=n的时候，我们的前8个数据已经被拷贝完毕。

我们break退出，这时候我们对应的图象是：

 这时候的end2依旧大于等于n

 end2还是大于等于n

 这时候，end1满足条件，我们归下来。

end2越界：

当end2越界时，我们只需要把end2置为n-1，也就是最后一个元素对应的下标，即可。

begin2和end2都越界时：

直接break；

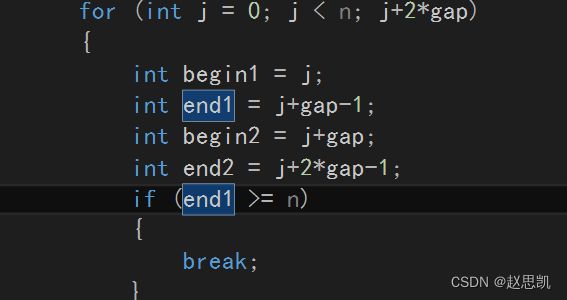
当我们添加完所有的限制条件：

void MergeSortNonR(int*a, int n)
{
	int*tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	int gap = 1;
	while (gap= n)
			{
				break;
			}
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			if (begin2 >= n)
			{
				break;
			}
			while (begin1 <= end1&&begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[i++] = a[begin1++];
				}
				else
				{
					tmp[i++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[i++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[i++] = a[begin2++];
			}
			memcpy(a + j, tmp + j, (end2 - j + 1)*sizeof(int));
		}
		/*memcpy(a, tmp, sizeof(int)*n);*/
		gap *= 2;
	}
	free(tmp);
	tmp = NULL;
}
int main()
{
	int arr[9] = { 10, 6, 7, 1, 3, 9, 4, 2,8};
	int n = sizeof(arr) / sizeof(arr[0]);
	MergeSortNonR(arr, n);
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;
}

我们进行编译：

         

计数排序的思想：

假如对于这样一串数字：

 我们可以采取计数的方式来排序：

我们有七个数的话，开辟八个整型空间，全部初始化为0.

 我们把数组从前往后遍历，出现哪一个数字，这个数字对应的下标中的数字+1

例如，我们的3出现了两次，3对应的下标所对应的数值+2：

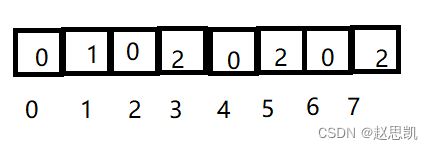
 所以经过我们的操作：

 通过这个计数的方法：我们可以排除这一串数组对应的顺序：

1，3，3，5，5，7，7

其他的情况：

假如我们要排序的是这样的一串数字

 那我们还要从0开始创建吗，那我们就需要创建106个空间，空间浪费就太严重了，我们可以采取相对映射的方法

相对映射：开辟max-min+1个空间，对于这里，我们可以开辟21个空间。

映射的相对位置就是：a[i]-min.例如105映射的相对位置就是105-100=5.

相对映射对于负数也同样管用：

例如这样的一串数字：

-11，-12，-13，-14，-15.

我们要开辟max-min-1个空间，也就是-11+15+1也就是5个空间。

他们映射的相对位置分别是：4，3，2，1，0.

映射对浮点数不适用。

计数排序的实现：

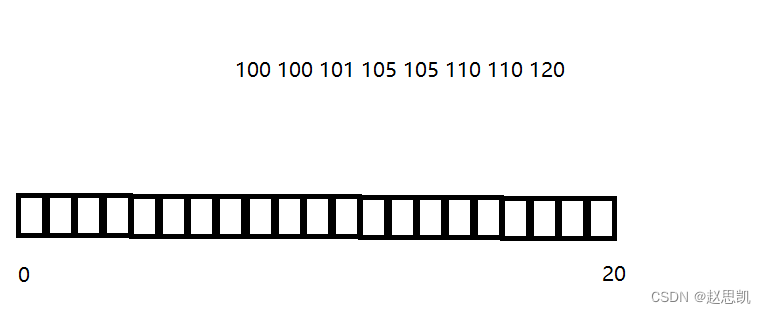
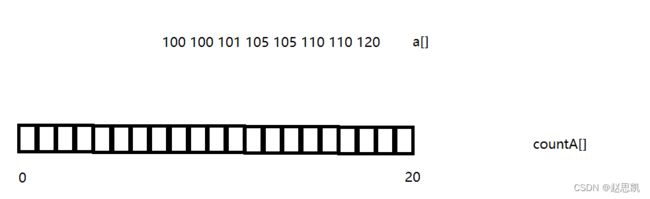
对于如图所示的数，我们进行排序：

我们首先要求出数组中最小的数和最大的数

最小的数为100，最大的数为120.

我们需要额外开辟空间用来计数：我们需要额外开辟max-min+1也就是21个空间。

 

 

100出现两次，我们的countA[0]就加2.

所以countA[a[i]-min]代表出现的次数。

然后我们根据countA[]数组中的值来对数组进行排序。

计数排序的代码：

#include

void CountSort(int*a, int n)
{
	int max = a[0];
	int min = a[0];
	for (int i = 1; i < n; i++)
	{
		if (a[i]>max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}
	int range = max - min + 1;
	int*countA = (int*)malloc(sizeof(int)*range);
	if (countA == NULL)
	{
		perror("malloc fail");
		return;
	}
	memset(countA, 0, sizeof(int)*range);
	for (int i = 0; i < n;i++)
	{
		countA[a[i] - min]++;
	}
	int j = 0;
	for (int i = 0; i < range; ++i)
	{
		while (countA[i]--)
		{
			a[j] = i + min;
			++j;
		}
	}
}

我们对代码进行分析：

计数排序主要分为以下这些步骤：

首先，就是求数组中的最大数和最小数，我们采取的方法是类似冒泡的写法，但是注意我们这里的max和min一定要初始化为a[0]，假如我们初始化为0时，假如我们的数字全是复数，那么我们求的最大值就是0了，但是0并不属于这个数组。

求出最大数和最小数，套用公式max-min+1表示我们计数数组的元素个数。

我们通过元素个数额外开辟一个数组countA，数组有max-min+1个元素。

我们使用memset把数组countA全部初始化为0，因为我们的数组的数据表示数组a对应元素的个数。

接下来，我们根据数组a的元素内容，对数组countA进行填充。

填充的方法如下，a[i]-min表示数组a在countA中的映射下标。我们通过i值的改变来使countA[a[i]-min]的值发生变化。

我们的countA数组中的内容已经初始化完毕了，我们要通过countA数组中的内容对数组a进行排序。

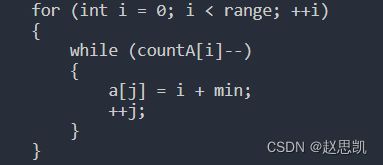
for循环表示我们要把countA数组的全部内容进行遍历。

countA[i]--表示循环i次，i+min则对应数组a中的值。我们根据循环的次数对数组a进行初始化从而实现排序。

我们进行检测：