AHP层次分析法
AHP层次分析法
1. 介绍
层次分析法(analytic hierarchy process, AHP)适用于结构较为复杂、决策准则较多而且不易量化的决策问题。
其思路是紧密地和决策者的主观判断和推理联系起来,对决策者的推理过程进行量化的描述,可以避免决策者在结构复杂和方案较多时逻辑推理上失误。
层次分析法的基本内容是:
- 根据问题的性质和要求,提出一个总的目标;
- 将问题按层次分解,对同一层次内的诸因素通过两两比较的方法确定出相对于上一层目标的各自权系数;
- 层层分析下去,直到最后一层给出所有因素或者方案相对于总目标而言的按重要性(或偏好)程度的一个排序。
2. 具体步骤
- 明确问题,提出总目标。
- 建立层次结构,把问题分解成若干层次。第一层为目标层(总目标),中间层可分为准则层(目标层)和子准则层(部门层)等,最低层一般为方案层(措施层)。
- 求同一层次上的权系数(从高层到低层)。
- 求同一层次上的组合权系数。
- 一致性检验。
–
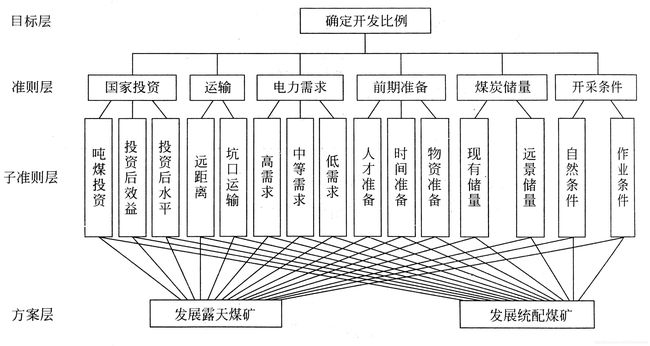
第二步中,可建立如下分层结构图:
第三步中,假设当前层次上的因素为 A 1 , ⋯ , A n A_1,\cdots,A_n A1,⋯,An,相关的上一层因素为 C C C,则可针对因素 C C C,对所有因素 A 1 , ⋯ , A n A_1,\cdots,A_n A1,⋯,An进行两两比较得到数值 a i j a_{ij} aij,数值定义如下:
| 相对重要程度a_ij | 定义 | 解释 |
|---|---|---|
| 1 | 同等重要 | 目标i和j同样重要 |
| 3 | 略微重要 | 目标i比目标j略微重要 |
| 5 | 相当重要 | 目标i比目标j重要 |
| 7 | 明显重要 | 目标i比目标j明显重要 |
| 9 | 绝对重要 | 目标i比目标j绝对重要 |
| 2,4,6,8 | 介于两相邻重要程度之间 |
一些符号定义:
A = ( a i j ) n × n \pmb{A}=(a_{ij})_{n \times n} AAA=(aij)n×n:因素 A 1 , ⋯ , A n A_1,\cdots,A_n A1,⋯,An相应于上一层因素 C C C的判断矩阵。
λ m a x \lambda_{max} λmax: A A A的最大特征根。
w = ( w 1 , ⋯ , w n ) T \pmb{w}=(w_1,\cdots,w_n)^T www=(w1,⋯,wn)T:属于 λ m a x \lambda_{max} λmax的标准化的特征向量。
第四步中,设当前层次上的因素为 A 1 , ⋯ , A n A_1,\cdots,A_n A1,⋯,An,相关的上一层因素为 C 1 , ⋯ , C m C_1,\cdots,C_m C1,⋯,Cm,则对每个 C i C_i Ci,可得一个权向量 w i = ( w 1 i , ⋯ , w n i ) T \pmb{w}^i=(w_1^i,\cdots,w_n^i)^T wwwi=(w1i,⋯,wni)T,如果已知上一层 m m m个因素的权重分别为 a 1 , ⋯ , a m a_1, \cdots, a_m a1,⋯,am,则当前层每个因素的组合权系数为:
∑ i = 1 m a i w 1 i , ∑ i = 1 m a i w 2 i , ⋯ , ∑ i = 1 m a i w n i \sum^m_{i=1}a_iw^i_1, \sum^m_{i=1}a_iw^i_2,\cdots,\sum^m_{i=1}a_iw^i_n i=1∑maiw1i,i=1∑maiw2i,⋯,i=1∑maiwni
由上式可知,若记 B k B_k Bk为第 k k k层次上的所有因素相对于上一层上有关因素的权向量按列组成的矩阵,则第 k k k层次的组合权系数向量 W k W^k Wk满足:
W k = B k ⋅ B k − 1 ⋯ B 2 ⋅ B 1 W^k=B_k\cdot B_{k-1}\cdots B_2\cdot B_1 Wk=Bk⋅Bk−1⋯B2⋅B1
其中 B 1 = ( 1 ) B_1=(1) B1=(1)
第五步中,在得到判断矩阵A时,有时免不了会出现判断上的不一致性,因而需要利用一致性指标来进行检验。作为度量判断矩阵偏离一致性的指标,可以用
C I = λ m a x − n n − 1 CI=\frac{\lambda_{max}-n}{n-1} CI=n−1λmax−n
来检查决策者判断思维的一致性。为了度量不同的判断矩阵是否具有满意的一致性,还需要利用判断矩阵的平均随机一致性指标RI。对于1阶到9阶的判断矩阵,RI的值分别为:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
| 0.00 | 0.00 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
判断矩阵的一致性指标CI与同阶平均随机一致性指标RI相比,称为随机一致性比率,记为:
C R = C I R I CR=\frac{CI}{RI} CR=RICI
通常要求 C R ≤ 0.1 CR\leq0.1 CR≤0.1,此时可以认为判断矩阵具有满意的一致性,否则需要对判断矩阵进行调整。
3. 方根法与和积法
3.1 方根法
第一步,计算 w ‾ i \overline{w}_i wi,其中
w ‾ i = Π j = 1 n a i j n \overline{w}_i=\sqrt[n]{\Pi^n_{j=1}a_{ij}} wi=nΠj=1naij
第二步,将 w ‾ i \overline{w}_i wi规范化,得到 w i w_i wi
w i = w ‾ i ∑ i = 1 n w ‾ i w_i=\frac{\overline{w}_i}{\sum^n_{i=1}\overline{w}_i} wi=∑i=1nwiwi
其中, i = 1 , 2 , ⋯ , n i=1,2,\cdots,n i=1,2,⋯,n
第三步,求 λ m a x \lambda_{max} λmax
λ m a x = ∑ i = 1 n ∑ j = 1 n a i j w j n w i \lambda_{max}=\sum^n_{i=1}\frac{\sum^n_{j=1}a_{ij}w_{j}}{nw_i} λmax=i=1∑nnwi∑j=1naijwj
3.2 和积法
第一步,按列将 A \pmb{A} AAA规范化
b ‾ i j = a i j ∑ k = 1 n a k j \overline{b}_{ij}=\frac{a_{ij}}{\sum^n_{k=1}a_{kj}} bij=∑k=1nakjaij
第二步, 计算 w ‾ i \overline{w}_i wi
w ‾ i = ∑ j = 1 n b ‾ i j \overline{w}_i=\sum^n_{j=1}\overline{b}_{ij} wi=j=1∑nbij
第三步, 将 w ‾ i \overline{w}_i wi规范化,得到 w i w_i wi
w i = w ‾ i ∑ i = 1 n w ‾ i w_i=\frac{\overline{w}_i}{\sum^n_{i=1}\overline{w}_i} wi=∑i=1nwiwi
其中, i = 1 , 2 , ⋯ , n i=1,2,\cdots,n i=1,2,⋯,n
w i w_i wi即特征向量 w w w的第 i i i个分量。
第四步, 计算 λ m a x \lambda_{max} λmax
λ m a x = ∑ i = 1 n ∑ j = 1 n a i j w j n w i \lambda_{max}=\sum^n_{i=1}\frac{\sum^n_{j=1}a_{ij}w_{j}}{nw_i} λmax=i=1∑nnwi∑j=1naijwj
4. 代码示例
import numpy as np
# RI
RI=[0.0,0.0,0.58,0.9,1.12,1.24,1.32,1.41,1.45]
# 第一准则层
A = np.array([1, 1, 1, 4, 1, 1/2,
1, 1, 2, 4, 1, 1/2,
1, 1/2, 1, 5, 3, 1/2,
1/4, 1/4, 1/5, 1, 1/3, 1/3,
1, 1, 1/3, 3, 1, 1,
2, 2, 2, 3, 1, 1]).reshape([6, 6])
# 方案层
B1 = np.array([1, 1/4, 1/2, 4, 1, 3, 2, 1/3, 1]).reshape([3, 3])
B2 = np.array([1, 1/4, 1/5, 4, 1, 1/2, 5, 2, 1]).reshape([3, 3])
B3 = np.array([1, 3, 1/3, 1/3, 1, 1, 3, 1, 1]).reshape([3, 3])
B4 = np.array([1, 1/3, 5, 3, 1, 7, 1/5, 1/7, 1]).reshape([3, 3])
B5 = np.array([1, 1, 7, 1, 1, 7, 1/7, 1/7, 1]).reshape([3, 3])
B6 = np.array([1, 7, 9, 1/7, 1, 5, 1/9, 1/5, 1]).reshape([3, 3])
class lam_w:
def __init__(self, listw, lambda_max):
self.listw = listw
self.lambda_max = lambda_max
# 方根法
def lambdafunc(matrix):
# 计算w_hat
w_hat=[]
a_prod=1
for i in range(matrix.shape[0]):
for a in matrix[i]:
a_prod *= a
w_hat.append(pow(a_prod,1/matrix.shape[0]))
a_prod=1
# print("w_hat:",w_hat)
# 规范化
w=[]
w_sum=0
for wi in w_hat:
w_sum += wi
for wi in w_hat:
w.append(wi/w_sum)
w = np.array(w) # 转化为数组
# 求lambda
aw=[]
aw_ij=0
lambda_max=0
for i in range(matrix.shape[0]):
for j in range(matrix.shape[1]):
aw_ij += matrix[i][j]*w[j]
aw.append(aw_ij/matrix.shape[0]/w[i])
aw_ij=0
for k in range(len(aw)):
lambda_max += aw[k]
# print("\nlambda:",lambda_max)
# 判断CR
CI = (lambda_max-matrix.shape[0])/(matrix.shape[0]-1)
CR = CI/RI[matrix.shape[0]-1]
if CR<0.1:
print("Success! and the CR is ", round(CR,4))
else:
print("Wrong! because the CR is ", round(CR,4))
# output
result = lam_w(w, lambda_max)
# print(result.listw)
return result
if __name__ == '__main__':
a = lambdafunc(A)
b1 = lambdafunc(B1)
b2 = lambdafunc(B2)
b3 = lambdafunc(B3)
b4 = lambdafunc(B4)
b5 = lambdafunc(B5)
b6 = lambdafunc(B6)
b = np.vstack((b1.listw, b2.listw, b3.listw, b4.listw, b5.listw, b6.listw))
b = b.T
resultlist = b.dot(a.listw.T)
list = np.argsort(resultlist)
print("Best person's order: ",list[-1]+1)