深度学习—卷积神经网络AlexNet
卷积神经网络AlexNet
- 1. AlexNet的历史
- 2. AlexNet网络结构简要分析
- 3. AlexNet的改进
- 4. 结尾
- 参考资料
在这一讲中,我们将详细讲解深度学习发展中的重要里程碑AlexNet。
1. AlexNet的历史
2012年Geoffrey Hintton的学生ALEX Krizhevsky构建了一个包含65万多个神经元,待估计参数超过6000万的大规模的卷积神经网络。他以自己的名字命名了这个神经网络叫作AlexNet,用以解决ImageNet数据集1000类的分类问题。在2012年,ImageNet测试比赛上取得了远超Goole和Facebook两个大公司的成绩。相比前面讲过的LeNet,AlexNet在网络结构上深了很多,即神经网络层数和每层神经元个数多了很多,但其基本思想与LeNet完全一样,我们看懂了LeNet后能很容易看懂AlexNet,下图1是AlexNet的网络结构图。
2. AlexNet网络结构简要分析
从图1也可以看到,它也是由一些卷积层、降采样层和全连接层组成的。需要注意的是层与层之间也有非线性函数和Batch Normalization,图中没有画出。下面举例说明AlexNet的网络结构。
例如在图中第一个卷积层中,输入的是227×227的彩色图片,由于彩色图片有RGB三个颜色分量,所以channel数量为3。第一个卷积层有96个11×11×3的卷积核,卷积的步长stride=(4,4)。
根据上一讲的思考题,如果一个M×N的图像和一个m×n的卷积核进行操作,移动步长stride=(P,Q),即在长的方向上每步移动P个像素,在宽这个方向上每步移动Q个像素,请问经过卷积操作后获得的特征图的长H和宽W分别是多少呢?
H = f l o o r ( M − m P ) + 1 H=floor(\frac{M-m}{P})+1 H=floor(PM−m)+1
W = f l o o r ( N − n Q ) + 1 W=floor(\frac{N-n}{Q})+1 W=floor(QN−n)+1
代入计算可以得出,第一个卷积层获得的特征图长宽都是55,由于有96个卷积核,因此特征图的通道数即channel数量为96。基于类似的方法大家可以自行分析一下AlexNet其它层的结构参数,从而看懂整个网络的结构。
3. AlexNet的改进
AlexNet相比LeNet有以下方面的改进:
(1)第一个改进以ReLu函数代替LeNet中的Sigmoid或tanh函数。
R e L u ( x ) = m a x ( 0 , x ) ReLu(x)=max(0,x) ReLu(x)=max(0,x)

前面讲到Sigmoid和tanh在绝对值较大的时候会出现梯度消失现象,这对层数很深的深度网络的收敛是不利的,ReLu函数的全称是Rectified Linear Units,其函数表达式如下
f ( x ) = { 0 , x < 0 x , x > 0 f(x)= \left \{\begin{array}{cc} 0, &x <0\\ x, &x>0 \end{array}\right. f(x)={0,x,x<0x>0
其导数表达式是如下
f ′ ( x ) = { 0 , x < 0 1 , x > 0 f'(x)= \left \{\begin{array}{cc} 0, &x <0\\ 1, &x>0 \end{array}\right. f′(x)={0,1,x<0x>0
这样在自变量 x > 0 x>0 x>0时,上一层的梯度就能够直接传到下一层,避免了梯度消失的现象。
另一方面,ReLu函数把自变量 x < 0 x<0 x<0时的函数值设置为0,假设某一层的神经元输出大于0和小于0的个数差不多,那么利用ReLu函数可以关闭一半左右的神经元,使它们处于非激活状态。因此ReLu函数保证了每一次网络中只有很少一部分神经元的参数被更新,这样做可以促进深度神经网络的收敛。这就像一个庞大社会,如果每一个人都标新立异,那么社会的结构往往是不稳定的,但如果大多数人兢兢业业,而少部分人标新立异,那么社会结构在稳定的同时也会具有创造性。
(2)第二个改进是降采样层Maxpooling代替LeNet的平均降采样
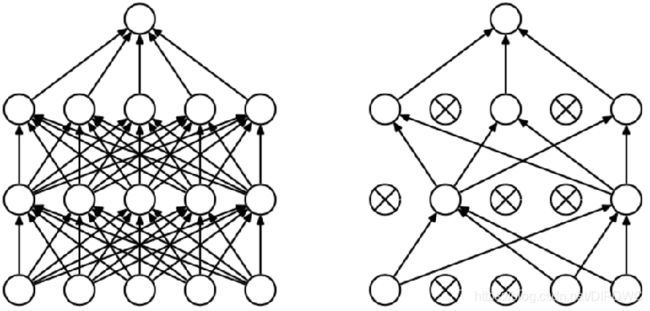
ALEX为降采样操作取了一个新的名字叫池化(Pooling),把邻近的像素作为一个“池子”来重新考虑,如下图所示。

图中左边所有红色像素值可以看做一个池子,经过池化操作过后变成右边一个浅蓝色的像素。
ALEX提出了 最大池化(Maxpooling) 的概念,对每一个邻近的像素组成的池子,选取最大值作为输出。相比平均池化(Average Pooling),最大池化(Maxpooling) 之所以能够促进网络的收敛,其原因与ReLu函数是类似的,在最大池化下,梯度直接传导到最大值,而不是平均分配到池子里面的每个元素,这样每次更新的参数将会进一步减少,从而保证了网络的稳定性。
(3)第三个改进是随机丢弃(Dropout)
为了避免系统参数更新过快导致过拟合。ALEX每次利用训练样本更新参数的时候,随机的“丢弃” 一定比例的神经元,被丢弃的神经元将不参加训练过程,输入和输出该神经元的权重系数也不做更新。这样每次训练时,训练的网络结构都不一样,而这些不同的网络结构却分享共同的权重系数。
随机丢弃(Dropout)的做法是对每一层每次训练时以概率P丢弃一些神经元。下图中画出了Dropout概率p=0.5时的情况,Dropout技术减缓了网络收敛速度,也以大概率避免了过拟合现象的发生。
(4)第四个改进是数据扩增(Data Augumentation)
数据扩增(Data Augumentation)增加训练样本,尽管2012年ImageNet的训练样本数量有超过120万幅图像,但是相对于如此巨大的网络结构来说,训练图像仍然是不够的。ALEX等人采用了多种方法增加训练样本,包括:
- 将原图像翻转
- 将
256×256的图像随机选取224×224的片段做为输入图像
运用上面两种方法的组合,可以将一幅图像变为2048幅图像,同时还可以对每幅图像引入一定的噪声,构成新的图像,这样做可以较大规模增加训练样本,避免由于训练样本不够造成的性能损失。数据扩增(Data Augumentation) 目前被广泛应用于深度模型训练中。
(4)第五个改进是用GPU加速训练过程
采用了2片GTX 580 GPU,对训练过程进行加速。由于GPU强大的并行计算能力,使得训练过程的时间缩短了数10倍,哪怕是这样,训练的时间仍然持续了6天。在2013年最初的论文中,AlexNet结构如下图所示。

同我们的前面的结构示意图相比,这张图是完全一样的,只是作者将每一层的特征图的通道(channels)平均分成两份,分别画在上面和下面。这样画是因为作者使用了2块GPU,所以一块GPU管理上面的运算,另一块GPU管理下面的运算。
GPU(Graphic Processing Unit) 有一个通俗的中文名字叫作显卡,它是一种专门在个人电脑、工作站、游戏机和一些移动设备上图像运算工作的微处理器。它的特点是线性计算并行化的程度好,这个特点正好被ALEX Krizhevsky用来做神经网络传播的梯度更新。
利用GPU进行深度学习训练这一重要改进使专门生产GPU的公司,如美国的NVIDIA公司变得炙手可热,从2015年开始NVIDIA的股票持续上涨,到目前股票增值了将近20倍。近年来,GPU性能在不断增强以及GPU相关的软件也不断的发展,相比2012年ALEX Krizhevsky最初利用GPU训练时期早已不可同日语。目前,利用2万元左右的GPU设备重复ALEX Krizhevsky在2012年的实验只需要几个小时。
4. 结尾
这一节我们详细介绍了AlexNet的结构以及AlexNet对于卷积神经网络的一系列改进,它们分别是:
- Relu函数
- 最大池化(
Maxpooling) - 随机丢弃(
Dropout) - 数据扩增(
Data Augumentation) - 用GPU加速训练深度神经网络
目前,这些改进已经被公认为训练深度神经网络的重要方法,在不同的深度神经网络的训练上获得一系列的应用。
本讲的最后有一道思考题:
我们前面详细计算了LeNet的待估计参数个数,如下图所示。
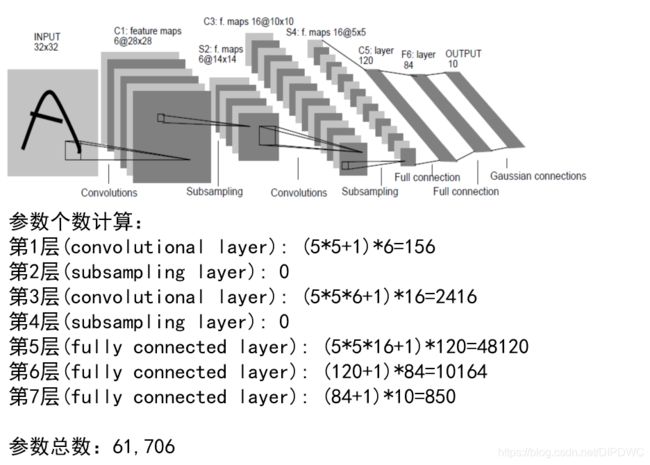
请你根据这一讲提到的AlexNet的网络结构图,也计算一下每层参数的个数。
参考资料
- 浙江大学《机器学习》课程—胡浩基老师主讲
- A. Krizhevsky, I. Sutskever and G. E. Hinton. ImageNet Classification with Deep Convolutional Neural Networks. Advances in Neural Information Processing 25, MIT Press, Cambridge, MA, 2012.
- LeCun Y., Bottou L., Bengio Y., and Haffner P., Gradient-based learning applied to document recognition, Proceedings of the IEEE, pp. 1-7, 1998.
如果文章对你有帮助,请记得点赞与关注,谢谢!
![]()