国赛数模2017B思路汇总第一部分（题目一）
前言
笔者是在读本科生，尝试复刻数模国赛2017B题后，对国家一等奖论文做出总结，并说出自己的一些想法，以图提高自身建模水平。
原题
B题 “拍照赚钱”的任务定价
“拍照赚钱”是移动互联网下的一种自助式服务模式。用户下载APP，注册成为APP的会员，然后从APP上领取需要拍照的任务（比如上超市去检查某种商品的上架情况），赚取APP对任务所标定的酬金。这种基于移动互联网的自助式劳务众包平台，为企业提供各种商业检查和信息搜集，相比传统的市场调查方式可以大大节省调查成本，而且有效地保证了调查数据真实性，缩短了调查的周期。因此APP成为该平台运行的核心，而APP中的任务定价又是其核心要素。如果定价不合理，有的任务就会无人问津，而导致商品检查的失败。
附件一是一个已结束项目的任务数据，包含了每个任务的位置、定价和完成情况（“1”表示完成，“0”表示未完成）；附件二是会员信息数据，包含了会员的位置、信誉值、参考其信誉给出的任务开始预订时间和预订限额，原则上会员信誉越高，越优先开始挑选任务，其配额也就越大（任务分配时实际上是根据预订限额所占比例进行配发）；附件三是一个新的检查项目任务数据，只有任务的位置信息。请完成下面的问题：
1.研究附件一中项目的任务定价规律，分析任务未完成的原因。
2.为附件一中的项目设计新的任务定价方案，并和原方案进行比较。
3.实际情况下，多个任务可能因为位置比较集中，导致用户会争相选择，一种考虑是将这些任务联合在一起打包发布。在这种考虑下，如何修改前面的定价模型，对最终的任务完成情况又有什么影响？
4.对附件三中的新项目给出你的任务定价方案，并评价该方案的实施效果。
附件一：已结束项目任务数据
附件二：会员信息数据
附件三：新项目任务数据
题目一
1、聚类法
（1）k均值法+多元线性回归（B104）
（1）先绘制散点图，发现多数会员位于广东省内，因此排除广东省外的少数数据。
（2）用k均值聚类将会员分为三个大类（大体上是广佛，东莞，深圳），找出聚类中心。
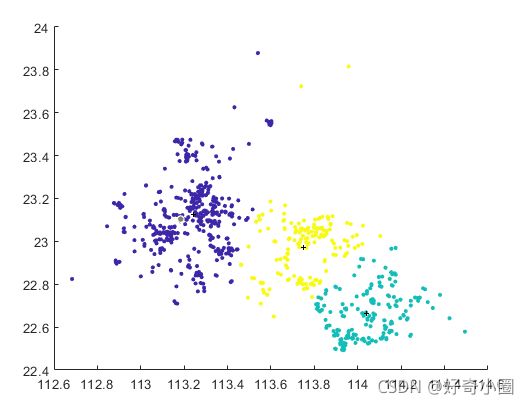
（3）设定指标“偏僻程度”、“会员密度”、“任务密度”三个指标，并进行标准化
z 1 = ∣ P i O j ∣ ∣ P m O j ∣ = ( x i 2 − x j 2 ) + ( y i 2 − y j 2 ) ( x m 2 − x j 2 ) + ( y m 2 − y j 2 ) z_{1}=\frac{\left|P_{i} O_{j}\right|}{\left|P_{m} O_{j}\right|}=\frac{\sqrt{\left(x_{i}^{2}-x_{j}^{2}\right)+\left(y_{i}^{2}-y_{j}^{2}\right)}}{\sqrt{\left(x_{m}^{2}-x_{j}^{2}\right)+\left(y_{m}^{2}-y_{j}^{2}\right)}} z1=∣PmOj∣∣PiOj∣=(xm2−xj2)+(ym2−yj2)(xi2−xj2)+(yi2−yj2)
记 z 2 z_{2} z2 为会员密度。
z 2 = n m − n i n m z_{2}=\frac{n_{m}-n_{i}}{n_{m}} z2=nmnm−ni
n i n_{\mathrm{i}} ni 为任务点 1.5 k m 1.5 \mathrm{~km} 1.5 km 圆域内的会员数量, n m n_{\mathrm{m}} nm 是 n i n_{\mathrm{i}} ni 的最大值。
记 z 3 z_{3} z3 为任务密度。
z 3 = m m − m i m m z_{3}=\frac{m_{m}-m_{i}}{m_{m}} z3=mmmm−mi
（4）然后根据已有的定价数据对这三个自变量进行拟合，即可得到定价公式。
w = 8.2233 z 1 − 0.1959 z 2 + 3.7487 z 3 + 65 w=8.2233 z_{1}-0.1959 z_{2}+3.7487 z_{3}+65 w=8.2233z1−0.1959z2+3.7487z3+65
（2）FCM地理中心聚类+一元函数（B353）
相比K均值聚类，这种方法显得更加专业
（1）通过调用 MATLAB 函数中[center, U, obj_fcn] = FCM(data, cluster_n, options)语句实现FCM聚类。
（2）Options 中, 隶属度矩阵 U \mathrm{U} U 的指数设为 3.0 3.0 3.0; 最大迭代次数设为 50 次, 迭代待终止条件为隶属度最小变化量小于 1 e − 5 1 \mathrm{e}-5 1e−5.
（3）根据聚类中心，对距离和定价进行一元线性拟合 f ( x ) = a x + b f(x)=a x+b f(x)=ax+b，即可得到对应每个聚类中心的线性函数。
（4）进行聚类有效性分析，本文采用的是内部指标：Calinski-Harabasz(CH)，Davies-Bouldin(DB)。
1. C H \mathrm{CH} CH 指标
C H \mathrm{CH} CH 指标通过类内离差矩阵描述紧密度, 类间离差矩阵描述分离度, 指标定义为
C H ( k ) = tr B ( k ) / ( k − 1 ) tr W ( k ) / ( n − k ) C H(k)=\frac{\operatorname{tr} B(k) /(k-1)}{\operatorname{tr} W(k) /(n-k)} CH(k)=trW(k)/(n−k)trB(k)/(k−1)
其中, n n n 表示聚类的数目, k k k 表示当前的类, tr B ( k ) \operatorname{tr} B(k) trB(k) 表示类间离差矩阵的迹, tr W ( k ) \operatorname{tr} W(k) trW(k) 表示类内
离差矩阵的迹。 C H C H CH 越大代表着类自身越紧密，类与类之间越分散, 即更优的聚类结果。
2. DB 指标
DB 指标通过描述样本的类内散度与各聚类中心的间距, 定义为
D B ( k ) = 1 K ∑ i = 1 K max j = 1 − k , j = i ( W i + W j C i j ) D B(k)=\frac{1}{K} \sum_{i=1}^{K} \max _{j=1-k, j=i}\left(\frac{W_{i}+W_{j}}{C_{i j}}\right) DB(k)=K1i=1∑Kj=1−k,j=imax(CijWi+Wj)
其中, K K K 是聚类数目, W i W_{i} Wi 表示类 C i C_{i} Ci 中的所有样本到其聚类中心的平均距离, W j W_{j} Wj 表示类 C i C_{i} Ci 中的
所有样本到类 C j C_{j} Cj 中心的平均距离, C i j C_{i j} Cij 表示类 C i C_{i} Ci 和 C j C_{j} Cj 中心之间的距离。可以看出, D B D B DB 越小表示类
与类之间的相似度越低, 从而对应越佳的聚类结果。
（3）ISODATA聚类分析+一元函数-参考“拍拍赚”APP（B154）
与k均值相比，ISODATA算法加入了一些试探步骤，并且可以结合成人机交互的结构，使其能利用中间结果所取得的经验更好地进行分类。【1】
（1）利用ISODATA进行聚类分析，得到聚类中心，以及各个任务点与聚类中心的距离。
（2）根据与聚类中心语句、定价绘制一元线性函数，与上述“FCM地理中心聚类（B353）”不同之处在于，本方法将所有聚类的信息汇总得到定价、距离，只绘制一个函数。而“FCM地理中心聚类（B353）”每个聚类中心绘制一个单独的函数。
2、自定公式法
（4）自定公式法（B315）
（1）根据供需关系，可得知会员密度和任务点密度都会影响定价，因此得到如下公式：
ρ 1 ( P , r ) = # { 会员Q: Q ∈ U r ( P ) } π r 2 , ρ 2 ( P , r ) = # { 任务点Q: Q ∈ U r ( P ) } π r 2 , \rho_{1}(P, r)=\frac{\#\left\{\text { 会员Q: } Q \in U_{r}(P)\right\}}{\pi r^{2}}, \rho_{2}(P, r)=\frac{\#\left\{\text { 任务点Q: } Q \in U_{r}(P)\right\}}{\pi r^{2}}, ρ1(P,r)=πr2#{ 会员Q: Q∈Ur(P)},ρ2(P,r)=πr2#{ 任务点Q: Q∈Ur(P)},
（2）根据经济学关系定性分析会员密度和任务点密度对任务定价的影响。
考虑某一个任务点,根据经济学原理, 会员密度 ρ \rho ρ 越高, 意味着有更多的会员可以去完成这项任务，价格显然应该下降; 而任务点密度 ρ 2 \rho_{2} ρ2 越高, 意味着该任务点附近还有很多任务可以去完成,价格也应该下降。因此， P i P_{i} Pi 与 ρ 1 , ρ 2 \rho_{1}, \rho_{2} ρ1,ρ2 均为负相关。
设 P i = G i ( ρ 1 , ρ 2 ) P_{i}=G_{i}\left(\rho_{1}, \rho_{2}\right) Pi=Gi(ρ1,ρ2).我们可以考虑两个比较简单的方案, 用如下公式表示:
公式 I: P = C ( 1 ρ 1 + 1 ρ 2 ) P=C\left(\frac{1}{\rho_{1}}+\frac{1}{\rho_{2}}\right) P=C(ρ11+ρ21), 其中 C C C 为常数.
公式 II: P = C ( 1 ρ 1 + ρ 2 ) P=C\left(\frac{1}{\rho_{1}+\rho_{2}}\right) P=C(ρ1+ρ21), 其中 C C C 为常数.
（3）计算两个公式的相关系数，得到第二个的相关系数更高（约0.64），故采用公式二作为定价方案。
（5）LOF离群因子（B477）
（1）猜想定价与用户配额、一定范围内的用户平均距离、任务的离群程度有关，根据散点图猜想函数关系。
1.用户配额
设定价为 p p p, 用户限额总和为 s s s, 根据散点分布情况，我们猜想的定价与限 额总额的函数关系为:
1 s + q 4 p = q 1 + q 2 ⋅ s + q 3 ⋅ s 2 s + q 4 \begin{aligned} &\frac{1}{s+q_{4}} p=\frac{q_{1}+q_{2} \cdot s+q_{3} \cdot s^{2}}{s+q_{4}} \end{aligned} s+q41p=s+q4q1+q2⋅s+q3⋅s2
其中 q 1 , q 2 , q 3 , q 4 q_{1}, q_{2}, q_{3}, q_{4} q1,q2,q3,q4 为系数。
2.用户平均距离
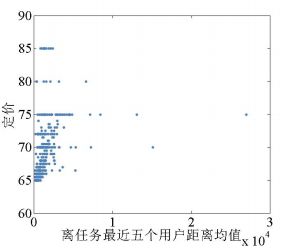
设定价为 p p p, 距离均值为 d ave d_{\text {ave }} dave , 根据散点分布情况，我们猜想的定价与密度 因素 2 的函数关系为:
p = q 1 ⋅ d ave + q 2 ⋅ d ave + q 3 p=q_{1} \cdot \sqrt{d_{\text {ave }}}+q_{2} \cdot d_{\text {ave }}+q_{3} p=q1⋅dave +q2⋅dave +q3
其中 q 1 , q 2 , q 3 q_{1}, q_{2}, q_{3} q1,q2,q3 为系数。
3.任务点离群程度
算法挺复杂，详情见原文，我比较好奇为什么不直接采用方差？
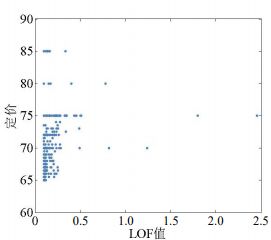
设定价为 p p p, LOF 值为 L L L, 根据散点分布情况，我们猜想定价与 LOF 离群 度的函数关系为:
p = q 1 ⋅ log ( L ) + q 2 ⋅ L + q 3 p=q_{1} \cdot \log (L)+q_{2} \cdot L+q_{3} p=q1⋅log(L)+q2⋅L+q3
其中 q 1 , q 2 , q 3 q_{1}, q_{2}, q_{3} q1,q2,q3 为系数。
（2）根据已有数据，分别代入上述公式，求系数和R^2等指标进行分析。
（6）自定公式法-参考出租车定价（B264）
为了保证任务能躳顺利完成和会员的基本收益, 对每项任务设定它的基础价格为 P 0 P_{0} P0, 结合上述的三个指标, 我们给出第 i i i 个任务的定价 P i P_{i} Pi :
P i = P 0 + 0.5 R i + S i − Q i P_{i}=P_{0}+0.5 R_{i}+S_{i}-Q_{i} Pi=P0+0.5Ri+Si−Qi
这里, P 0 P_{0} P0 为基础定价, 设为 65 , 其余指标转换值按如下方式给出：
3、任务未完成原因
（1）公式带入（B104）
（1）将未完成任务数据代入已求得的公式，得出定价偏低的判断。
（2）结论
1.任务末完成的主要原因是定价偏低, 使会员积极性下降。
2.存在地域特殊性, 如深圳地区末完成任务情况普遍。
3.可能存在不确定因素的影响，如天气不好、道路施工、交通堵塞、会员个人因
素等, 但不在本文的研究范围之内。
（2）未说明（B353）
未根据结果进行总结，但有提到“未完成任务集中于市中心并与中低价区高度重合,推测其未完成可能与会员行为选择有关。”。
（3）百度地图开放平台（B154）
（1）根据热度图分析不同定价完成与未完成的分布、以及价格和任务总数和完成率的关系。
（2）结论
1.我们可以发现末完成的任务主要集中在广州市以及深圳市, 而东莞市的任务则大名 都被很好地完成了。我们通过查阅三处城市的社会经济特征, 发现东莞市的经济发展状 况比广州市和深圳市的差, 并且人口以年轻人以及女性偏多。年轻人接受新鲜事物快, 并且一些在校学生以及全职太太更倾向于通过完成任务的方式获得一些报酬, 所以任务完成率更高。
2.通过上图我们发现定价高的任务完成的情况较好，在城市中心的任务完成情况也较好。在市中心是因为交通便利，会员容易到达，也因为市中心的人员更加密集，周围分布的会员多，任务更易被完成。
3.在价格为74元时完成率很低是由于价格在74元的任务总数较少，导致偶然性带来的波动较大，可以舍弃这一组数据。总的来看，我们发现在任务价格较低时,任务的完成率也会随之降低,而在任务价格较高时，任务完成情况较好。这是因为人们在有所选择的情况下更加倾向于去完成获得报酬高的任务来给自己带来更大的收益。
（4）根据任务分布（B315）
（1）绘制任务完成和未完成的分布图
（2）结论
1.依据经济发展水平定价的策略不合理。在经济发达区域整体价格偏低，任务对会员的吸引力不足，无法吸引足够多的人去完成，而这些地方又正是任务密集需要吸引大量会员参与的地方，因此导致了广州、深圳市中心等地区任务完成度的偏低。
2.当前定价模型考虑因素较少，通过卫星图可知交通便利程度并未被纳入定价考虑范围内，导致部分任务难度大、价格低，无人接受。
3.任务分配制度的不合理。信誉值较高者多分布于城区，他们的优先选择权使他们趋向于城郊定价更高的任务，而使城区内定价较低任务的完成率偏低。部分信誉较低的人被分配了较多任务却未完成，拉低了完成率。
4.不同地区存在的信息的不对称,导致实际完成情况出现了地区间的明显差异。
（5）根据自定公式对比完成与未完成任务（B477）
（1）任务点附件用户限额因素
部分未完成任务的拟合曲线低于已完成任务的拟合曲线，这说明这部分定价忽略了任务点附近用户限额因素而导致定价偏低，没有用户去选择执行这些任务。
（2）离任务点最近用户的平均距离因素
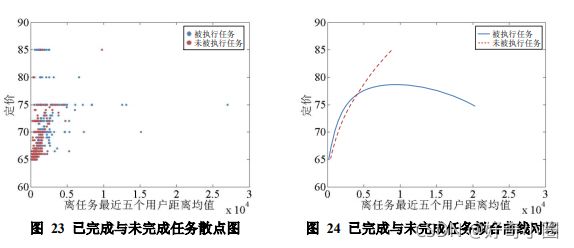大量的点都集中在交点之前，此时的拟合图像中，未完成任务的拟合曲线低于已完成任务的拟合曲线，这说明这部分定价忽略了任务点与离任务点最近用户的距离因素而导致定价偏低，没有用户去选择执行这些任务。对于交点以后的曲线走势，我们的解释是该段样本数据过少，有部分偶然离群点对拟合结果影响较大，导致未完成任务的曲线略高于已完成曲线。
（3）任务离散程度因素
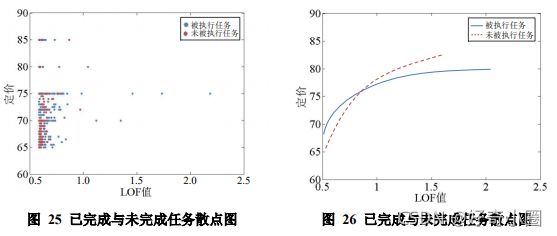
考虑到 90%以上的点的 LOF 值小于等于 1，大量的点都集中在交点之前，此时的拟合图像中，未完成任务的拟合曲线低于已完成任务的拟合曲线，这说明这部分定价忽略了任务离群程度因素而导致定价偏低，没有用户去选择执行这些任务。
（6）原因分析+举例+按原因绘制分布（B264）
例子略
（1）原因一：某些任务邻近区域内，任务密集，而会员人数远少于任务数，人均任
务量远远大于其实际完成能力。
（2）原因二：任务本身定价较低，使会员完成该任务的收益达不到期望值。某些
任务远离会员密集地，若会员要完成需花费较高的费用，且任务定价较低，使得回报低
于成本，故出现无人接单的情况。
（3）原因三：高收入地区会员对收益要求较高，导致很多任务没人接单。例如深圳
地区居民普遍收入较高，对收益也有较高的期望值，使得在其他地区能够完成的任务产
生的收益值不足以吸引他们去完成。
（4）原因四：高信誉会员的限额较高，预约过多任务，导致很多任务没及时完成。
某些任务周围有较多低信誉会员，但此任务被高信誉会员优先预约，而高信誉会员由于
多任务在身或此任务距离较远而没有完成。
（5）原因五：任务难度过高，导致任务性价比不高，或者任务所在地的周边环境，
如有交通故障难以通行、危险地带等原因，导致任务无法及时完成。
总结
想法
第一问要求算定价的原因和任务未完成的原因，第一反应就是找指标，然后分别进行多元线性回归和逻辑回归，就完事了。先绘制了散点图，观察到不会会员还是任务点，基本集中在珠三角，但结果不尽人意，后来又尝试了SVM、树甚至神经网络，但效果无一例外的很差，残差大，自举法正确率低，相关系数极小等等，散点图看的关系也并不明确。
反思
1.和队友都想到了该题很像美团外卖或者滴滴打车的模型，所以想要企图找到相关模型；但是忽略了直接找拍照赚钱的APP……
2.英语差，辗转了解到这是众包问题，于是查找相关论文，CSDN上有个文献推荐，挺好的，只是我看不懂众包综述——关于众包的一些研究方向
3.忘了筛选数据，如上所述，已经知道了数据基本主要集中在珠三角（画散点图时也发现了异常值，但直接给他“改正”了，实际这种做法并不合理）
4.缺少对数据特性的观察和对其背后原因的思索，其实在画散点图时就已经发现了未完成的任务主要集中在市区，具体是什么原因呢？没有想到……后来画了定价分布图，也忽略了和前边的联系
看国一论文时才发现，原因是“市区预期定价更高”。做数据题应该先“观察”，再“思考”，先把现象一条一条列出来，然后再思考背后的原因，探索其背后的联系。
5.忽略了普遍的经济规律，最开始拟定了很多指标，却忽略了“供需关系”这个最基本的原理，后来才开始考虑到任务和会员的供需关系。
6.过于执着完美模型，总想着让各项数据都很好看才行，但实际国一的拟合也并不是很好，因此对于给个结果让你猜原因的，同时涉及数据种类不多时，可以简单归因……当然更高的是结合现实中正在应用的模型（然而并不好找）
7.忽略了聚类。读到题目一时，不清楚是只看附件一的数据，还是要结合附件二里面的数据。实际国一的论文中两种方案都有，采用聚类和距离考量定价的论文，就是只看附件一的数据，着实巧妙。我还纠结了好久要如何把任务按照市分类，最初采用离哪个市中心近就归为那个市……显然不合理。果然在动手前要结合学过的方法多思考！不要盲目开始做题，以防陷入思维固化的陷阱，反复修改效率低下。
参考文献
（不标准的格式）
凡是引用到论文的，已在方法处标注出来对应文章。
【1】聚类算法——ISODATA算法 - 华东博客 - 博客园