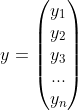机器学习算法——支持向量机SVM1(超平面)

支持向量机（Support Vector Machines, SVM）是一种基于统计学习理论的机器学习算法，是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器。

SVM学习的基本思想是求解能够正确划分训练数据集并且几何间隔最大的超平面。

那何为超平面？

很多讲解支持向量机的文章及视频一开始就讲超平面及其方程，对于没有基础的人来说很难理解。

首先先说明什么是超平面，超平面是一种数学上的概念，它是线上的一个点，也是平面上的一条直线，也是三维空间的一张平面。点、线、面都可以是超平面，但一般都不叫超平面，因为超平面是点、线、平面的推广，即大于三维的才叫超平面。

下面从点分割、线分割及面分割引出超平面表示方程。

· 点分割（一维划分）

下面是一个只有x轴的一维坐标轴，该轴同样存在圆点，x轴正方向和x轴反方向，且该轴上分布了很多点：

其中，红色的圆圈和绿色的菱形表示该坐标轴的样本点，那么如何在坐标轴上找一个分割点，来分割样本点，并要求此点的分割效果最好？寻找分割点很容易，但是如何去衡量该点就是最好的呢？

从坐标轴上看，要分的绿色的菱形和红色的圆圈在菱形坐标=-1和圆圈坐标=2就开始分了，那么在[-1,2]任取一点都可以将两个样本分开，要是找到最好的分割点，应该取两者中间的位置，即（-1+2）/2=0.5处。举个例子好理解，如果在村庄A和村庄B之间修公路，那么就需要选在两个村庄之间最靠近的那两户人间的中间修公路，这样既能保证两个村庄之间修一条公路而且不能干涉两村庄的生活。

·线分割（二维划分）

已知有5个红色的正例样本点x，坐标分别为D（0，1）、A（0，2）、E（1，1）、B（1，2）、C（2，2）；3个绿色的负例样本点o，坐标为G（2，1）、H（3，1）、F（3，2）

 现在要在两类样本点之间找一条直线将两类样本点分开，要求划分效果最好，如何做呢?

借鉴点分割的思想，将问题转化为求两点之间的距离，根据两点距离公式：

得出：

|AF|2=9、|BF|2=4、|CF|2=1、|DF|2=10、|EF|2=5、|AG|2=5、|BG|2=2、|CG|2=1、|DG|2=4、|EG|2=1、|AH|2=10、|BH|2=5、|CH|2=2、|DH|2=9、|EH|2=4

则两点之间最短的距离为1，相关的点为C（2,2）、E(1,1)、F(3,2)、G(2,1)。然后需要找到一条直线，使得样本点到此直线的距离相等且尽量最大。并且，由于要把两类样本分开，所以必然一部分样本点在直线上方，一部分在直线下方，根据直线的规律可知（斜率大于0），若（x0,y0）在直线上方，则满足AX0+By0+C>0，若（X0,y0）在直线下方，则满足Ax0+By0+C<0。具体步骤如下：

第一步，求点到直线的距离公式。

第二步，求这条直线的具体方程了。

假设该方程为Ax+By+C=0,则得到如下联立公式：

  E、C点代入大于0(因为E和C为正例)

 F、G点带入小于0（因为F和G为负例）

这样推导得出

A+B=0, A+2C=0

由于A、B均不为0，所以可以赋值A=1,则B=-1,C=-0.5，最终求得直线x-y-0.5=0,即下面这条蓝色直线。

·超平面分割（n维分割）

从一维到二维已经理解如何划分样本点了 ，但在实际问题中，导致一个时间发生的因素不会是单一因素或简单的两个因素（一个因素对应一个维度或一个特征），对于多个特征的情况，在数学上的表示就不再是二维直角坐标系可以表达的，有可能是三维坐标系、四维坐标系或者更高维度坐标系。此时划分样本的不再是一维里面的一个点，二维里面的一条直线，有可能是三维里面的一个平面，四维里面的一个超平面，此时可以把之前将的二维方程过渡到更高维度：

二维空间里，一条直线的方程为：Ax+By+C=0

三维空间里，平面的方程为：Ax+By+Cz+D=0，注意，平面的法向量为n=(A,B,C)

依次推广，n维空间的超平面方面表示为

x1,x2,x3,...,xn表示n维坐标系，各个维度的系统可以用w1,w2,w3,...,wn来表示，所以n维空间里面的超平面方程写成如下格式：

这里补充一个内积的概念：

设有n维向量

 

令,则称[x,y]为向量x与y的内积。

回归正题，将超平面方程可以变成[w,x]+b=0,即

所以，在样本空间中，任何一个超平面都可以用上述方程进行标识。其中,w=（w1,w2,...,wn）为法向量，b为位移项，也可以认为是截距，该超平面可以唯一的由此方程决定。并将该超平面记为（w,b）

参考：干货 | 从超平面到SVM（一）