【八大排序之插入和选择排序】

 写在前面

排序的重要性相信大家都早已经听老师提及，无论是笔试还是面试，几乎都会考查到排序问题。本次博主分享的是排序中的插入和选择排序，交换排序和并归排序将在下次博客分享，如果哪儿有什么不对的地方欢迎各位大佬在评论区中指正。

 

 

 

目录

 

 写在前面

1 插入排序

1.1 直接插入排序

1.2 希尔排序

 2 选择排序

2.1 直接选择排序

2.2 堆排序

---

 

1 插入排序

1.1 直接插入排序

基本思想：

• 直接插入排序是一种简单的插入排序法，其基本思想是：把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列 。 实际中我们玩扑克牌时，就用了插入排序的思想

• 当插入第i(i>=1)个元素时，前面的array[0],array[1],…,array[i-1]已经排好序，此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较，找到插入位置即将array[i]插入，原来位置 上的元素顺序后移
• 直接插入排序的特性总结：
• 1. 元素集合越接近有序，直接插入排序算法的时间效率越高
• 2. 时间复杂度：O(N^2)
• 3. 空间复杂度：O(1)，它是一种稳定的排序算法
• 4. 稳定性：稳定

注意事项：

为了分析方便我们后面排序都排的是升序，降序的代码会在注释中给予说明。假定我们在一个有序序列中插入一个数，我们用一个tmp保存当前数，然后拿前面的数与tmp比较，如果小于tmp,就把这个数往后挪动一个单位，再不断迭代下去，当不满足小于tmp时直接跳出循环，这样可以同时处理头插和中间插入的问题。但是这样做前提是前面数据必须有序，那么如果前面数据无序应该怎么办呢？

处理方法是套层循环，让其从第一个元素开始遍历，注意要控制结束条件,不要越界了。

具体代码:

void InsertSort(int* a, int sz)//最好情况是O(N)
{
	for (int i = 0; i < sz - 1; i++)
	{
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (a[end] > tmp)//降序就变成<
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}

		}
		a[end + 1] = tmp;
	}
}

通过代码发现直接插入排序的时间复杂度为O(N^2),但是如果数据是有序的那么就为O(N)。

1.2 希尔排序

基本思想：

• 希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数，把待排序文件中所有记录分成个组，所有距离为gap的记录分在同一组内，并对每一组内的记录进行排序。然后重复上述分组和排序的工作。当到达=1时，所有记录在统一组内排好序。

• 希尔排序的特性总结：
• 1. 希尔排序是对直接插入排序的优化。
• 2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。
• 3. 希尔排序的时间复杂度不好计算，需要进行推导，推导出来平均时间复杂度： O(N^1.3— N^2）
• 4. 稳定性：不稳定

 注意事项：

希尔排序的思想就是在直接插入排序的基础上进行的优化，先进行多次预排序让其大致有序，最后再进行一次直接插入排序，最后一次的直接插入排序是必不可少的。而预排的方法也是与直接插入排序类似，让相隔gap的数据相对有序，而gap的第一次大小我们一般取排序元素个数的二分之一或者三分之一，注意取三分之一的时候要加上1，否则gap最后就可能取不到1，导致排序不正确。

 具体代码：

void ShellSort(int* a, int sz)
{
	int gap = sz;
	while (gap)
	{
		gap /= 2;
		for (int i = 0; i < sz - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}

			}
			a[end + gap] = tmp;
		}
	}
}

通过代码我们发现希尔排序不是又多嵌套了一层循环，这样不是增加了其时间复杂度吗？

乍一看好像是这样一回事，但通过仔细分析我们可以发现通过预排序已经让数据大致有序了，而最后一次的直接插入排序将会进行的很快，顺序变动范围较小。

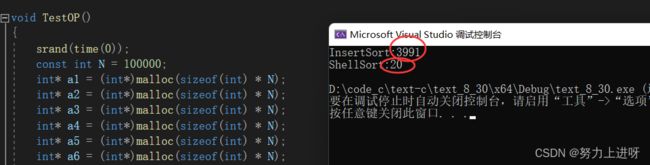
 我们可以测试一下直接插入排序与希尔排序的性能对比：

 由上图可知当排10W个数据时希尔排序的效率时直接插入排序的几百倍，数据越多，它们之间的差距只会越来越大。

---

 2 选择排序

2.1 直接选择排序

基本思想：

• 每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完 。

• 在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素，若它不是这组元素中的最后一个(第一个)元素，则将它与这组元素中的最后一个（第一个） 元素交换在剩余的array[i]--array[n-2]（array[i+1]--array[n-1]）集合中重复上述步骤，直到集合剩 余1个元素 。

• 直接选择排序的特性总结：
• 1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
• 2. 时间复杂度：O(N^2)
• 3. 空间复杂度：O(1)
• 4. 稳定性：不稳定

 直接选择排序的思想很简单，代码写起来也比较容易，这里就直接上具体代码：

void SelectSort1(int* a, int sz)
{
	int i = 0;
	int j = 0;
	for (i = 0; i < sz; i++)
	{
		int k = i;
		for (j = i + 1; j < sz; j++)
		{
			if (a[k] > a[j])
			{
				k = j;
			}
		}
		Swap(&a[i], &a[k]);
	}
}

这里还可以用双下标的方法优化一下直接选择排序，让其效率比第一种要高一些，但是时间复杂度还是O(N^2),具体代码：

void SelectSort2(int* a, int sz)
{
	int begin = 0;
	int end = sz - 1;
	while (begin < end)
	{
		int mini = begin;
		int maxi = begin;
		for (int i = begin; i <= end; i++)
		{
			if (a[i] < a[mini])
			{
				mini = i;
			}
			if (a[i] > a[maxi])
			{
				maxi = i;
			}
		}
		Swap(&a[begin], &a[mini]);
		if (a[begin] == a[maxi])
		{
			maxi = mini;
		}
		Swap(&a[end], &a[maxi]);
		begin++;
		end--;
	}
}

这种方法里面值得注意的是如果第一个元素就是最大值,当与最小值交换后，该位置就已经不是最大值了，所以要特殊处理。

2.2 堆排序

在之前我们就已经知道什么是堆（大堆和小堆），而堆中也有一些我们必须要记住的公式

parent=(child-1)/2 ;   child可以是左孩子，也可以是右孩子

leftchild=parent*2+1;

rightchild=parent*2+2;

实现堆排序我们还得必须掌握向下调整堆的算法。

向下调整堆的算法要使用必须满足左子树和右子树必须是大堆（小堆）

具体代码（以建大堆为例）：

void AdjustDown(int* a, int sz, int root)
{
	int parent = root;
	int child = parent * 2 + 1;
	while (child < sz)
	{
		if (a[child + 1] > a[child] && child + 1 < sz)
		{
			child++;
		}

		if (a[parent] < a[child])
		{
			Swap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

 这里面我们假设左孩子小于右孩子，当不满足条件时就让child++,还得判断

 

 但如果左右子树并不是大堆（小堆）那应该怎么办呢？

我们的处理方法是从倒数第二排的非叶子结点（也就是最后一个元素的父亲）开始建堆，直到第一个元素为止，具体代码如下：

for (int i = (sz - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, sz, i);
	}

这样就完成了建堆，那么建堆的时间复杂度是多少呢？

这里我们可以来计算一下：

我们假设该二叉树为满二叉树（由于时间复杂度计算的只是大概值，所以假设成满二叉树时OK的），树高为h.

由于第一层（1个元素）最多调整h-1次，

第二层（2个元素）最多调整h-2次，

第三层（4个元素）最多调整h-3次，

…………

第（h-1）层（2^(h-2)个元素） 最多调整1次

只需要调整到（h-1）层就行了。

所以得出：t(n)=2^0*(h-1)+2^1*(h-2)+2^2*(h-3)+……2^(h-2)*1

然后用错位相减法就可以得出：t(n)=2^h-h-1; 由于是完全二叉树h=log(i+N) (以2为底），

带入得t(n)=N-log(N+1)   当N区域无穷大得时候 t(n)=N; 故其建堆的时间复杂度为O(N).

堆建好了后我们还要思考一个问题  排升序建大堆还是建小堆？

 如果我们建小堆，那么最小数在堆顶已经被选出来了，那么就要在剩下的数中去选数，但是剩下结构都乱了，需要重新建堆选数，建堆的时间复杂度为O(N),那么总的时间复杂度为O(N^2),这样堆排序就没有了效率，所以排升序建小堆不可取，我们要建大堆。

 那么大堆建立好了后我们应该怎样选数呢？

首先先建好大堆，将第一个元素（最大的元素）与最后一个元素交换，此时除了第一个元素外，剩下堆的结构并没有被破坏，再将第一个元素拿来建堆，再让元素个数--（最大数已经选出），然后不断迭代下去直至第一个元素，此时总的时间复杂度为N*log(N) (由于只是需要调整高度次，所以为logn)。

具体代码：

void HeapSort(int* a, int sz)
{
	for (int i = (sz - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, sz, i);
	}

	int end = sz - 1;
	while (end)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}

}

堆排序的特性总结：

1. 堆排序使用堆来选数，效率就高了很多。

2. 时间复杂度： O(N*logN)

3. 空间复杂度： O(1)

4. 稳定性： 不稳定

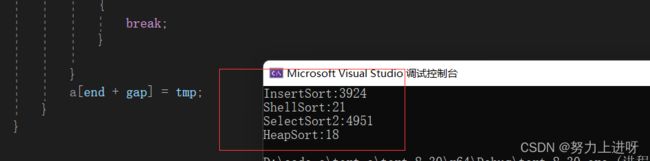
 我们来看看这四种排序的效率对比：

 由图可以直观看出堆排序和希尔排序的效率比较高，直接插入和直接选择的效率较低。

---

 好了，今天的分享就到这里了，如果对你有帮助的话能不能支持一下博主呢？