离散信号的相加和相乘(matlab实现)
离散信号的相加和相乘
原始信号
clear all;
clc;
n1=[-5:4]; %序列x1(n)的时间起始和终止位置
n1s=-5;n1f=4;
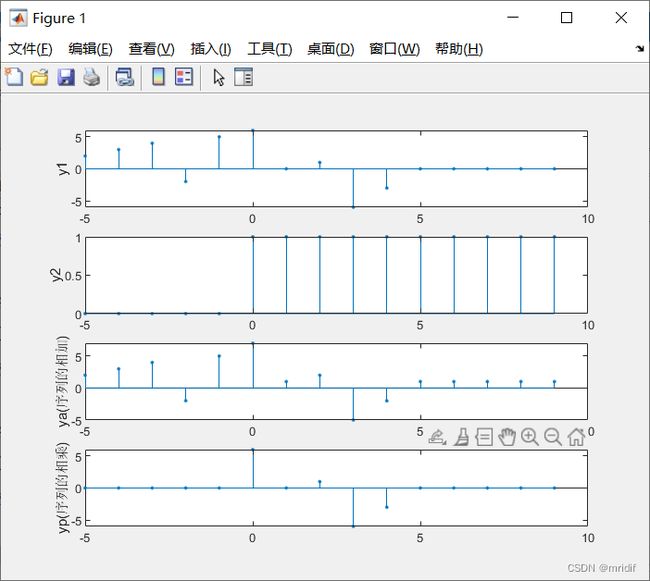
x1=[2,3,4,-2,5,6,0,1,-6,-3]; %序列x1(n)不同时间的幅值
n2=[0:9]; %序列x1(n)的时间起始和终止位置
n2s=0;n2f=9;
x2=[1,1,1,1,1,1,1,1,1,1]; %序列x2(n)不同时间的幅值
信号定义部分
ns=min(n1s,n2s);nf=max(n1f,n2f); %新序列的时间起始和终止位置
n=ns:nf; %新序列范围是[-5,9]
y1=zeros(1,length(n)); %延拓序列初始化
y2=zeros(1,length(n));
y1(find((n>=n1s)&(n<=n1f)==1))=x1; %将延拓序列y1幅值x1(寻找n1s到n1f的值,成立即赋值x1序列的值,不成立则为0)
y2(find((n>=n2s)&(n<=n2f)==1))=x2; %将延拓序列y2幅值x2
y3=y1+y2; %逐点相加
y4=y1.*y2; %逐点相乘,.*的意思是每个元素都相乘
序列相加 : 两个不同的序列相加 , 相同的 n 位置的点相加 ;
序列相乘:对应采样点之间的相乘;
信号的绘图部分
figure;
subplot(4,1,1),stem(n,y1,'.'); %绘制序列y1
line([n(1),n(end)],[0,0]) %画x轴,n(1)是n的第一个数,即-5;n(end)是n的最后一个数,即9;
%[0,0]即绘制y轴连线,可以将n(end)改成n(end-1),[0,0]改成[-10,10]便可以明显看出代码含义
ylabel('y1');
subplot(4,1,2),stem(n,y2,'.'); %绘制序列y2
line([n(1),n(end)],[0,0]) %画x轴
ylabel('y2');
subplot(4,1,3),stem(n,y3,'.'); %绘制序列y3
line([n(1),n(end)],[0,0]) %画x轴
ylabel('ya(序列的相加)');
subplot(4,1,4),stem(n,y4,'.'); %绘制序列y4
line([n(1),n(end)],[0,0]) %画x轴
ylabel('yp(序列的相乘)');
序列长度问题
已知序列x1(n)和序列x2(n)都是从0开始的有限长序列,x1(n)的长度为5,x2(n)长度为7,则x1(n+2)+x2(n)和x1(n)*x2(n)的长度点数(有效长度)分别为9,5