图神经网络/GNN(三)-基于图神经网络的节点表征学习

Task3概览：

在图任务当中，首要任务就是要生成节点特征，同时高质量的节点表征也是用于下游机器学习任务的前提所在。本次任务通过GNN来生成节点表征，并通过基于监督学习对GNN的训练，使得GNN学会产生高质量的节点表征。主要内容为：

• 经典图神经网络（GCN、GAT）的原理

• 基准数据集介绍与使用

• 基于图卷积层的节点预测任务实战

• 对比实验结果分析

一、经典图神经网络（GCN、GAT）的原理

图神经网络有很多种不同的变体，单就图卷积操作这一点来说研究者门就提出了非常多的方法，PyG包为这些方法的使用提供了便捷的渠道，详见下述链接：

https://pytorch-geometric.readthedocs.io/en/latest/modules/nn.html#convolutional-layers

GCN和GAT是两种比较通用和熟悉的图网络模型，其实两者在一些思想上是比较相似的，如果结合起来一起看可能会更加容易理解一些。

1.1 GCN原理

GCN全称Graph convolutional network，图卷积网络。GCN于2017年提出，它的到来标志着图神经网络时代的出现。

GCN与我们常见的CNN（卷积神经网络）听起来名字很相似，其实理解起来也比较类似，都可以理解为是一种特征提取器。不同的是，CNN提取的是张量数据特征，而GCN提取的是图结构数据特征。

GCN网络层的基础公式如下：

$H^{l+1}=\sigma ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^l{w}^l)$

其中，

• $H^l$指的是第l层的输入特征，$H^{l+1}$是这一层的输出特征。$w^l$ 指线性变换矩阵，是用来学习的参数。 $\sigma (.)$是非线性激活函数，如ReLU、Sigmoid等。

• 另外重点是A和D。I是单位矩阵，A是图结构的邻接矩阵。由于节点与自身并无边相邻，所以邻接矩阵中的对角线自然都是0。但是在进行下游集散时，如此无法在邻接矩阵体现“自身节点”的信息，所以将A加上一个单位矩阵Id得到带自环边的A矩阵，也就是$\tilde{A}$。

• $\tilde{D}$是自连邻接矩阵的度矩阵。${\tilde{D}}^{-\frac{1}{2}}$就是在自连度矩阵D的基础上开平方根取逆。由于${\tilde{D}}^{-\frac{1}{2}}$是一个对角阵，所以直接可以通过给每个元素开根取倒数的方式得到 ${\tilde{D}}^{-\frac{1}{2}}$。

所以说，GCN公式中的${\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$这些其实都是从邻接矩阵计算过来的，甚至可以将其看做一个常量，我们的图神经网络模型需要学习的仅仅是$w^l$这个权重矩阵。

为了便于理解，可以从矩阵图解的方式来理解GCN公式。首先下图是$\tilde{A}{H}^l$这一计算的意义：

如果对矩阵见点乘的运算规则比较了解的话，可以将上图理解为一个线性变化的计算过程。在自连邻接矩阵满足上图的数据场景时，下一层第一个节点的向量表示就是当前层节点h1,h2,h3,h5这些节点向量表示的和，这一过程的可视化意义如下图所示：

以上过程其实是一个消息传递的过程，sum pooling就是一种消息聚合的操作，当然也可以采用Average、Max等池化操作。经过这样的消息传递操作后，下一层的节点1就聚集了它的一阶邻居与自身的信息，这就很有效地保留了原始图结构数据内部所蕴含的信息。

最后特别关注一下度矩阵D在整个过程中起到的作用。节点的度代表着某一节点一阶邻居的数量，所以乘以矩阵的逆也就稀释掉度很大节点的重要度。

这个地方可以用一个例子理解，例如下图，保险经理B的好友有1000个，当然你也是其中的一个；而你小时候的青梅竹马A加上你仅有10个好友，那么A、B对于定义你的权重自然也就不一样了。

${\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^l$这一计算的可视化意义如下：

图神经网络之所以有效，就是因为它很好地利用了图结构的信息。

1.2 GAT原理

GAT全称Graph Attention Netwoik，图注意力网络。GAT是指加入了注意力机制的图神经网络，其消息传递的权重是通过注意力机制得到。

GAT的计算过程如下：

$a_{ij}={\mathrm{softmax}}_j(e_{ij})=\frac{\exp (e_{ij})}{{\sum }_{k\in N_i}\exp (e_{ik})}$

$e_{ij}=\text{ LeakyReLU }({\alpha }^T[W{h}_i\Vert W{h}_j])$

• $h_i$和$h_i$是当前输入层的节点i与节点j的特征表示，$W$是线性变换矩阵，形状是$W\in R^{F\times F^{\prime }}$，其中$F$就是输入特征的维度， $F^{\prime }$是输出特征的维度；

• $||$是向量拼接操作，原本维度为$F$的$h_i$与$h_j$经过$W$线性变换后维度均变为$F^{\prime }$ ，经过拼接后得到维度为$2F^{\prime }$的向量。此时再点乘一个维度为$2F^{\prime }$的单层矩阵$\alpha$的转置，然后经LeakyReLU激活后得到1维的$e_{ij}$。

• 得到所有的$e_{ij}$后，再进行softmax操作，得到注意力权重$a_{ij}$。

计算节点i的在当前GAT网络层的输出向量即可描述为：

$h_i^{\prime }=\sigma ({\sum }_{j\in N_i}{\alpha }_{ij}W{h}_j)$

其中，$\sigma (.)$代表任意激活函数，$N_i$代表节点$i$的一阶邻居集，$W$与注意力计算中的$W$是一样的。

1.3 GCN与GAT的异同

GCN和GAT它们同时考虑了节点自身信息与周围节点的信息，因此在节点表征学习中应该由于只考虑节点自身属性，而忽略了节点之间的连接关系的MLP。也就是说，对周围邻接节点信息的考虑，是图神经网络优于普通深度神经网络的原因。

如果将GCN与GAT放在一起看，两者其都是采用了加权聚合的消息传递方式进行图特征的提取过程，如下图所示。最后聚合得到的信息不近包括邻居节点的特征信息，还包含了图的一些结构信息。

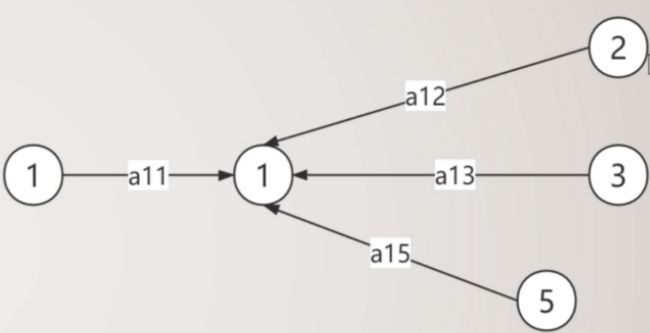
而GCN与GAT两者主要的区别在于权重的选取上，GCN使用的是一个基于度的加权求和，而在GAT中是基于注意力的加权求和。

二、基准数据集介绍及使用

2.1 常见基准数据集

Pythorch Geometric（简称PyG）包含有大量常见的数据集，例如Planetoid数据集、QM7和QM9数据集以及一些3D网格/点云数据集，如FAUST、ModelNet10/40和ShapeNet等。PyG中涉及的数据集链接如下。

https://pytorch-geometric.readthedocs.io/en/latest/modules/datasets.html

其中Planetoid数据集使用比较常见，主要由Cora、Citeseer、Pubmed三个子数据集组成，并称“御三家”。各数据集的实际含义如下所示：

• Cora：一个根据科学论文之间相互引用关系而构建的Graph数据集合，论文分为7类：Genetic_Algorithms，Neural_Networks，Probabilistic_Methods，Reinforcement_Learning，Rule_Learning，Theory，共2708篇；

• Citeseer：一个论文之间引用信息数据集，论文分为6类：Agents、AI、DB、IR、ML和HCI，共包含3312篇论文；

• Pubmed：生物医学方面的论文搜寻以及摘要数据集。

2.2 基准数据集的使用

初始化是使用数据集的第一步。

数据集的初始化将自动下载其原始文件并将其处理为方便后续处理的数据格式。

下面以常见的Cora数据集为例进行介绍：

如下所示，Cora数据集中只有一个图，该图包含2708个节点，10556条边，节点类别数为7，特征维数为1433。这里已经对Cora数据集进行了划分，分为了训练集、验证集和测试集。

import torch
from torch_geometric.datasets import Planetoid

dataset = Planetoid(root='/dataset/Cora', name='Cora')    # 导入数据集

len(dataset)   # 查看数据集的长度
# 1

dataset.num_classes   # 查看数据集的类别数 
# 7
 
dataset.num_node_features   # 查看数据集的节点特征数数
# 1433

data = dataset[0]
data.num_nodes   # 查看数据的节点个数
# 2708

data.num_edges   # 查看数据的边个数
# 10556

除了可以用代码查看一些常见的属性外，还可以对数据集进行简单的分析。

• 输出train_mask和test_mask的结果进行观察；

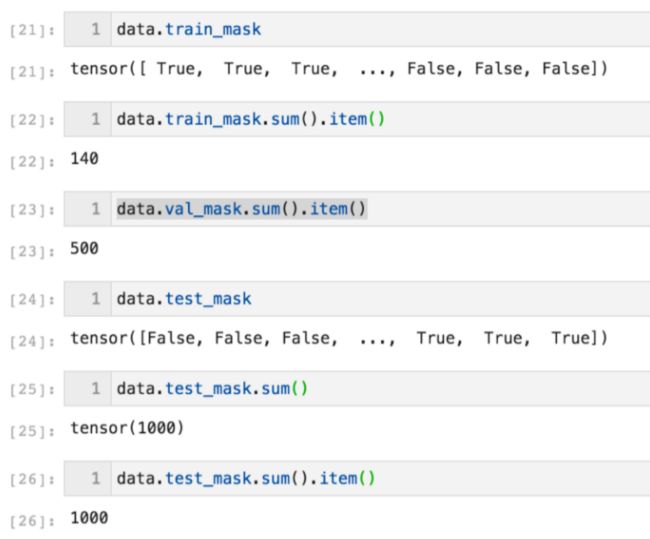
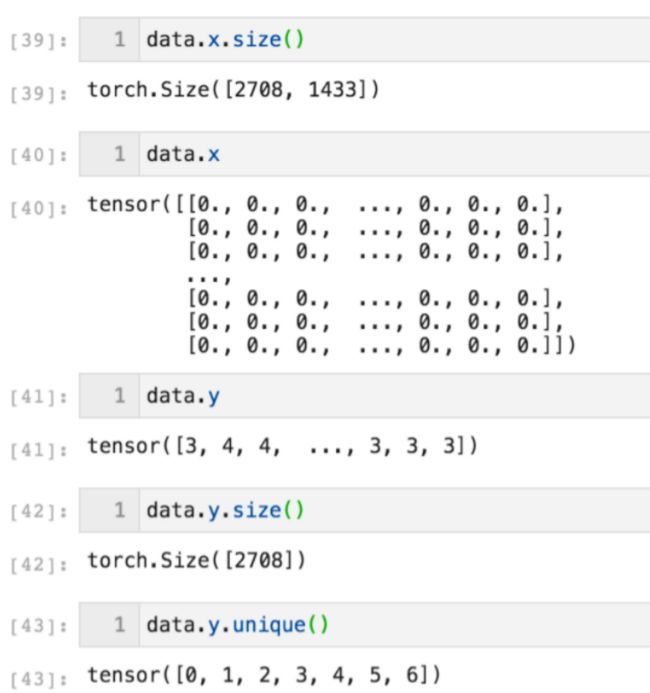
• 然后看看节点特征和标签。x为节点特征矩阵，维度为2708*1433。y为节点标签向量，维度为2708，类别为7。

三、基于图卷积层的节点分类任务实战

接下来就可以构建一个简单的GCN模型，在Cora数据集上进行半监督节点分类。

3.1 获取数据集

from torch_geometric.datasets import Planetoid
from torch_geometric.transforms import NormalizeFeatures

dataset = Planetoid(root = 'Dataset', name = 'Cora', transform = NormalizeFeatures())

print(f'Dataset: {dataset}:')
print('======================')
print(f'Number of graphs: {len(dataset)}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')

data = dataset[0]  # Get the first graph object.

# Gather some statistics about the graph.
print(f'Number of nodes: {data.num_nodes}')
print(f'Number of edges: {data.num_edges}')
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}')
print(f'Number of training nodes: {data.train_mask.sum()}')
print(f'Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}')
print(f'Contains isolated nodes: {data.contains_isolated_nodes()}')
print(f'Contains self-loops: {data.contains_self_loops()}')
print(f'Is undirected: {data.is_undirected()}')

数据转换在将数据输入到神经网络之前修改数据，这一功能可用于实现数据规范化或数据增强 。在此例子中，我们使用NormalizeFeatures，进行节点特征归一化，使各节点特征总和为1。其他数据转换方法请参阅torch-geometric-transforms。

3.2 可视化节点表征分布

import matplotlib.pyplot as plt
from sklearn.manifold import TSNE

def visualize(h, color):
    z = TSNE(n_components=2).fit_transform(out.detach().cpu().numpy())
    plt.figure(figsize=(10,10))
    plt.xticks([])
    plt.yticks([])

    plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="Set2")
    plt.show()
    
 # 可视化调用
 model.eval()

 out = model(data.x, data.edge_index)
 visualize(out, color=data.y) 

为了实现节点表征分布的可视化，我们先利用TSNE将高维节点表征嵌入到二维平面空间，然后在二维平面空间画出节点。

3.3 图神经网络的构造

理论上，应该能够仅根据文件的内容，即它的词包特征表示（bag-of-words feature representation）来推断文章的类别，而无需考虑文章之间的任何关系信息。

接下来本文将分别构建简单的MLP和GCN网络，来对实际的分类效果进行实验。其中，MLP网络只对输入节点的特征进行操作，它在所有节点之间共享权重；而GCN网络还可以利用网络节点间的连接信息。

通过torch.nn.Linear layers可以很方便地构建MLP layers和GCN Conv layers，从而轻松构建MLP模型和GCN模型。

import torch
from torch.nn import Linear
import torch.nn.functional as F

class MLP(torch.nn.Module):
    def __init__(self, hidden_channels):
        super(MLP, self).__init__()
        torch.manual_seed(12345)
        self.lin1 = Linear(dataset.num_features, hidden_channels)
        self.lin2 = Linear(hidden_channels, dataset.num_classes)

    def forward(self, x):
        x = self.lin1(x)
        x = x.relu()
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.lin2(x)
        return x

model = MLP(hidden_channels=16)
print(model)

MLP由两个线程层、一个ReLU非线性层和一个dropout操作。第一线性层将1433维的特征向量嵌入（embedding）到低维空间中（hidden_channels=16），第二个线性层将节点表征嵌入到类别空间中（num_classes=7）。

from torch_geometric.nn import GCNConv

class GCN(torch.nn.Module):
    def __init__(self, hidden_channels):
        super(GCN, self).__init__()
        torch.manual_seed(12345)
        self.conv1 = GCNConv(dataset.num_features, hidden_channels)
        self.conv2 = GCNConv(hidden_channels, dataset.num_classes)

    def forward(self, x, edge_index):
        x = self.conv1(x, edge_index)
        x = x.relu()
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.conv2(x, edge_index)
        return x

model = GCN(hidden_channels=16)
print(model)

将torch.nn.Linear layers 替换为PyG的GNN Conv Layers。

GCN模型包含两个图卷积层。第一层输入维度为1433（节点特征维度），输出为16（与第一层输出一致），后面接上一个relu激活函数，以及dropout操作。第二层输入维度为16，输出为7（节点标签数量），后接log_softmax函数进行分类。

3.4 图神经网络的训练

利用交叉熵损失 和Adam优化器 来训练神经网络。

model = GCN(hidden_channels=16)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()

def train():
    model.train()
    optimizer.zero_grad()  # Clear gradients.
    out = model(data.x, data.edge_index)  # Perform a single forward pass.
    loss = criterion(out[data.train_mask], data.y[data.train_mask])  # Compute the loss solely based on the training nodes.
    loss.backward()  # Derive gradients.
    optimizer.step()  # Update parameters based on gradients.
    return loss

for epoch in range(1, 201):
    loss = train()
    print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')

上面的GCN模型包含两个图卷积层。第一层输入维度为1433（节点特征维度），输出为16（与第一层输出一致），后面接上一个relu激活函数，以及dropout操作。第二层输入维度为16，输出为7（节点标签数量），后接log_softmax函数进行分类。

3.5 图神经网络的测试

最后在测试集上评估模型，计算分类正确率并显示。

def test():
    model.eval()
    out = model(data.x, data.edge_index)
    pred = out.argmax(dim=1)  # Use the class with highest probability.
    test_correct = pred[data.test_mask] == data.y[data.test_mask]  # Check against ground-truth labels.
    test_acc = int(test_correct.sum()) / int(data.test_mask.sum())  # Derive ratio of correct predictions.
    return test_acc

test_acc = test()
print(f'Test Accuracy: {test_acc:.4f}')

四、对比实验结果分析

经过前面三个部分的介绍，我们了解了经典图神经网络GCN和GAT的基本原理、常见的基准数据集以及基于图卷积层的节点分类代码实现。由于图神经网络的不同构造和细节会对任务的精度产生影响，同时在不同数据集上也可能会有不一样的表现，因此本节通过两个小实验来初步探究分析不同图卷积层在不同图基准数据集上的表现。

4.1 不同图卷积模块实验

不同图卷积模块（14种）和MLP的实验结果如下图所示。

• 从测试集精度的角度看，MLP仅有59%的精度（红色柱），而其他图卷积模块的测试精度普遍在70%以上，由此可知，学习了图结构信息的网络结构明显具有更好的效果。一共有5种图卷积模型的测试集精度超过了80%（天蓝色柱），其中FeaStConv取得了最佳效果，精度达到82.1%（深蓝色柱）。

• 从模型训练时间（PyTorch CPU版本，训练200代）的角度看，约73%（11/15）的模型训练时间在50秒以内，其中有5种模型的训练时间维持在10秒内，速度非常之快。但是少数几个模型的训练时间异常长，最长的达到7分钟，具体原因等待学习相关模型原理后进一步解释分析。

• 由以上分析结果可知，采用了图卷积模块有利于图任务的学习，不同的图卷积模块将会对节点表征的学习效果产生不一样的影响。根据实验结果综合评估，FeaStConv具有最为优异的性能，原因在于其具有最高的精度，同时模型训练时间也处于一个可以易于接受的水平；此外，GCNConv、HypergraphConv等图卷积模块也是不错的选择，可依据实际情况选择性使用。

4.2 不同数据集实验

根据前面的实验结果，选取8个性能优异的图卷积模块在3种典型的分类图数据集（Cora、CiteSeer、PubMed）上进行实验，观察实验结果。

选择的图卷积模块有FeaStConv、GCNConv、HypergraphConv 、GATConv、SAGEConv、TransformerConv 、ARMAConv、SuperGATConv。

• 实验结果可以看出，不同的图卷积模型在Cora、CiteSeer数据集上呈现出较大的精度差异，而在PubMed数据集上的精度相差不大，几乎都位于77%-78%之间。

• 同时，并没有哪一种图卷积模型在所有数据集上均取得最佳效果，这说明了没有放之四海而皆准的通用模型，需要根据实际应用问题来选择合适的图卷积模型。

• 为进一步提升图任务的性能，除了在图卷积层进行改进外，还可以对池化、归一化等方面做出进一步调整，以求实现最佳的模型性能。

除了图卷积模块外，可能还有其他模块会影响到图任务的性能，因此后续思考学习如何改进其他模块，以进一步提升图任务的性能。

Task3学习心得：

第一次用代码跑出图学习任务的结果还是比较兴奋，其中必须离不开Datawhale团队组织和整理的组队学习项目和细致的学习资料，感谢！

当然，要明白这只是一个很简单的入门任务而已，图神经网络的数学原理、代码的改进、与实际应用的融合，这些都需要继续学习，任重而道远。好好学习，天天向上~

---

参考资料

1. Datawhale组队学习【图神经网络】
2. PyTorch图神经网络实践（三）使用基准图数据Cora进行半监督节点分类_Javy Wang-CSDN博客_cora数据集
3. 图神经网络（5)_GCN原理与代码
4. 图神经网络（6)_GAT原理与代码