深度学习06——逻辑斯蒂回归

目录

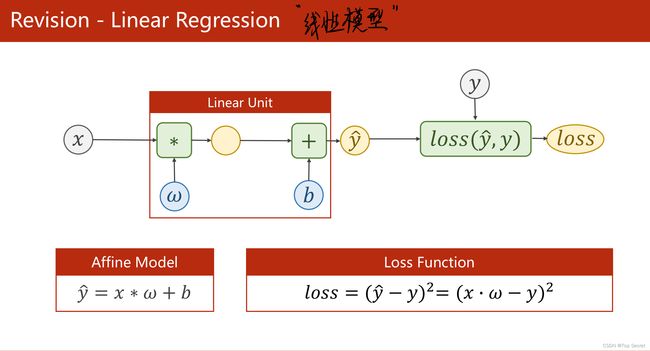
1. 线性模型回顾

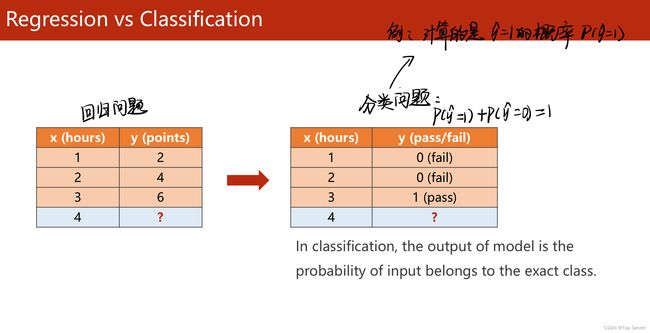
2.做分类问题：逻辑斯蒂回归模型

2.1 常见数据集

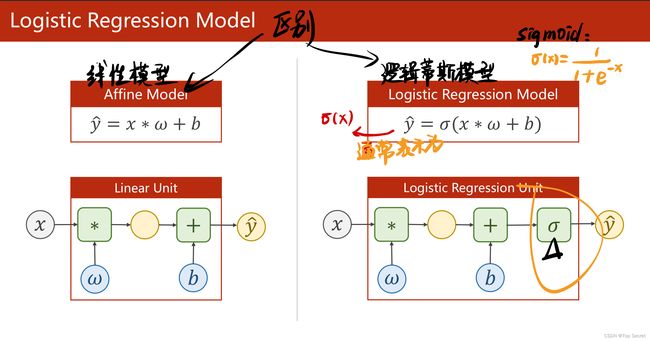
2.2 逻辑回归与线性回归的区别

 2.3 逻辑回归使用的损失函数和优化器

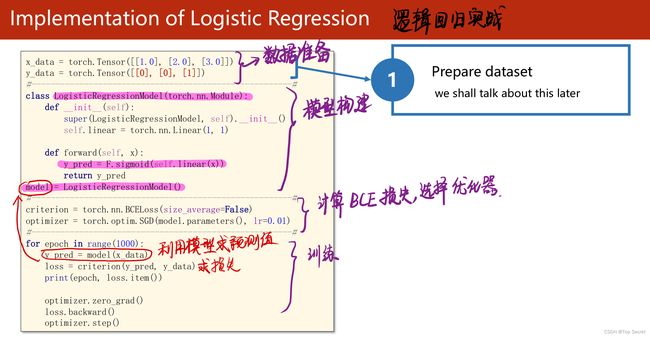
 2.4 模型构建

2.4.1 torch.sigmoid()、torch.nn.Sigmoid()和torch.nn.functional.sigmoid()三者之间的区别

2.4.2 二分类的交叉熵（BCELoss）

2.4.3 代码一览 

2.5  pytorch代码

2.5.1 对比代码学习

2.5.2 BCE loss的理解代码

---

结合下文辅助学习：
传送门 

1. 线性模型回顾

 

2.做分类问题：逻辑斯蒂回归模型

2.1 常见数据集

torchvision 模块

2.2 逻辑回归与线性回归的区别

 

 2.3 逻辑回归使用的损失函数和优化器

 

 2.4 模型构建

2.4.1 torch.sigmoid()、torch.nn.Sigmoid()和torch.nn.functional.sigmoid()三者之间的区别

torch.sigmoid():
这是一个方法，包含了参数和返回值。

torch.nn.Sigmoid():
可以看到，这个是一个类。在定义模型的初始化方法中使用，需要在_init__中定义，然后在使用。

 

torch.nn.functional.sigmoid():
这其实是一个方法，可以直接在正向传播中使用，而不需要初始化。**在训练模型的过程中，也可以使用。**例如：

 

 

这三个sigmoid()实现的功能是一样的，没有区别。
 

2.4.2 二分类的交叉熵（BCELoss）

2.4.3 代码一览 

 

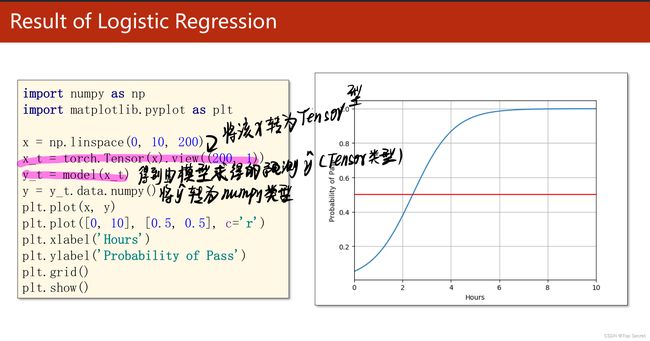
2.5  pytorch代码

import torch
import torch.nn.functional as F  #该模块中含有较多激活函数

x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[0],[0],[1]])

class LogisticRegresssionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegresssionModel,self).__init__()
        self.linear = torch.nn.Linear(1,1)

    def forward(self,x):
        y_pred = F.sigmoid(self.linear(x)) #非线性化线性数据
        return y_pred

model = LogisticRegresssionModel()

#选择损失函数与优化器
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(),lr=0.01)

for epoch in range(100):
    y_pred = model(x_data)  #做预测
    loss = criterion(y_pred,y_data) #求损失
    print("当前的epoch:",epoch,'loss的值为：',loss.item()) #拿到loss的值需要.item()

    optimizer.zero_grad() #梯度清零
    loss.backward() 
    optimizer.step() #更新参数

结果：
 

2.5.1 对比代码学习

import torch

# import torch.nn.functional as F

# prepare dataset
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])


# design model using class
class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)

    def forward(self, x):
        # y_pred = F.sigmoid(self.linear(x))
        y_pred = torch.sigmoid(self.linear(x))
        return y_pred


model = LogisticRegressionModel()

# construct loss and optimizer
# 默认情况下，loss会基于element平均，如果size_average=False的话，loss会被累加。
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# training cycle forward, backward, update
for epoch in range(1000):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())

x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)

2.5.2 BCE loss的理解代码

import math
import torch
pred = torch.tensor([[-0.2],[0.2],[0.8]])
target = torch.tensor([[0.0],[0.0],[1.0]])
 
sigmoid = torch.nn.Sigmoid()
pred_s = sigmoid(pred)
print(pred_s)
"""
pred_s 输出tensor([[0.4502],[0.5498],[0.6900]])
0*math.log(0.4502)+1*math.log(1-0.4502)
0*math.log(0.5498)+1*math.log(1-0.5498)
1*math.log(0.6900) + 0*log(1-0.6900)
"""
result = 0
i=0
for label in target:
    if label.item() == 0:
        result +=  math.log(1-pred_s[i].item())
    else:
        result += math.log(pred_s[i].item())
    i+=1
result /= 3
print("bce：", -result)
loss = torch.nn.BCELoss()
print('BCELoss:',loss(pred_s,target).item())

注：文章为自我学习记录，欢迎讨论，侵删