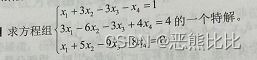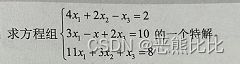Matlab_Study
1.基本操作
1.1 计算
1.2 数值显示格式
format style #设置指定格式
format #默认为short
| 格式 | 说明 |
|---|---|
| short | 默认,保留四位小数 |
| long | 保留十五位小数 |
| hex | 十六进制 |
| + | 正负和0分别用+、-、tab表示 |
| … |
1.3 常用快捷指令
| 作用 | 命令 |
|---|---|
| 清屏 | clc |
| 清理内存 | clear |
| 历史记录 | 箭头“↑” |
| 显示或改变当前目录 | cd |
| 显示当前目录或指定目录下的文件 | dir |
| 调用dos命令 | ! |
| 退出matlab | exit |
| 保存 | save |
1.4 标点符号说明
| 标点 | 说明 |
|---|---|
| , | 分割符 |
| . | 小数点或结构数组的域访问符 |
| ; | 矩阵行与行分割符、不显示计算结果 |
| : | 生成一维数组、表示一维数组的全部元素或多维中的某一维全部 |
| % | 注释符 |
| ‘’ | 字符串标识符 |
| … | 分行链接 |
| = | 赋值 |
| [] | 向量、矩阵标识符、函数输出符 |
| {} | 构造单元数组 |
| _ | 名称链接 |
| @ | 函数句柄、形成用户对象类目录 |
1.5 MATLAB示例
示例1:命令行窗口表达式
>> A = 2*pi/2+2^3/8-0.3e-3 #输入表达式
A =
4.141292653589793
>> who #内存变量
您的变量为:
A ans
示例2:多条曲线示例
>> t=0:pi/6:2*pi;
>> y0=exp(t/5);
>> y=exp(t/5).*sin(2*t);
>> plot(t,y,t,y0,t,-y0)
2.基础知识
2.1 特殊常量表示
| 常量符号 | 说明 |
|---|---|
| i或j | 虚数单位 |
| Inf或inf | 正无穷大 |
| NaN | 不定式 |
| pi | Π |
| eps | 容量变差 |
| realmin、reamzx | 最小浮点数和最大 |
2.2 基本数值类型转换
| 类型 | 有无符号 | 转换函数 | 说明 |
|---|---|---|---|
| 整数 | 有 | intx() x表示bit | int8(36524) |
| 整数 | 无 | uintx() | |
| 双精度浮点数 | 有 | double | 存储大小8B |
| 单精度浮点数 | 有 | single | 4B |
| 复数 | complex(x) | 返回x的等效复数 | |
| 复数 | complex(a,b) | 通过两个实数a,b创建复数 z=a+bi | |
| 逻辑类型 | logical() | 返回0或1表示false或true |
2.3 结构体类型
概念:根据属性名组织起来的不同类型数据的集合;
- 结构体的任何属性都可以包含任意一种数据类型;
结构体的构造 :
- 利用赋值语句
>> man.name = 'nini';
>> man.age = 65;
>> man.salary=[123456];
>> man
man =
包含以下字段的 struct:
name: 'nini'
age: 65
salary: 123456
- 采用struct函数
>> human = struct('name',{'tina','longjie'},'age',{18,20})
human =
包含以下字段的 1×2 struct 数组:
name
age
2.4 单元数组类型
概念: 每个元素都为一个单元的数组,每个单元可以包含任意数据类型的数组;
单元数组类型构造:
- 左标志
把单元标志{}放左边 - 右标志
把单元标志{}放右边
#左标志
>> c{1,1}='coco';
>> c{1,2}=@cos;
>> c{2,1}=eye(1,2);
>> c{2,2}=false;
>> c
c =
2×2 cell 数组
{'coco' } {@cos}
{1×2 double} {[ 0]}
#右标志
c(1,1)={'coco'};
单元数组和结构体的区别和联系:
- 共同点:分级存储不同类型数据;
- 组织数据方式不同,结构体通过属性名引用,单元数组通过下标引用;
2.5 函数句柄
概念:间接调用函数数据类型
说明:就相当于给别的函数另起了一个名字;
>> f1 = @sin
f1 =
包含以下值的 function_handle:
@sin
>> f1(30)
ans =
-0.9880
>> sin(30)
ans =
-0.9880
2.6 矩阵算术运算符
| 运算符 | 用法 | 说明 |
|---|---|---|
| +、- | A+B | 矩阵加减,AB必修是长度相同的矩阵 |
| * | A*B | 矩阵乘法,AB必修是长度相同的矩阵 |
| .* | A.*B | 元素乘法,AB对应的元素相乘 |
| .^ | A.^B | 元素乘方 |
| .’ | A.’ | 转置,当矩阵为复数,不求矩阵共轭转置 |
| ’ | A’ | 转置,当矩阵为复数,求矩阵共轭转置 |
3.向量与矩阵
3.1 向量
1.概念
有方向的量,由n个数组成的有序数组;
2.向量的创建
- 直接输入法:逗号、空格创建行向量,分号创建列向量;
向量名 = [a1,a2,a3,…] - 冒号表示法 :可以设置步长;
向量名 = a1:step:an
a1:step:an==第一个元素:步长变化:最后一个元素的限定值; - 函数法:linspace、logspace;
linspace:实现线性等分 :linspace(首元素,末元素,向量元素个数)
logspace:实现对数等分: logspace(首元素的幂,尾幂,向量维数)
3.向量的运算
-
加减乘除
维数和方向相同的向量之间可以相加减;
标量可以之间和向量乘除; -
点积运算
概念:参与运算的两向量对应位置元素相乘,再将乘积相加;
注意:向量点积运算结果是标量而非向量;
函数:dot(A,B)
>> a=[1 2 2];
>> b=[1,5,9];
>> dot(a,b)
ans =
29
>> dot(a',b)
ans =
29
- 叉积运算
概念:参与运算的两向量的叉积结果也是向量且垂直于两个向量觉得的平面;
函数:cross(A,B)
>> cross(a,b)
ans =
8 -7 3
- 混合积运算
概念:实现点积和叉积的混合运算;
3.2 矩阵
1.矩阵概念
matlab中矩阵主要由二维数组表示;
可以存储和访问大量数据,矩阵单元可以存储多个类型的数据;
2.矩阵的构造
- 简单矩阵构造
方法:使用矩阵构造符“[ ]”,不同行或列用分号隔开;
>> a=[1,1,5;2,9,6;6,5,7]
a =
1 1 5
2 9 6
6 5 7
- 特殊矩阵构造
方法:函数
| 函数名 | 用途 | 说明 |
|---|---|---|
| ones | 生成全为1的矩阵 | ones(n),one(n,m) |
| zeros | 生成全为0的矩阵 | … |
| eye | 生成单位矩阵(主对角线全为1,其他为0) | … |
| diag | 吧向量转化为对角矩阵 | … |
| magic | 生成魔方矩阵 | 每行每列之和相等 |
| rand | 生成0~1均匀分布的随机数 | magic(n) |
| randn | 生成均值0,方差1高斯分布的随机数 | … |
| randperm | 生成整数为1~n的随机排列 | n |
| compan | 生成多项式的伴随矩阵 |
- 矩阵的操作
- 合并: c=[a b]水平方向合并;c=[a;b]垂直方向
| 函数 | 操作 | 说明 |
|---|---|---|
| cat | 指定方向合并 | cat(1,a,b)竖直合并、cat(2,a,b)水平合并 |
| horzcat | 水平方向合并 | horzcat(a,b) |
| vertcat | 竖直方向合并 | |
| repmat | 复制矩阵构造新矩阵 | repmat(a,m,n):m*n个a的大矩阵 |
- 拓展
直接输入位置 其他补0
a =
1 1 5
2 9 6
6 5 7
>> a(4,4)=100
a =
1 1 5 0
2 9 6 0
6 5 7 0
0 0 0 100
- 删除
位置=【】
>> a(4,:)=[]
a =
1 1 5 0
2 9 6 0
6 5 7 0
3.矩阵信息获取
| 函数名 | 说明 | 示例 |
|---|---|---|
| length | 最长方向长度 | |
| ndims | 维度 | |
| numel | 矩阵元素个数 | |
| size | 矩阵各方向长度 |
4.矩阵结构改变
| 函数名 | 说明 | 示例 |
|---|---|---|
| reshape | 指定行列排列矩阵元素 | b=reshape(a,m,n) |
| repmat | 指定行列复制矩阵 | b=repmat(a,m,n) |
| rot90 | 旋转矩阵90° | |
| fliplr | 以竖直方向为轴做镜像 | |
| flipud | 以水平方向为轴做镜像 | |
| flipdim | 以指定的轴做镜像 | |
| transpose | 矩阵转置 | |
| ctranspose | 矩阵的共轭转置 |
5.稀疏矩阵
- 函数:sparse()从满矩阵转换成稀疏矩阵;
A =
0 0 5 0
8 0 0 0
0 1 0 0
0 0 0 7
>> sparse(A)
ans =
(2,1) 8
(3,2) 1
(1,3) 5
(4,4) 7
4.矩阵运算
4.1 矩阵分析函数
| 函数名 | 说明 | 函数名 | 说明 |
|---|---|---|---|
| norm | 求矩阵或向量的范数 | null | 矩阵的零空间 |
| normest | 估计矩阵的二阶范数 | orth | 矩阵的正交空间 |
| rank | 矩阵的秩(对角元素的和) | rref | 矩阵的约化行阶梯形式 |
| trace | 矩阵的迹 | subspace | 两个矩阵空间的夹角 |
| det | 矩阵的行列式 |
1. 范数
-
概念: 存在一个函数r(x),x为线性空间的向量,满足:
r(x)>0,且r(x)=0的充要条件是x=0;
r(ax)=ar(x);
r(x+y)<=r(x)+r(y); -
函数:norm()
-
范例
>> a = [5 -2 -2];
>> norm(a)
ans =
5.7446
2. 矩阵的秩
- 概念: 矩阵中线性无关的列(行)向量的个数称为列(行)秩,行秩==列秩;
- 函数 :rank()
- 范例
>> a=eye(6)
a =
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
>> rank(a)
ans =
6
3.矩阵的行列式
- 概念: 矩阵行列式是指矩阵的全部元素构成的行列式;
- 函数 :det()
- 范例
a =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
>> det(a)
ans =
5.133671265866724e-13
4. 矩阵的迹
- 概念: 对角元素之和
- 函数 trace()
- 范例
a =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
>> trace(a)
ans =
34
4.2 线性方程组
- 概念 :给定两个矩阵A、B,是否存在唯一解使得AX=B或XA=B;
- 求解线性方程的解方法 :”\“,“/”
X=A\B %求AX=B的解;
X=B/A %求XA=B的解;
1.一般解的过程
- 解相应AX=0,得到基础解 //函数:null(A)
- 求非齐次线性方程组AX=B,得到特殊解;
- 结果为基础解的线性组合加上特殊解;
2.恰当方程组求解
3.超定方程组求解
- 概念:方程个数大于未知量的个数的方程组
4.3 矩阵的特征值和特征向量
概念 :Av = λv
v:特征向量
λ:特征值
函数 :eig()
>> A = [3 15 27;1 8 32;-4 -12 -38];
>> [V D] = eig(A)
V =
1 至 2 列
-0.308989048325970 + 0.000000000000000i 0.804242095017848 + 0.000000000000000i
-0.661741507195511 + 0.000000000000000i -0.071797479267306 + 0.558020092765743i
0.683098781779930 + 0.000000000000000i -0.085725506688215 - 0.171185537195533i
3 列
0.804242095017848 + 0.000000000000000i
-0.071797479267306 - 0.558020092765743i
-0.085725506688215 + 0.171185537195533i
D =
1 至 2 列
-24.565845929723153 + 0.000000000000000i 0.000000000000000 + 0.000000000000000i
0.000000000000000 + 0.000000000000000i -1.217077035138431 + 4.660651202451104i
0.000000000000000 + 0.000000000000000i 0.000000000000000 + 0.000000000000000i
3 列
0.000000000000000 + 0.000000000000000i
0.000000000000000 + 0.000000000000000i
-1.217077035138431 - 4.660651202451104i
5.数据绘图
5.1二维图形绘制
二维绘图第三个基本命令:plot \fplot\ezplot
1. plot二维绘图命令
- 概念:plot函数将从外部输入或通过函数数值计算得到数据矩阵转换成连线图;
- 格式 :plot(y), plot(x,y), plot(x,y,s);
plot(y)命令: 参数y可以是向量、实数矩阵、复数向量;
eg1:绘制向量曲线
>> x = 0:pi/100:2*pi;
>> y = sin(x);
>> plot(y)
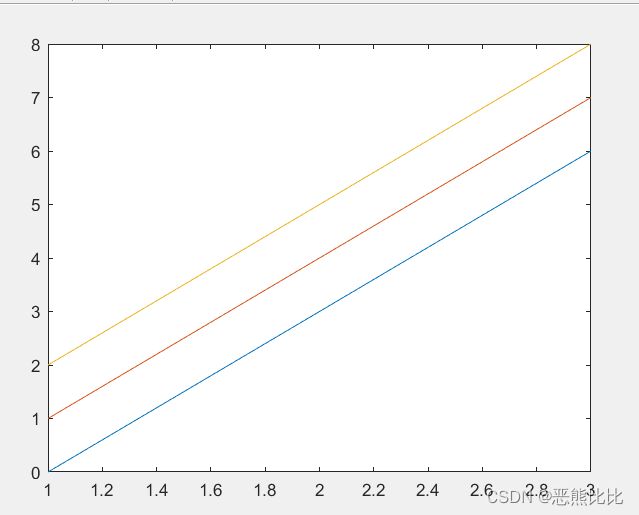
>> y = [0 1 2;3 4 5;6 7 8];
>> plot(y)
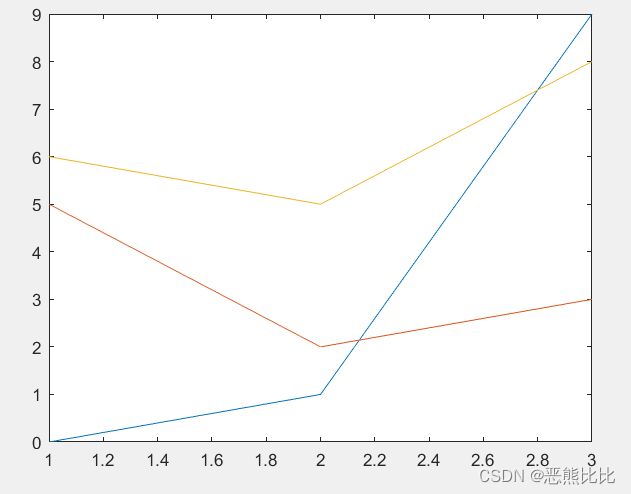
>> y = [0 5 6;1 2 5;9 3 8];
>> plot(y)
eg3:绘制复数向量曲线
>> x = [1:0.5:10];
>> y = [1:0.5:10];
>> z=x+y.*i;
>> plot(y)
plot(x,y)命令: 参数x,y可以是向量、实数矩阵、复数向量;
eg1:绘制双向量曲线
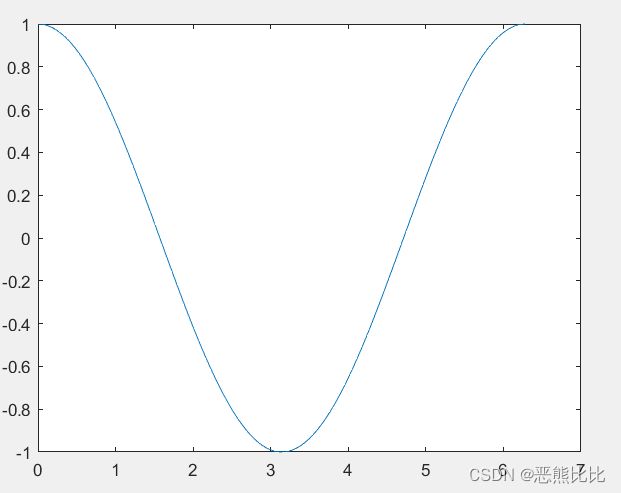
>> x=0:pi/100:2*pi;
>> y=cos(x);
>> plot(x,y)
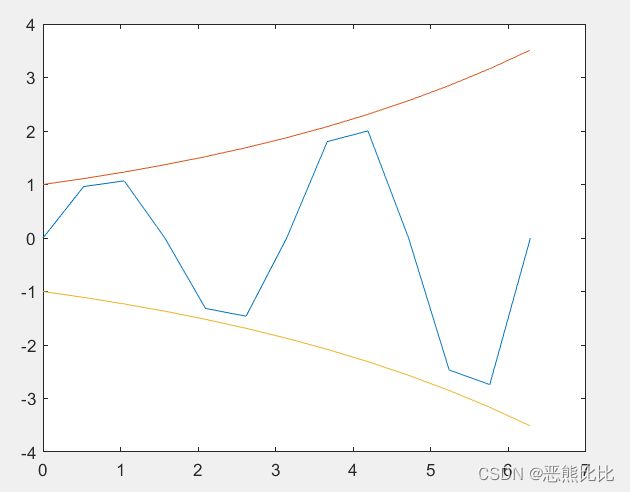
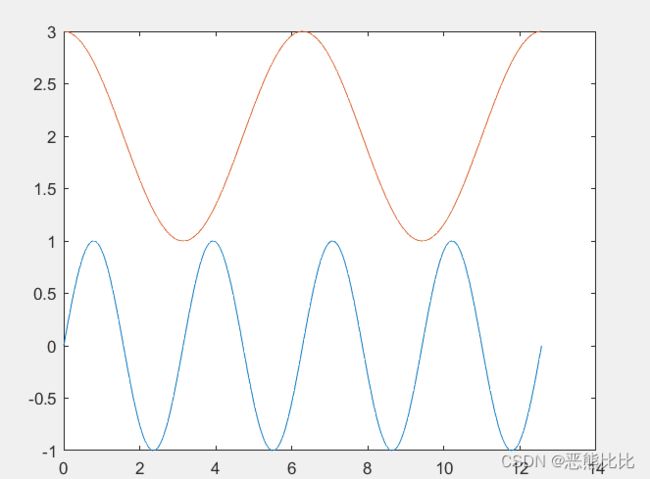
eg2:绘制向量矩阵曲线;
>> x=0:pi/100:4*pi;
>> y=[sin(2*x);cos(x)+2];
>> plot(x,y)
>>
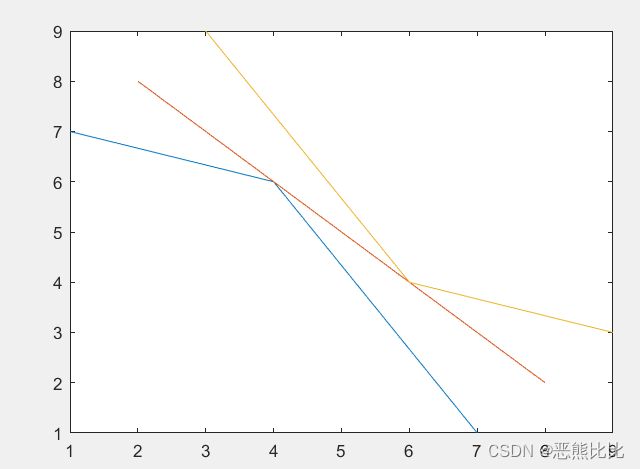
eg3:双矩阵曲线;
>> x=[1 2 3;4 5 6;7 8 9];
>> y=[7 8 9;6 5 4;1 2 3];
>> plot(x,y)
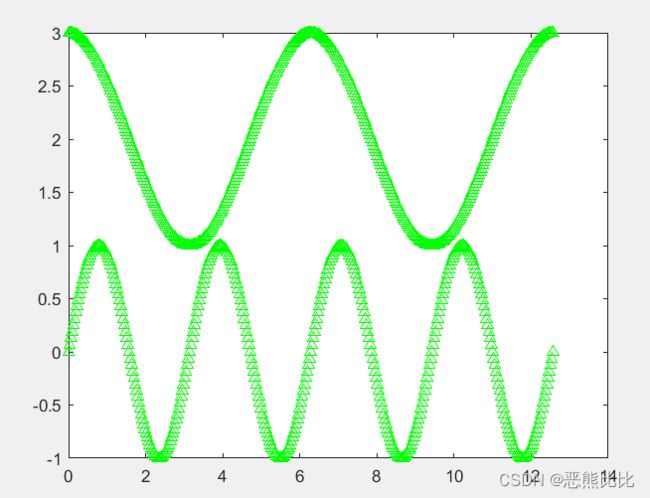
plot(x,y,s)命令: 用于绘制不同线形,标记和颜色的图形;
//s为字符:可以代表不同的线形,标记和颜色
>> x=0:pi/100:4*pi;
>> y=[sin(2*x);cos(x)+2];
>> plot(x,y,'g^')
2.多次叠图hold命令
若是已存在图形窗口中用plot函数继续添加新的图形内容,则可以使用图形保持命令hold;
执行hold on 命令,再执行plot命令,可以在保存原图基础上添加新图;
执行hold off命令关闭此功能;
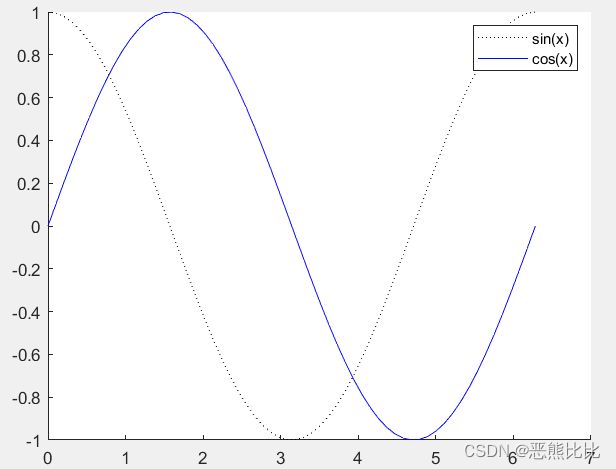
>> x= linspace(0,2*pi,60);
>> y=sin(x);
>> z=cos(x);
>> plot(x,y,'b');
>> hold on;
>> plot(x,z,'k:');
>> legend('sin(x)','cos(x)');
>> hold off;
3.多子图suplot命令
suplot(m,n,k)函数,可以在视图中显示多个子图;
m*n表示子图个数;
k表示当前图;
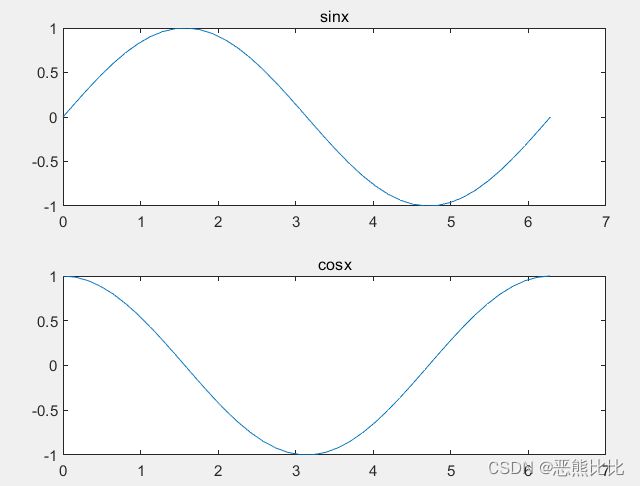
>> x= linspace(0,2*pi,40);
>> y=sin(x);
>> z=cos(x);
>> subplot(2,1,1);
>> plot(x,y);
>> title('sinx');
>> subplot(2,1,2);
>> plot(x,z);
>> title('cosx');
4.fplot 二维绘图命令
fplot可以自定义自变量取值间隔,当函数变换慢时间隔大一点,函数变化快时间隔小一点;
5.ezplot 二维绘图命令
ezplot用于绘制在某一自变量区域内的图形命令;
6.二维特殊图形函数
| 函数名 | 说明 |
|---|---|
| pie | 饼状图 |
| barh | 水平条形图 |
| bar | 垂直条形图 |
| area | 填充图 |
| scatter | 离散图 |
| gplot | 拓扑图 |
| stairs | 阶梯图 |
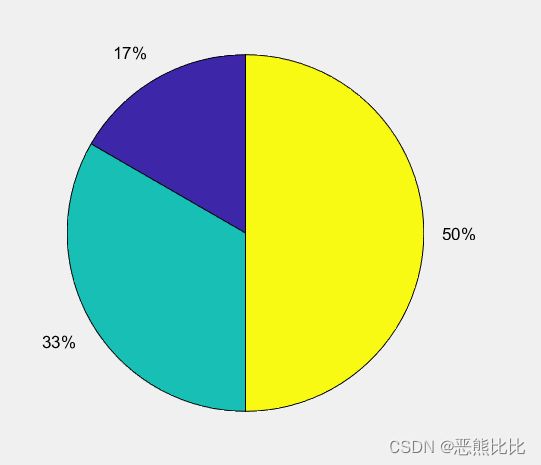
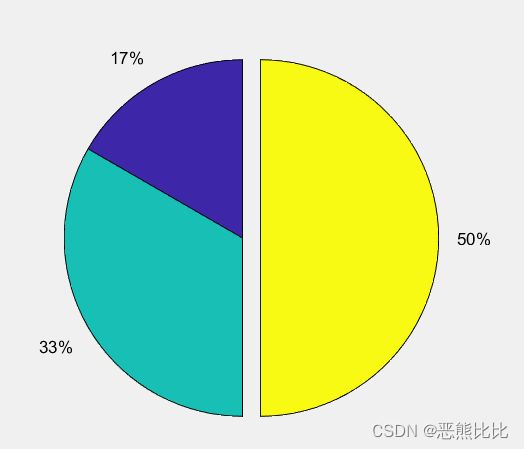
eg:pie
>> x = [1,2,3];
>> pie(x)
>> x = [1,2,3];
>> y = [0,0,1];
>> pie(x,y)
5.2三维数组绘图
三维绘图函数
| 函数 | 说明 |
|---|---|
| plot3 | 基本函数,三个数据参数 |
| mesh | 绘制三维网格图 |
| surf | 绘制着色的三维曲面图 |
| meshgrid | 将给定的区域按一定的方式平分成网格 |
| meshc | 用mesh命令绘制的三维网格中绘制出等高线 |
| meshz | 增加绘制边界功能 |
| surfc | 绘制底层高等先 |
| surfl | 绘制光照效果 |
1.plot3(x,y,z)
plot3(x,y,z) #绘制三维空间坐标
plot3(x,y,z,LineSpec) #增加指定线形、标记、颜色
plot3(x1,y1,z1,...xn,yn,zn)
plot3(x1,y1,z1,LineSpace1.....)
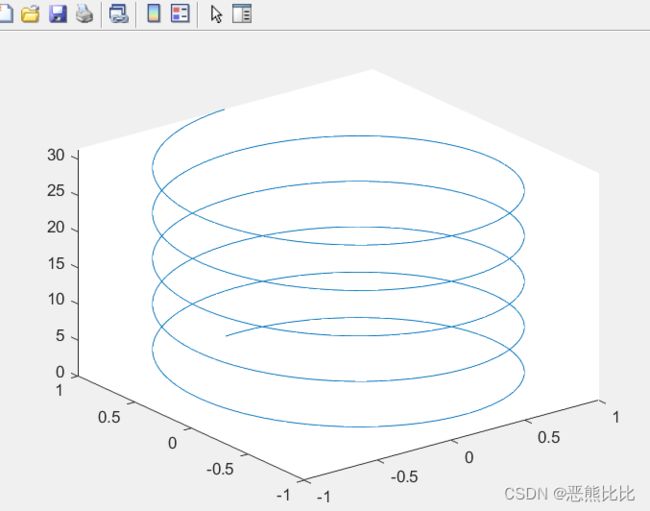
eg1:绘制螺旋线
>> t = 0:pi/50:10*pi;
>> plot3(sin(t),cos(t),t)
>>
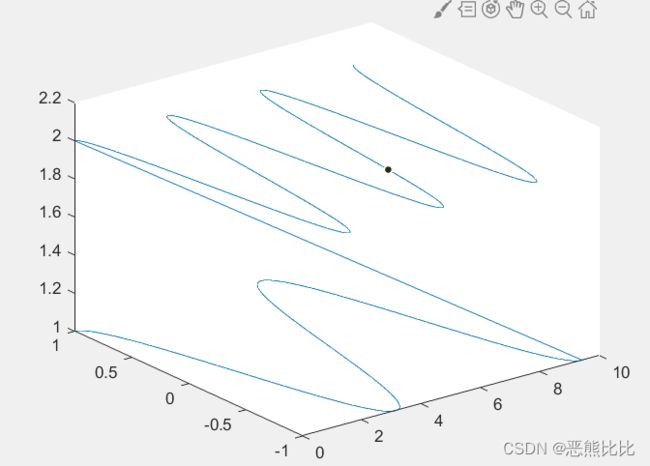
t = [0:pi/100:3*pi];
>> x=[t t];
>> y = [cos(t) cos(2*t)];
>> z=[sin(t).^2+(cos(t)).^2 (sin(t)).^2+(cos(t)).^2+1];
>> plot3(x,y,z)
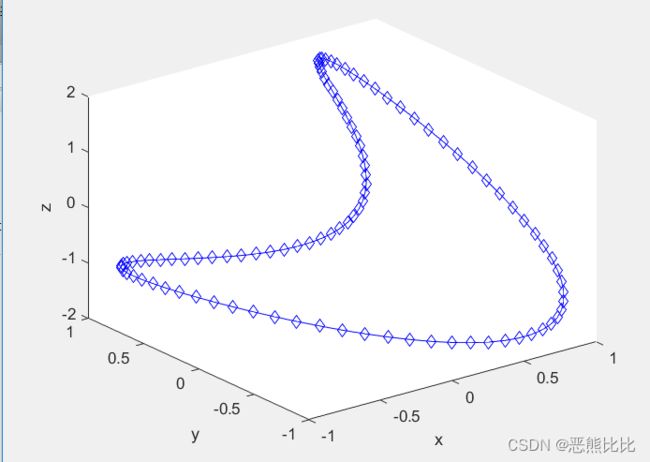
eg3:通过三维曲线图演示该曲线的参数方程
>> t = (0:0.02:2)*pi;
>> x = sin(t);
>> y = sin(2*t);
>> z = 2*cos(t);
>> plot3(x,y,z,'b-',x,y,z,'bd')
>> xlabel('x'),ylabel('y'),zlabel('z')
2.mesh()
mesh绘制三维网格图
用xy平面上的z坐标定义一个网格面;
通过相邻点用直线连接而构成一个网格图;
mesh(x,y,z) #创建网格图,有实色边颜色,无面颜色;
mesh(z) #创建网格图,将z中元素的列索引和行索引作x坐标和y坐标;
mesh(———,c) #指定边颜色
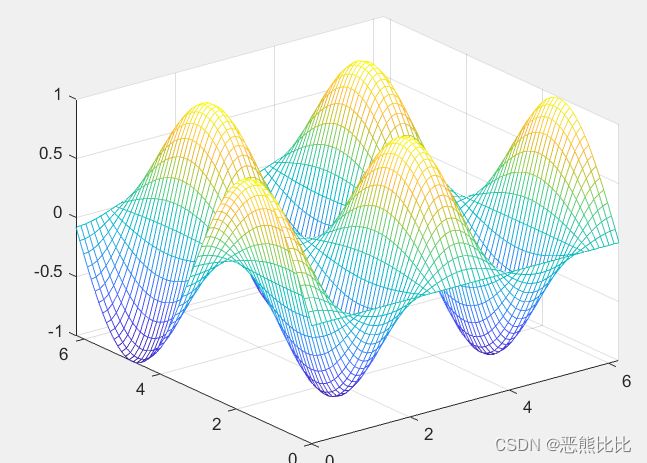
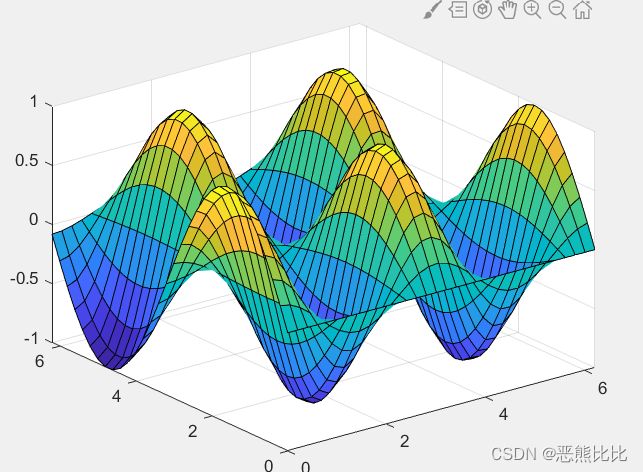
eg1:绘制三维网格图
>> x = 0:0.1:2*pi;
>> y = 0:0.1:2*pi;
>> z = sin(x')*cos(2*y);
>> mesh(x,y,z)
>>
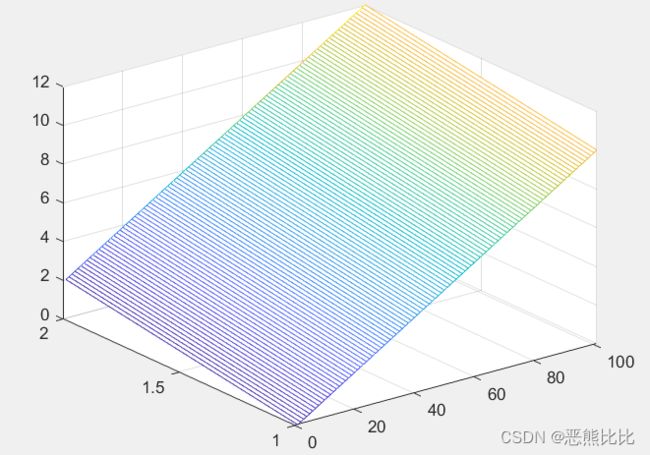
eg2:绘制三维网格图
>> z = [0:0.1:10;2:0.1:12];
>> mesh(z)
3. surf()
绘制着色的三维曲面
surf(x,y,z) #创建一个具有实色边和实色面的三维曲面
surf(x,y,z,c) #c指定曲面颜色
surf(z) #将z中元素的行列索引作为y、x坐标
surf(z,c)
surf(ax,__) #将图形绘制到ax指定的坐标区域
eg:绘制着色三维曲面
>> x=0:0.2:2*pi;
>> y=0:0.2:2*pi;
>> z=sin(x')*cos(2*y);
>> surf(x,y,z)
6.图形处理
6.1 图形标识
1.坐标轴
2.图形标注
坐标轴与图形标注的主要函数:
| 函数名 | 说明 |
|---|---|
| xlable | x轴 |
| ylable | |
| zlable | |
| title | 标题 |
>> x = 0:0.1*pi:3*pi;
>> y = 2*cos(x);
>> plot(x,y)
>>> xlabel('x(0-3\pi)','fontweight','bold');
>> ylabel('y(0-2)','fontweight','bold');
>> title('y=2*cosx')
>>
3.图形文本标注 text、gtext
| 函数名 | 说明 |
|---|---|
| text | 定义用于注释的文本字符串和放置注释的位置; |
| gtext | 用鼠标选择注释文字的位置 |
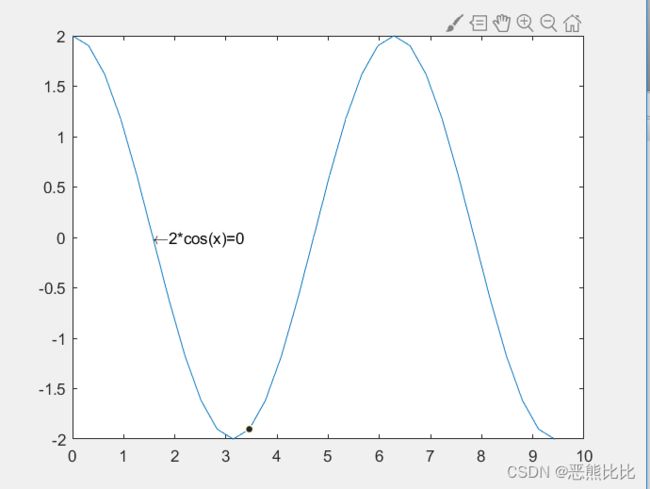
>> x = 0:0.1*pi:3*pi;
>> y = 2*cos(x);
>> plot(x,y)
>> text(pi/2,2*cos(pi/2),'\leftarrow2*cos(x)=0','FontSize',10)
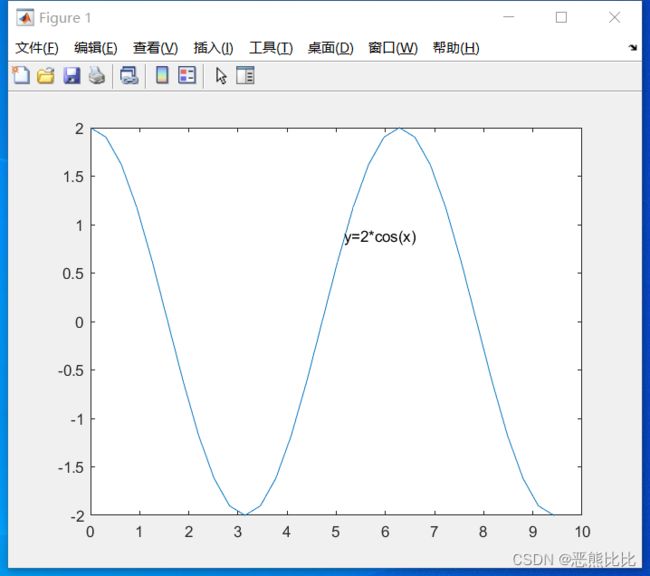
>> x = 0:0.1*pi:3*pi;
>> y = 2*cos(x);
>> plot(x,y)
>> gtext('y=2*cos(x)','FontSize',10)
4.图例标注 legend
当绘制多条曲线时,可以使用legend 添加图例进行区别
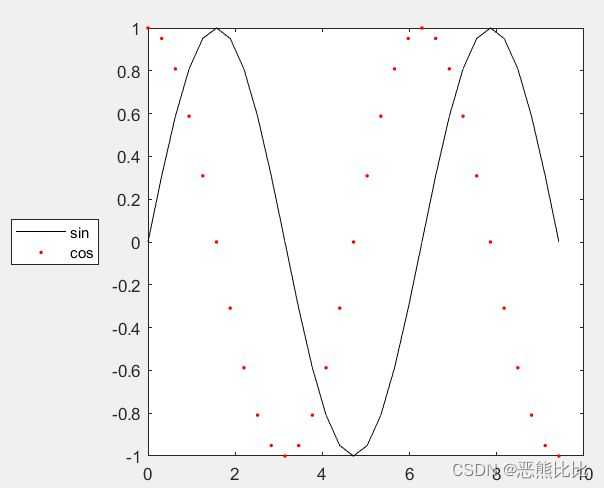
>> x = 0:0.1*pi:3*pi;
>> y1=sin(x);
>> y2=cos(x);
>> plot(x,y1,'k-',x,y2,'r.')
>> legend('sin','cos','Location','WestOutside')
>>
6.2图形控制
1.图形数据取点 ginput
ginput可以方便的通过鼠标读取二维平面图中任意一点坐标;
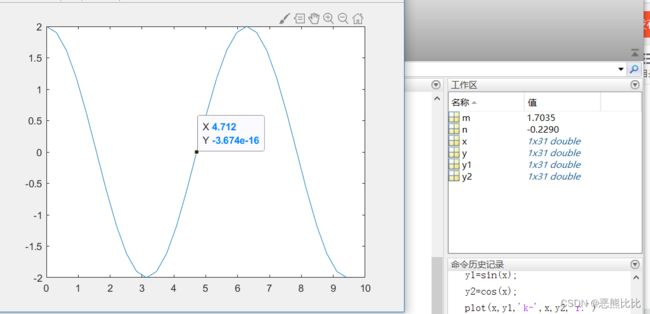
>> x = 0:0.1*pi:3*pi;
>> y=2*cos(x);
>> plot(x,y)
>> [m,n] = ginput(1)
2.坐标轴控制 axis、grid、box、zoom
| 函数 | 说明 | 作用 |
|---|---|---|
| axis | 坐标特征控制函数 | 控制坐标轴的刻度范围及显示形式 |
| grid | 坐标网格绘制函数 | 用于绘制坐标网格 |
| box | 坐标轴封闭控制函数 | 用于在图形四周显示坐标 |
| zoom | 坐标轴缩放控制函数 | 实现对二维图形的缩放 |
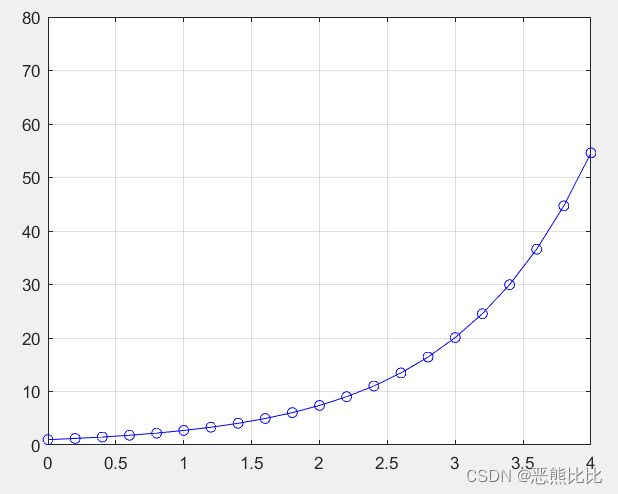
axis:
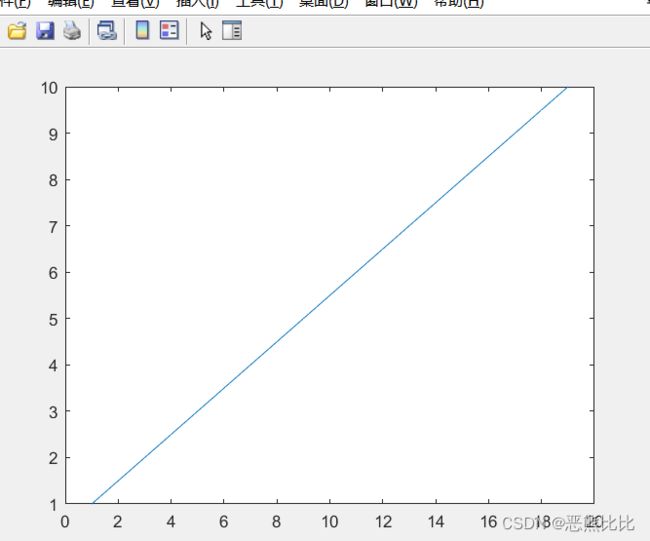
#未设定前
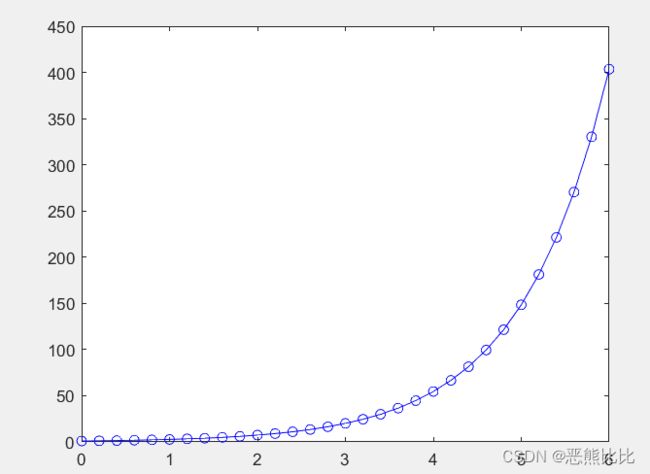
>> x=0:0.2:6;
>> plot(x,exp(x),'-bo')
>
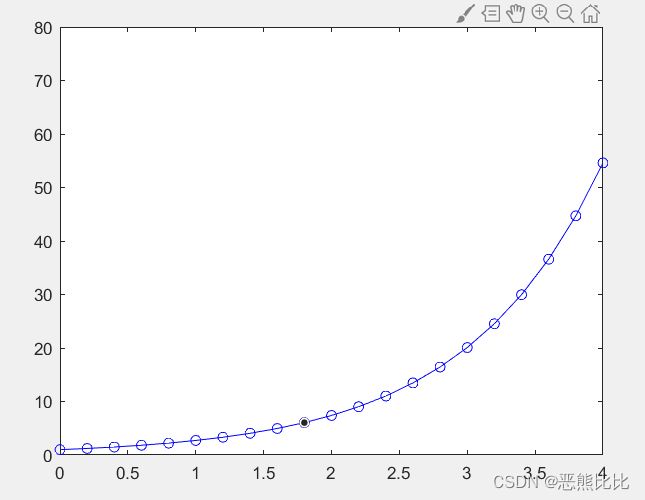
>#设置后
>>> axis([0 4 0 80])
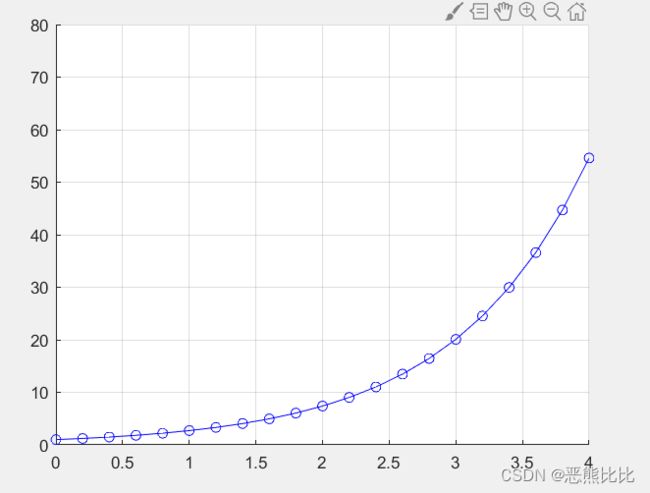
grid:
>> x=0:0.2:6;
>> plot(x,exp(x),'-bo')
>> axis([0 4 0 80])
>>
>> grid on #添加
>> grid off
box on #将封闭网格打开
box off
3.视角与透视控制 view、hidden
view:用于指定立体图形观察点;
hidden 查看被隐藏的网格
7.程序设计
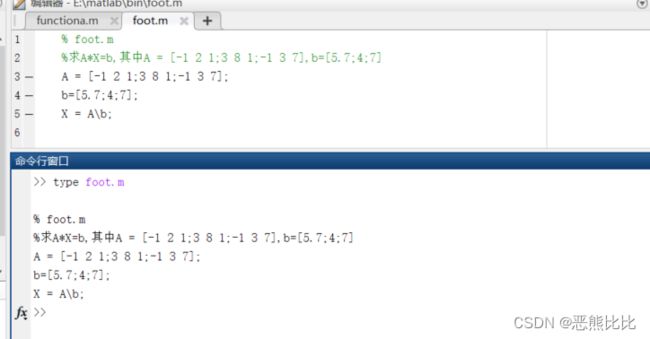
7.1 M文件
M文件就是以.m为扩展名的文本文件,不能进入命令行窗口,由文本编译器创建外部文件。
M文件有两种格式:函数、脚本;
- 函数
前言:Matlab是由C语言开发而成的,所有M文件的语法规则和C几乎一样。
函数结构:
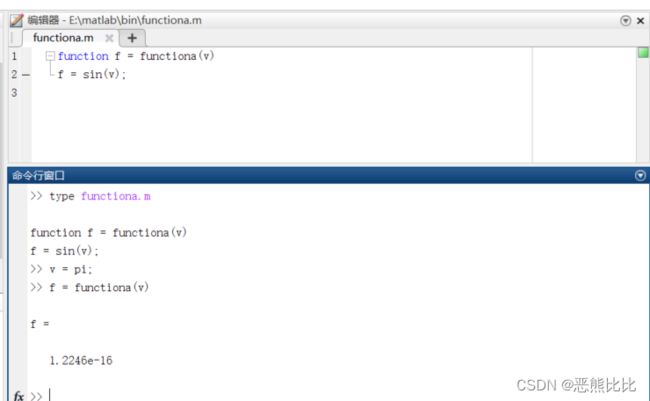
#创建一个名为functiona.m的文件
function f = functiona(v)
f = sin(v);
- 脚本
脚本中包含matlab的各种命令,与批处理文件相似,在matlab命令行中直接输入此文件的主文件名,matlab可以逐一执行此文件内所有命令;
%脚本式m文件运行生成的所有变量都是全局变量,运行脚本后,生成的所有脚本变量都驻留在matlab基本工作空间内
7.2函数语句
1.顺序语句
>> a=3;
>> b=5;
>> c=a*b
c =
15
2.循环语句
>> for i=1:3
for j=1:2
a(i,j)=i+j;
end
end
>>
>> disp(a)
2 3
3 4
4 5
3.代码编写
书写代码
A = [5 6 0 0 0
1 5 6 0 0
0 1 5 6 0
0 0 1 5 6
0 0 0 1 5];
B = [1 0 0 0 1]';
R_A = rank(A) %求秩
X = A\B %求解
运行
>> linerequ
R_A =
5
X =
2.2662
-1.7218
1.0571
-0.5940
0.3188
8. 数值计算
8.1 求解线性方程组
| 矩阵函数 | 说明 |
|---|---|
| rank() | 求秩 |
| det() | 求行列式 |
| inv() | 求逆矩阵 |
| pinv() | 求伪逆 |
| trance() | 求迹,对角线元素和 |
1.直接法
>> A = [1 3 -3 -1;3 -6 -3 4;1 5 -9 -8];
>> B = [1 0 4]';
>> X = A\B
X =
0
-0.0000
-0.2667
-0.2000
2.逆矩阵法
>> A=[1 2;3 4];
>> B = [-1;-1];
>> x=A^-1*B
x =
1.0000
-1.0000
3.Lu分解
>> A = [4 2 -1;3 -1 2;11 3 1];
>> B = [2 10 8]';
>> D = det(A)
D =
-10.0000
>> [L,U] = lu(A)
L =
0.3636 -0.5000 1.0000
0.2727 1.0000 0
1.0000 0 0
U =
11.0000 3.0000 1.0000
0 -1.8182 1.7273
0 0 -0.5000
>> X=U\(L\B)
X =
4.0000
-10.0000
-6.0000
>>
8.2 函数计算、数据分析、微分方程、积分方程
方法:数值逼近法
1.插值
插值问题:为给定表格函数构造相适应的近似解析表达式;
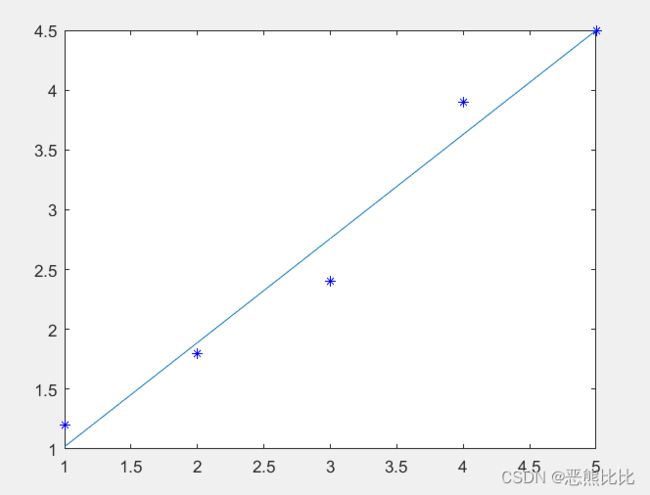
2.曲线拟合
eg:在某实验中测得数据,已知x和y呈线性关系,y=kx+b,求系数k和b;
x:1,2,3,4,5
y:1.2,1.8,2.4,3.9,4.5
>> x=[1,2,3,4,5];
>> y=[1.2,1.8,2.4,3.9,4.5];
>> [p,s]=polyfit(x,y,1)
p =
0.8700 0.1500
s =
包含以下字段的 struct:
R: [2×2 double]
df: 3
normr: 0.4930
>> y1=polyval(p,x);
>> plot(x,y,'b*');
>> hold on;
>> plot(x,y1)