YOLOv5的Tricks | 【Trick6】学习率调整策略（One Cycle Policy、余弦退火等）

---

如有错误，恳请指出。

---

对于学习率的调整一直是个比较困难的问题， 在yolov5中提供了两种学习率的调整方式，一种是线性调整，另外一种就是One Cycle Policy。而在查找资料的过程中，了解到了其他的学习率调整策略，这里一并归纳到这篇笔记中。

其中包括：LR Range Test、Cyclical LR、One Cycle Policy、SGDR、AdamW 、SGDW、pytorch实现的余弦退火策略。具体的学习率调整策略，详细见参考资料。

---

0. Yolov5的学习率调整方案

yolov5代码中提供了两种学习率调整方案：线性学习率与One Cycle学习率调整

代码比较简单，如下所示：

# Scheduler
if opt.linear_lr:
    lf = lambda x: (1 - x / (epochs - 1)) * (1.0 - hyp['lrf']) + hyp['lrf']  # linear
else:
    lf = one_cycle(1, hyp['lrf'], epochs)  # cosine 1->hyp['lrf']
scheduler = lr_scheduler.LambdaLR(optimizer, lr_lambda=lf)  # plot_lr_scheduler(optimizer, scheduler, epochs)

配合辅助绘制函数plot_lr_scheduler，这里可以将两种学习率调整策略的学习率随epochs变化绘制出来，这里我重新写了一个函数比较方便调用lf。

参考代码：

def plot_lr_scheduler(optimizer, scheduler, epochs=300, save_dir=''):
    # Plot LR simulating training for full epochs
    optimizer, scheduler = copy(optimizer), copy(scheduler)  # do not modify originals
    y = []
    for _ in range(epochs):
        scheduler.step()
        y.append(optimizer.param_groups[0]['lr'])
    plt.plot(y, '.-', label='LR')
    plt.xlabel('epoch')
    plt.ylabel('LR')
    plt.grid()
    plt.xlim(0, epochs)
    plt.ylim(0)
    plt.savefig(Path(save_dir) / 'LR.png', dpi=200)
    plt.close()

# 功能: 绘制在学习率调整方法lr下, 学习率随epoch的曲线
def plot_lr(lf, epochs=30):
	# load model
    weight = r"./runs/train/mask/weights/last.pt"
    device = torch.device('cpu')
    ckpt = torch.load(weight, map_location=device)
    model = Model(ckpt['model'].yaml, ch=3, nc=3, anchors=None).to(device)
    model.load_state_dict(ckpt['model'].state_dict())
	
	# optimizer 
    g0, g1, g2 = [], [], []  # optimizer parameter groups
    for v in model.modules():
        if hasattr(v, 'bias') and isinstance(v.bias, nn.Parameter):  # bias
            g2.append(v.bias)
        if isinstance(v, nn.BatchNorm2d):  # weight (no decay)
            g0.append(v.weight)
        elif hasattr(v, 'weight') and isinstance(v.weight, nn.Parameter):  # weight (with decay)
            g1.append(v.weight)

    optimizer = SGD(g0, lr=0.01, momentum=0.937, nesterov=True)
    optimizer.add_param_group({'params': g1, 'weight_decay': 0.0005})  # add g1 with weight_decay
    optimizer.add_param_group({'params': g2})  # add g2 (biases)

    scheduler = lr_scheduler.LambdaLR(optimizer, lr_lambda=lf)
    plot_lr_scheduler(optimizer, scheduler, epochs, save_dir='./runs/test')
    print('plot successes')

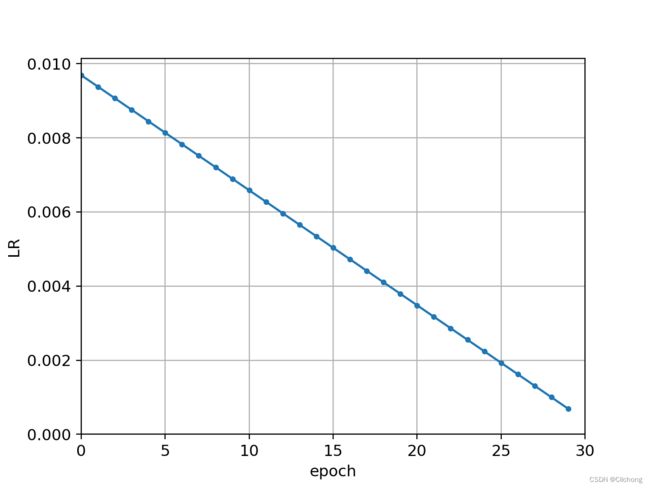
下面利用以上函数分别查看线性学习率与One Cycle的学习率变化曲线

• 线性学习率变化曲线

绘制曲线代码：

if __name__ == '__main__':
    epochs = 30
    lrf = 0.1 
    lf = lambda x: (1 - x / (epochs - 1)) * (1.0 - lrf) + lrf 
    plot_lr(lf, epochs)

学习率曲线图：

• OneCycle学习率变化曲线

绘制曲线代码：

def one_cycle(y1=0.0, y2=1.0, steps=100):
    # lambda function for sinusoidal ramp from y1 to y2 https://arxiv.org/pdf/1812.01187.pdf
    return lambda x: ((1 - math.cos(x * math.pi / steps)) / 2) * (y2 - y1) + y1

if __name__ == '__main__':
    epochs = 30
    lf = one_cycle(1, 0.1, 30)  # cosine 1->hyp['lrf']
    plot_lr(lf, epochs)

学习率曲线图：

分析：One Cycle的学习率变化过程是从lr0=0.01呈余弦变化衰退到lr0*lrf = 0.01*0.1 = 0.001上。在了解完下诉的one cycle，就可以侧面从yolov5的学习率变化曲线可出，其不完全是按照One Cycle Policy图像来设置的，更偏向于普通的余弦退火策略。

下面的内容就是对各种学习率调整方法进行理论分析介绍与归纳。

---

1. LR Range Test

2015年，Leslie N. Smith提出了该技术。其核心是将模型进行几次迭代，在最初的时候，将学习率设置的足够小，然后，随着迭代次数的增加，逐渐增加学习率，记录下每个学习率对应的损失，并绘图：（LR 的初始值仅为 1e-7，然后增加到 10）

LR Range Test 图应该包括三个区域，第一个区域中学习率太小以至于损失几乎没有减少，第二个区域里损失收敛很快，最后一个区域中学习率太大以至于损失开始发散。因此，第二个区域中的学习率范围就是我们在训练时应该采用的。

所以，这个方法字如其名，就是学习率范围测试，为训练寻找一个合适的学习率范围。

---

2. Cyclical LR

在一些经典方法中，学习率总是逐步下降的，从而保证模型能够稳定收敛，但Leslie Smith对此提出了质疑，Leslie Smith认为让学习率在合理的范围内周期性变化（即Cyclical LR： 在 lr 和 max_lr 范围内循环学习率）是更合理的方法，能够以更小的步骤提高模型准确率。

如上图所示，max_lr 与 lr 可以通过 LR Range test 确定，作者认为：最优学习率将在处于这个范围内，所以如果学习率在这个区间变化，大多数情况下你将得到一个接近最优学习率的学习率。

总结：

1. Cyclical LR是一种有效避开鞍点的方法，因为在鞍点附近梯度较小，通过增加学习率可以让模型走出困境。
2. Cyclical LR能够加速模型训练过程
3. Cyclical LR在一定程度上可以提高模型的泛化能力（将模型带入平坦最小值区域）

---

3. One Cycle Policy

在Cyclical LR和LR Range Test的基础上，Leslie 继续改进，提出了The 1cycle policy。即周期性学习率调整中，周期被设置为1。在一周期策略中，最大学习率被设置为 LR Range test 中可以找到的最高值，最小学习率比最大学习率小几个数量级（比如设为最大值的0.1倍）。

如上图，一整个训练周期约400个iter，前175个iter用来warm-up，中间175个iter用来退火到初始学习率，最后几十个iter学习率进行进一步衰减。我们将上述三个过程称为三个阶段。

1. 第一阶段：线性warm-up：其效果与一般的warm-up效果类似，防止冷启动导致的一些问题。
2. 第二阶段：线性下降至初始学习率：由于第一、第二阶段中有相当大的时间模型处于较高的学习率，作者认为，这将起到一定的正则化作用，防止模型在陡峭最小值驻留，从而更倾向于寻找平坦的局部最小值。
3. 第三阶段：学习率衰减至0：将使得模型在一个‘平坦’区域内收敛至一个较为‘陡峭’的局部最小值。

上图展示了一周期策略训练时，模型在训练集和验证集上的损失变化。在该图中，学习率在 0 和 41 时期之间从 0.08 上升到 0.8，在 41 和 82 时期之间回到 0.08，然后在最后几个时期达到 0.08 的百分之一。可见，在学习率较大时，验证集损失变得不稳定，但平均来看，验证集损失与训练集损失的差值没有变化太多，说明这个阶段模型学习到的知识具有较好的泛化能力（即大学习率一定程度上起到了正则化的作用）。而在训练末期，学习率不断衰减，这时训练集损失有明显下降，而验证集损失没有明显下降，两者的差值扩大了，因此，在训练末期，模型开始产生了一定的过拟合。

在这张图中，学习率在 0 和 22.5 时期之间从 0.15 上升到 3，在 22.5 和 45 时期之间回到 0.15，然后在最后几个时期达到 0.15 的百分之一。凭借非常高的学习率，我们可以更快地学习并防止过度拟合。在我们消除学习率之前，验证损失和训练损失之间的差异一直非常小。这就是 Leslie Smith 所描述的超收敛现象。使用这种技术，我们可以在 50 个 epoch 内训练一个 resnet-56，使其在 cifar10 上的准确率达到 92.3%。进入一个 70 个 epoch 的周期可以让我们达到 93% 的准确率。

• Cyclical momentum

在参考资料3中还提到了Cyclical momentum周期性动量的方法。

伴随着向更大学习率的转变， Leslie Smith 在他的实验中发现，降低动量会带来更好的结果。这支持了这样一种直觉，即在训练的那部分，我们希望 SGD 快速进入新的方向以找到更平坦的区域，因此需要赋予新的梯度更多的权重。在实践中，他建议选择 0.85 和 0.95 这样的两个值，当我们提高学习率时，从较高的值减小到较低的值，然后随着学习率的下降返回到较高的动量。如下图所示：

根据 Leslie 的说法，在整个训练期间选择的确切最佳动量值可以给我们相同的最终结果，但使用循环动量消除了尝试多个值和运行几个完整循环的麻烦，从而浪费了宝贵的时间。

• 总结：

One Cycle Policy的含义也从图也可以看见，就是学习率变化分为3个阶段但是只有一个周期，也就是称为1周期策略的学习率调整。同时也可以侧面从yolov5的学习率变化曲线可出，其不完全是按照One Cycle Policy图像来设置的，更偏向于普通的余弦退火策略。

---

4. SGDR

来源见参考资料2.

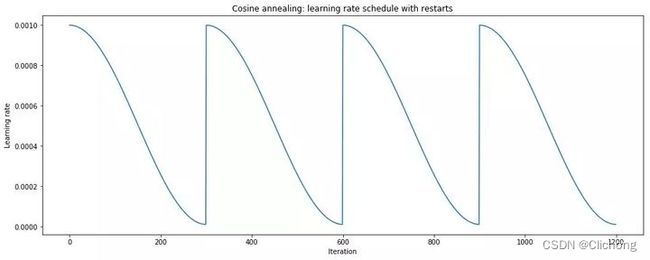
SGDR是性能良好的旧版热重启 SGD。原则上，SGDR 与 CLR 本质是非常相似的，即在训练过程中学习率是不断变化的。

其中，主动退火策略（余弦退火）与重启计划相结合。重启是一个「热」重启，因为模型没有像全新模型那样重启，而是在重新启动学习率后，使用重启前的参数作为模型的初始解决方案。这在实现中非常简单，因为你不需要对模型执行任何操作，只需要即时更新学习率。

到目前为止，Adam 等自适应优化方法仍然是训练深度神经网络的最快方法。然而，各种基准测试的许多最优解决方案或在 Kaggle 中获胜的解决方案仍然选用 SGD，因为他们认为，Adam 获得的局部最小值会导致不良的泛化。

SGDR 将两者结合在一起，迅速「热」重启到较大的学习率，然后利用积极的退火策略帮助模型与 Adam 一样快速（甚至更快）学习，同时保留普通 SGD 的泛化能力。

---

5. AdamW 、SGDW

来源见参考资料1，2.（参考资料1对这部分内容可能更详细一点）

「热」启动策略非常好，并且在训练期间改变学习率似乎是可行的。但为什么上一篇论文没有扩展到 AdamR 呢？论文《Fixing Weight Decay Regularization in Adam》的作者曾说：

虽然我们初始版本的 Adam 在「热」启动时性能比 Adam 更好，但相比于热启动的 SGD 没有什么竞争力。

作者在论文中提出了以下意见：

• L2 正则化和权值衰减不同。
• L2 正则化在 Adam 中无效。
• 权值衰减在 Adam 和 SGD 中同样有效。
• 在 SGD 中，再参数化可以使 L2 正则化和权值衰减等效。
• 主流的库将权值衰减作为 SGD 和 Adam 的 L2 正则化。

他们提出了 AdamW 和 SGDW，这两种方法可以将权值衰减和 L2 正则化的步骤分离开来。

通过新的 AdamW，作者证明了 AdamW（重启 AdamWR）在速度和性能方面都与 SGDWR 相当。

这部分看到有点懵逼，不太了解。

---

6. Pytorch的余弦退火学习率策略

详细见参考资料4.

这里补充个额外的插曲，在pytorch其实也实现了余弦退火策略，主要是两个函数：CosineAnnealingLR 与 CosineAnnealingWarmRestarts

• CosineAnnealingLR

这个比较简单，只对其中的最关键的Tmax参数作一个说明,这个可以理解为余弦函数的半周期.如果max_epoch=50次，那么设置T_max=5则会让学习率余弦周期性变化5次.

max_opoch=50, T_max=5

 

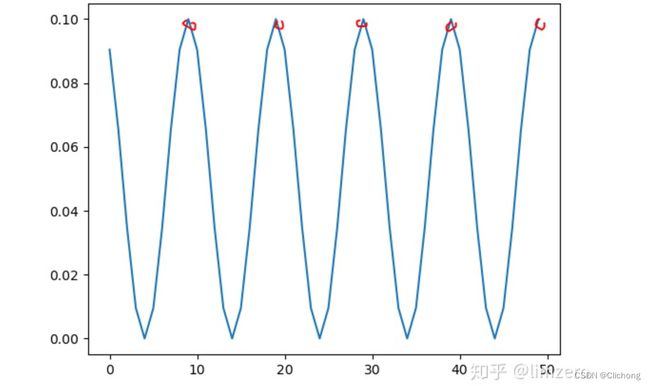
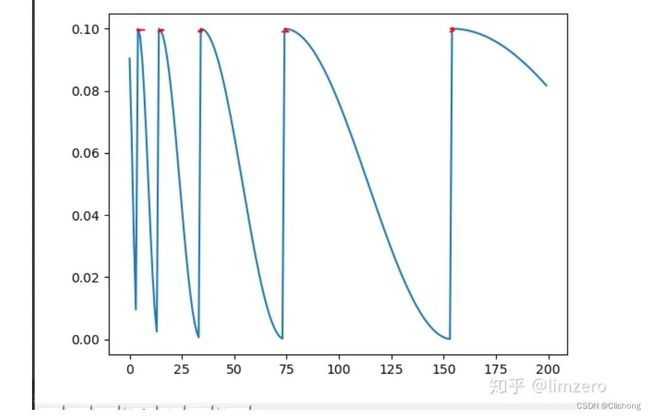
• CosineAnnealingWarmRestarts

这个最主要的参数有两个：T_0是学习率第一次回到初始值的epoch位置；T_mult是控制了学习率变化的速度。

如果$T_{mult}=1$,则学习率在$T_0$，$2\ast T_0$，$3\ast T_0$，$...$，$i\ast T_0$,…处回到最大值(初始学习率)；

T_0=5, T_mult=1

 

如果$T_{mult}>1$，则学习率在$T_0$，$(1+T_{mult})T_0$，$(1+T_{mult}+T_{mult}^2)T_0$，$...$，$(T_{mult}+T_{mult}^2+...+T_{mult}^i)\ast T0$,处回到最大值。

T_0=5, T_mult=2

 

---

参考资料：

1. 模型优化器专栏

2. 自 Adam 出现以来，深度学习优化器发生了什么变化？

3. The 1cycle policy

4. pytorch的余弦退火学习率