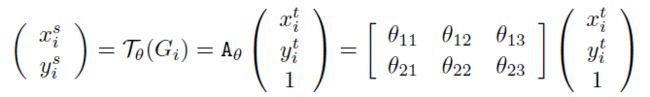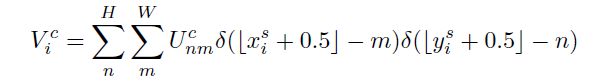论文阅读: Spatial transformer networks
文章目录
-
-
- CNN存在的问题
- Spatial Transformer
- 方法
-
- Localisation Network
- Parameterised Sampling Grid
- Differentiable Image Sampling
- 图片解释
- 例程
- 附录
-
-
- 几种常用的线性变换
- 双线性插值
-
-
CNN存在的问题
CNN定义了非常强大的分类模型,但是仍然受到缺乏在计算和参数效率上对输入数据空间不变性能力的限制。即,当输入图像因随机平移、缩放、旋转、混乱而失真时,CNN模型的分类准确率将会下降。
Spatial Transformer
它是对CNN的改进, 增加了一个Spatial Transformer 模块, 可以对网络内的数据进行空间操作(spatial manipulation). 这个模块可以插入到现有的CNN模块中, 使得网络能够主动的空间变换feature maps, 通过训练确定特定输入对应的空间变换
使用空间变换器的结果是模型能够学习到了对平移、缩放、旋转和更多通用的warping的不变性,得到最先进的性能.
它在这几个方面可以受益:
- 图像分类
- co-localisation(共同定位?), 给定一个包含相同但未知的类的不同实例的图像, 它可以被用于localise, … 不太理解这个地方2333
- spatial attention: spatial transformer可以用于需要注意力机制的任务
方法
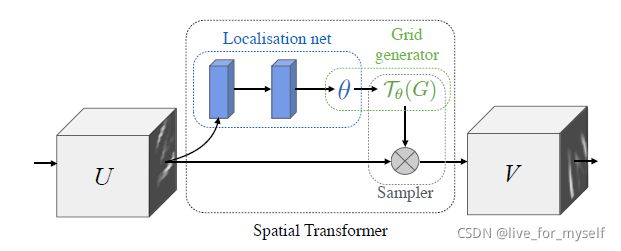
The spatial transformer被分成3个部分, 第一个是localisation network, 它把feature map作为输入, 通过一系列隐层, 输出一些应该被用于spatial transformation的参数,
在第二部分 grid generator中, 这些被预测的参数被用于创造sampling grid, 这是一组点, 输入的map应该被这些点采样成transformed output
最后feature map和 sampling grid 作为sampler的输入, 产生在grid points从输入采样的输出map
总结来说:
它完成的是一个将输入特征图进行一定的变换的过程,而具体如何变换,是通过在训练过程中学习来的,更通俗地将,该模块在训练阶段学习如何对输入数据进行变换更有益于模型的分类,然后在测试阶段应用已经训练好的网络对输入数据进行执行相应的变换,从而提高模型的识别率。
Localisation Network
U ∈ R H ∗ W ∗ C U\text∈ R^{H*W*C} U∈RH∗W∗C: 输入特征图
θ \theta θ: 被用在feature map上的 transformation T θ T_{\theta} Tθ 的参数, θ = f l o c ( U ) \theta \text= f_{loc}(U) θ=floc(U), t h e t a theta theta的大小依赖于transformation的类型, 比如对于二维仿射变换是6维度
对于仿射变换的相关知识参照附录
localisation network function f l o c ( ) f_{loc}() floc() 可以是任何形式, fc 或者CNN都行, 但是最后应该有个regression layer来产生 θ \theta θ
Parameterised Sampling Grid
该层利用Localisation 层输出的变换参数 θ \theta θ,将输入的特征图进行变换
例如输出特征图上某一位置 ( x i t , y i t ) (x^t_i, y^t_i) (xit,yit)根据变换参数 θ θ θ映射到输入特征图上某一位置 ( x i s , y i s ) (x^s_i,y^s_i) (xis,yis),具体如下:
这里使用高度和宽度的归一化坐标
![]()
![]()
Differentiable Image Sampling
为了对输入feature map进行变换, 采样器需使用采样点 T θ ( G ) T_{\theta}(G) Tθ(G) 的集合与输入特征图U一起来生成采样的输出特征图, 输出公式如下:
Φ x , Φ y \Phi_x, \Phi_y Φx,Φy 是一个通用的采样内核k()的参数,它定义了图像的插值(例如,双线性, 整数)。
U n m C U_{nm}^C UnmCis the value at location (n;m) in channel c of the input
V i c V_i^c Vic is the output value for pixel i at location ( x i t ; y i t ) (x^t_i; y^t_i ) (xit;yit) in channel c
请注意,每个输入通道的采样是相同的,因此每个通道都以相同的方式进行转换(这保留了通道之间的空间一致性)
文章指出, 任何可以定义梯度的采样器都可以使用,比如:
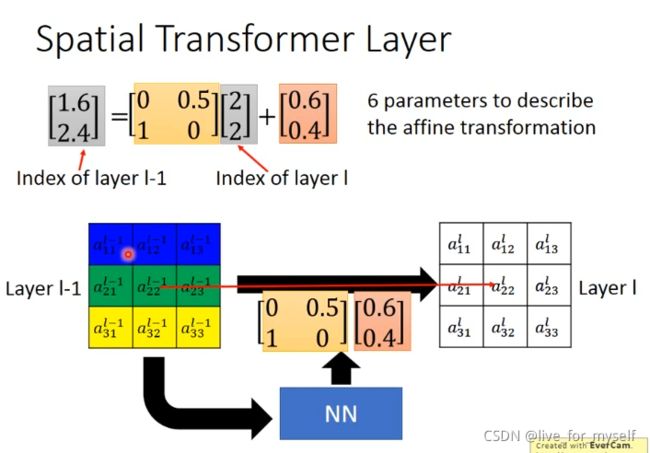
图片解释
例程
在pytorch框架中, F.affine_grid 与 F.grid_sample(torch.nn.functional as F)联合使用来对图像进行变形。
F.affine_grid 根据形变参数产生sampling grid,F.grid_sample根据sampling grid对图像进行变形。
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv2_drop = nn.Dropout2d()
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
# Spatial transformer localization-network
self.localization = nn.Sequential(
nn.Conv2d(1, 8, kernel_size=7),
nn.MaxPool2d(2, stride=2),
nn.ReLU(True),
nn.Conv2d(8, 10, kernel_size=5),
nn.MaxPool2d(2, stride=2),
nn.ReLU(True)
)
# Regressor for the 3 * 2 affine matrix
self.fc_loc = nn.Sequential(
nn.Linear(10 * 3 * 3, 32),
nn.ReLU(True),
nn.Linear(32, 3 * 2)
)
# Initialize the weights/bias with identity transformation
self.fc_loc[2].weight.data.zero_()
self.fc_loc[2].bias.data.copy_(torch.tensor([1, 0, 0, 0, 1, 0], dtype=torch.float))
# Spatial transformer network forward function
def stn(self, x):
xs = self.localization(x)
xs = xs.view(-1, 10 * 3 * 3)
theta = self.fc_loc(xs)
theta = theta.view(-1, 2, 3)
grid = F.affine_grid(theta, x.size())
x = F.grid_sample(x, grid)
return x
def forward(self, x):
# transform the input
x = self.stn(x)
# Perform the usual forward pass
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
x = x.view(-1, 320)
x = F.relu(self.fc1(x))
x = F.dropout(x, training=self.training)
x = self.fc2(x)
return F.log_softmax(x, dim=1)
model = Net().to(device)
附录
此处参见仿射变换
几种常用的线性变换
- 这里可以倒着理解, 比如从B点逆时针旋转, 就好算很多
双线性插值
在对图像进行仿射变换时,会出现一个问题,当原图像中某一点的坐标映射到变换后图像时,坐标可能会出现小数(如下图所示),而我们知道,图像上某一像素点的位置坐标只能是整数,那该怎么办?这时候双线性插值就起作用了。

双线性插值的基本思想是通过某一点周围四个点的灰度值来估计出该点的灰度值

在实现时我们通常将变换后图像上所有的位置映射到原图像计算(这样做比正向计算方便得多),即依次遍历变换后图像上所有的像素点,根据仿射变换矩阵计算出映射到原图像上的坐标(可能出现小数),然后用双线性插值,根据该点周围4个位置的值加权平均得到该点值。过程可用如下公式表示:

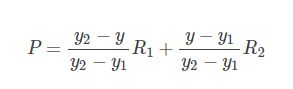
把R1, R2代入, 得:
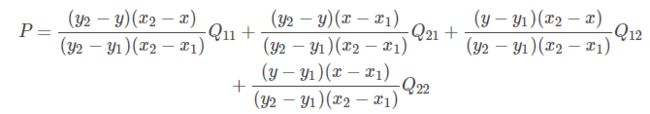
因为 Q 11 , Q 12 , Q 21 , Q 22 Q_{11},Q_{12},Q_{21},Q_{22} Q11,Q12,Q21,Q22 是相邻的四个点,所以 y 2 − y 1 = 1 , x 2 − x 1 = 1 y_2−y_1=1, x_2−x_1=1 y2−y1=1,x2−x1=1,则上式可化简为: