PAC—主成分分析方法

一.PAC方法引入与介绍

 （1）PAC 引入

   如图1所示：

图1.PAC 方法简介

 （2）PAC 基本思想

   如图2所示：

图2.PAC 方法基本思想

 （3）PAC 求解步骤

   【1】原始数据标准化处理
   【2】计算样本 相关系数矩阵
   【3】计算 相关系数矩阵 R的特征值和相应的特征向量
   【4】选择主成分
   【5】计算主成分得分
   【6】依据主成分得分对问题分析与建模

图3.PAC 方法详细步骤

 （4）PAC 方法的作用与利弊

   如图4所示：

图4.PAC 方法的优与劣

二.PAC方法求解实例

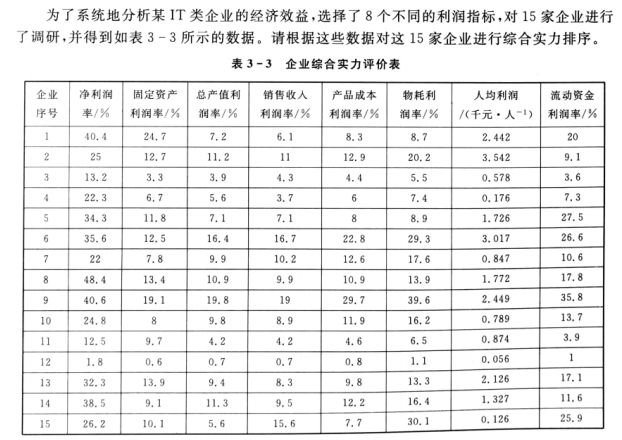
 （1）案例问题

   如图5所示：

图5.问题背景与数据

 （2）求解代码

   如下所示：

%== PCA stepping demonstration program==%

% Read data from a file (e.g. excel) and place it in a matrix.
A=xlsread('Coporation_evaluation.xlsx', 'B2:I16');

% Transfer orginal data to standard data
a=size(A,1);   % Get the row number of A
b=size(A,2);   % Get the column number of A
for i=1:b
    SA(:,i)=(A(:,i)-mean(A(:,i)))/std(A(:,i));  % Matrix normalization
end

% Calculate correlation matrix of A.
CM=corrcoef(SA);

% Calculate eigenvectors and eigenvalues of correlation matrix.
[V, D]=eig(CM);

% Get the eigenvalue sequence according to descending and the corrosponding
% attribution rates and accumulation rates.
for j=1:b
    DS(j,1)=D(b+1-j, b+1-j);
end
for i=1:b
    DS(i,2)=DS(i,1)/sum(DS(:,1));
    DS(i,3)=sum(DS(1:i,1))/sum(DS(:,1));
end         

% Calculate the numvber of principal components.
T=0.9;  % set the threshold value for evaluating information preservation level.
for K=1:b
    if DS(K,3)>=T
        Com_num=K;
        break;
    end
end

% Get the eigenvectors of the Com_num principal components
for j=1:Com_num
    PV(:,j)=V(:,b+1-j);
end

% Calculate the new socres of the orginal items
new_score=SA*PV;

for i=1:a
    total_score(i,2)=sum(new_score(i,:));
    total_score(i,1)=i;
end
new_score_s=sortrows(total_score,-2);

% Displays result reports
disp('特征值及贡献率：')
DS
disp('阀值T对应的主成分数与特征向量：')
Com_num
PV
disp('主成分分数：')
new_score
disp('主成分分数排序：')
new_score_s

三.PAC方法总结

 （1）详细讲述步骤：

     【1】由于原始数据的数量级（量纲）常常不同，所以我们首先要对不同的变量类型进行标准化，消除量纲的影响。具体就是每个值减去该变量类型均值然后除以该变量类型的标准差。
     【2】计算样本相关系数矩阵就直接是按照图6方式求解即可，图3中公式有误。

图6.求协方差

     【3】计算相关系数矩阵R的特征值和相应的特征向量。使用函数可直接求得[V,D]。矩阵V是一列列的特征向量，而D是对角矩阵，对角线上的值就是特征值，并且特征值是由小到大排序的（越往右下）。
     【4】将特征值由大到小排序，然后计算贡献度和累计贡献度：贡献度=特征值/特征值之和；累计贡献度=从第一行到此行特征值之和/总特征值之和。
     【5】设定阈值，选择主成分（特征值和对应的特征向量）。规定阈值T是主成分需要累计的贡献度。当累计贡献度大于等于T即完成特征值的选择。
     【6】翻转得到主成分包含的特征值对应的特征向量。将标准化矩阵映射到主成分上。计算每一组得分：得分=每一行主成分得分之和。就得到了原始数据在主成分（降维）上的得分。

%读取数据
A=xlsread('Coporation_evaluation.xlsx', 'B2:I16');

%获得A的行数和列数
a=size(A,1);   
b=size(A,2);   
for i=1:b
    %A矩阵标准化处理为SA：（每一个值-该列平均值）/该列标准差
    SA(:,i)=(A(:,i)-mean(A(:,i)))/std(A(:,i));  
end

%获得标准化矩阵SA的相关系数矩阵
CM=corrcoef(SA);

%获得相关系数矩阵的特征值D和对应的特征向量V
[V, D]=eig(CM);

%将特征值从大到小排序
for j=1:b
    DS(j,1)=D(b+1-j, b+1-j);
end
for i=1:b
    %计算贡献度（贡献度=特征值/特征值之和）
    DS(i,2)=DS(i,1)/sum(DS(:,1));
    %计算累计贡献度（累计贡献度=从第一行到此行特征值之和/总特征值之和）
    DS(i,3)=sum(DS(1:i,1))/sum(DS(:,1));
end         

%选择主成分（特征值）
T=0.9;  
for K=1:b
    %规定T是主成分需要累计的贡献度
    %当累计贡献度大于等于T即完成特征值的选择（由D(1,1)到D（Com_num,1））
    if DS(K,3)>=T
        Com_num=K;
        break;
    end
end

%因为之前将特征值反转（从函数返回的默认从小到大返回为从大到小），而每个特征值对应的特征向量也应该是“逆对应”关系
%获得主成分特征值对应的特征向量（特征值由1到Com_num,特征向量由到倒数第一到倒数第Com_num）
for j=1:Com_num
    PV(:,j)=V(:,b+1-j);
end

%将标准化矩阵映射到主成分上（降维）获得主成分得分矩阵(标准化消除量纲+主成分映射降维)new_score
new_score=SA*PV;

%计算得分
for i=1:a
    %得分=每一行主成分得分之和
    total_score(i,2)=sum(new_score(i,:));
    %设置序号
    total_score(i,1)=i;
end
%按照第二列进行排序。负整数表示排序顺序为降序。
new_score_s=sortrows(total_score,-2);

disp('特征值及贡献率：')
DS
disp('阀值T对应的主成分数与特征向量：')
Com_num
PV
disp('主成分分数：')
new_score
disp('主成分分数排序：')
new_score_s

 （2）意义分析：

     【1】PCA主成分分析方法：
       针对于：多个变量存在一定相关性时；
       适用于：变量个数较多或者变量之间存在复杂的关系时；
       作用是：消除评价指标间的相关影响（如果互相有关联关系，则都评价肯定是不合理不客观不公正的，关联性越强越不合理PAC作用越强）。可减少指标选择工作量（减少指标个数）。
     【2】案例作用分析：
       企业的各个评价指标之间明显是有关联的。所以直接标准化然后计算得分是不合理的。主成分分析法就提取出互不相关的变量（维度），然后标准化数据进行映射，提取出主成分来评价。作用：（主要）是消除了指标之间的相关影响，（次要）是减少了变量个数减少了计算。

四.函数解释和参考文案

 （1）函数解释：

   【1】std(A)：求向量A的标准差。
   【2】mean(A)：求矩阵A的平均值。
   【3】corrcoef(A)：求矩阵A的相关系数矩阵。
   【4】eig(A)=[V,D]：求矩阵A的全部特征值，构成对角阵D，并求A的特征向量构成V的列向量。
   【5】 sortrows (X, COL)：按指定列COL由小到大进行排序。若COL为负数表示按照降序排列。

 （2）参考文案：

    对角矩阵
   知乎-简洁全面PCA方法讲述