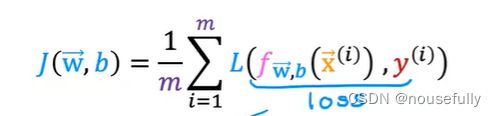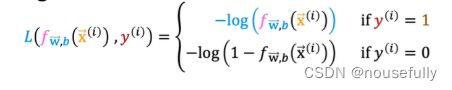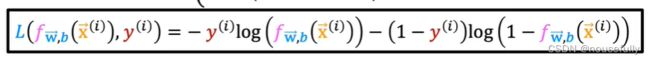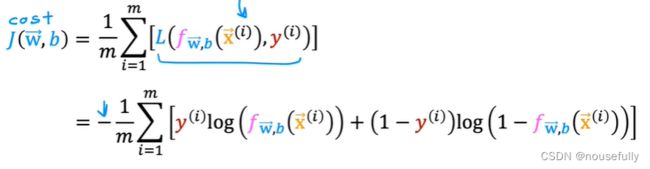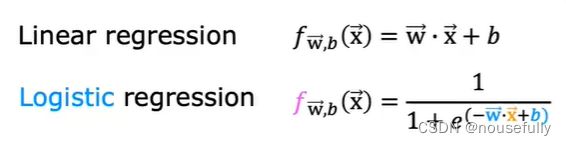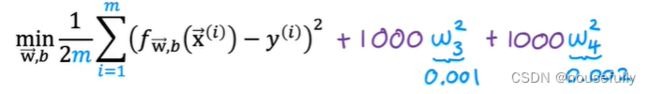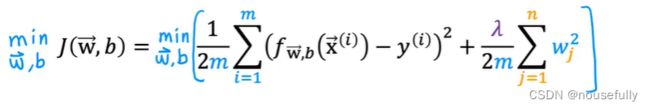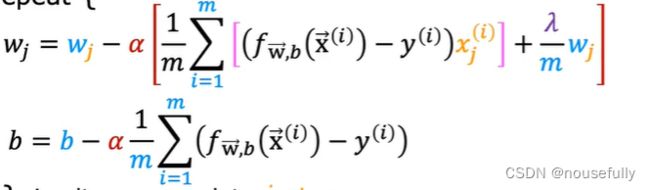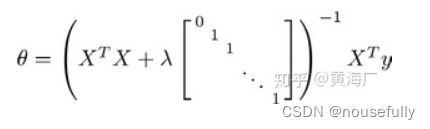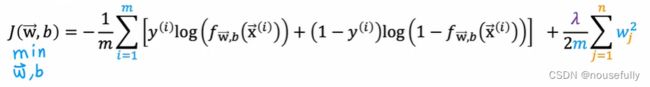2022吴恩达机器学习第三周
6、逻辑回归
6-1、分类问题
在分类问题中，你要预测的变量y是离散的值，我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法，这是目前最流行使用最广泛的一种学习算法。
我们从二元的分类问题开始讨论。
我们将因变量(dependent variable)可能属于的两个类分别称为负向类（negative class）和正向类（positive class），则因变量
，其中 0 表示负向类，1 表示正向类。
6-2、假说表示
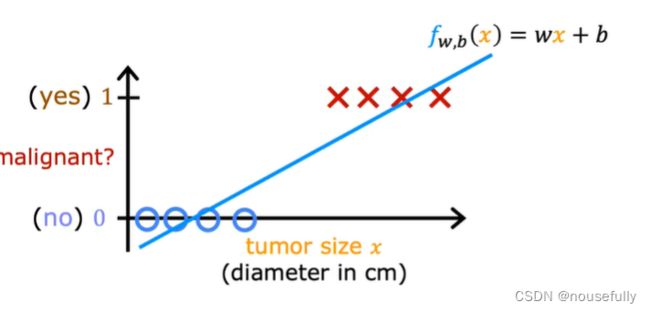
根据线性回归模型我们只能预测连续的值，然而对于分类问题，我们需要输出0或1，我们可以预测：
对于上图所示的数据，这样的一个线性模型似乎能很好地完成分类任务。假使我们又观测到一个非常大尺寸的恶性肿瘤，将其作为实例加入到我们的训练集中来，这将使得我们获得一条新的直线。
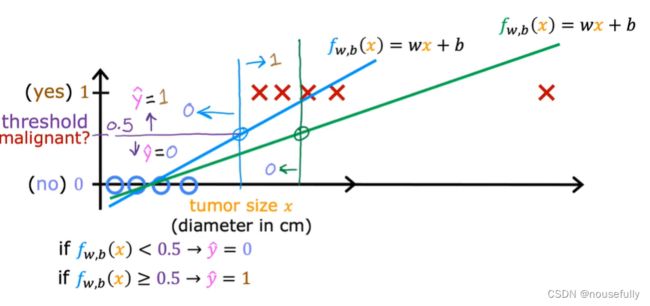
这时，再使用0.5作为阀值来预测肿瘤是良性还是恶性便不合适了。可以看出，线性回归模型，因为其预测的值可以超越[0,1]的范围，并不适合解决这样的问题。
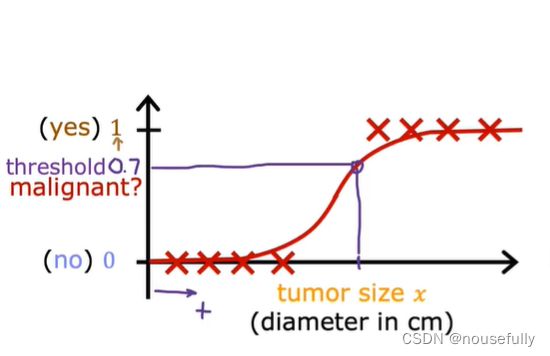
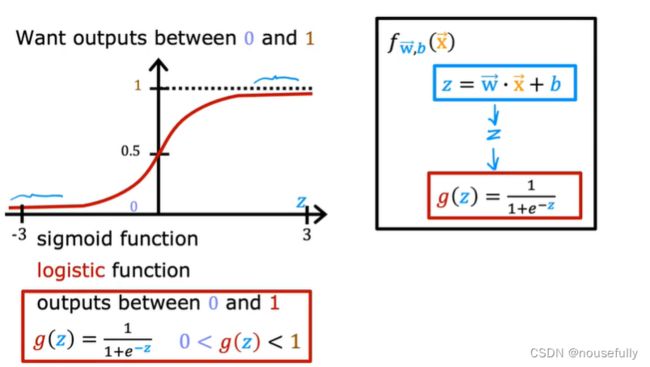
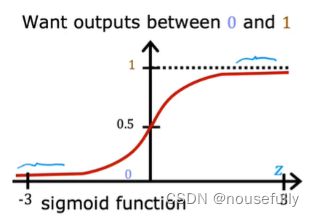
我们引入一个新的模型，逻辑回归，该模型的输出变量范围始终在0和1之间。 逻辑回归模型的假设是：
x 代表特征向量
g 代表逻辑函数（logistic function)是一个常用的逻辑函数为S形函数（Sigmoid function），
f(x)的作用是，对于给定的输入变量，根据选择的参数计算输出变量=1的可能性（estimated probablity）
例如，如果对于给定的 X ，通过已经确定的参数计算得出 f（x）=0.7 ，则表示有70%的几率 为正向类，相应地为负向类的几率为1-0.7=0.3。
6-3、判断边界
决策边界(decision boundary)这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。
在逻辑回归中，我们预测：
当 f(x)>=0.5 时，预测y=1 。
当 f(x)<0.5 时，预测y=0 。
根据上面绘制出的 S 形函数图像，我们知道当
z=0 时g(z)=0.5
z>0 时g(z)>0.5
z<0时 g(z)<0.5
又z=
，即：
>=0 时，预测 y=1
<0 时，预测 y=0
也就是z>=0,g(z)>0.5,f(x)>0.5,y=1.
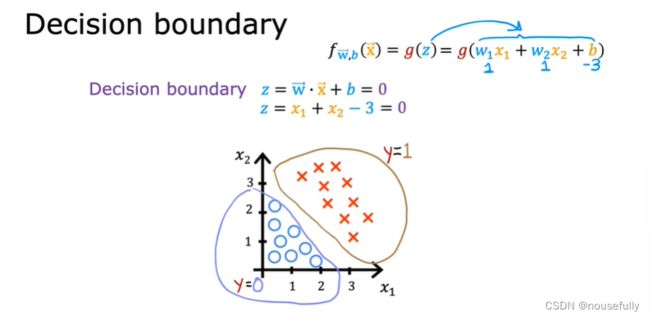
现在假设我们有一个模型：
并且参数w是向量[-3 1 1]。 则当-3+x1+x2>=0，即x1+x2>=3 时，模型将预测y=1。
即可绘制x1+x2=3，这条线既是我们模型的分界线，即预测为1和预测为0的区域分隔开。
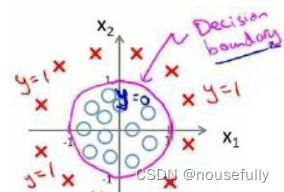
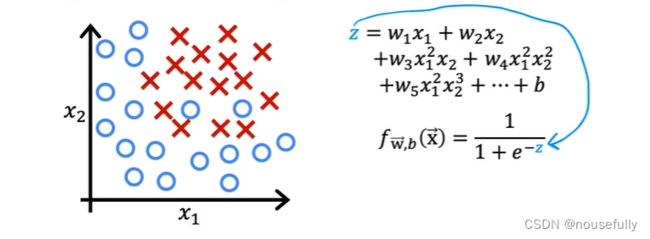
假使我们的数据呈现这样的分布情况，怎样的模型才能适合呢？
因为需要用曲线才能分隔 0 的区域和 1 的区域，我们需要二次方特征：
假设：
) 是[-1 0 0 1 1]，z=-1+
+
，
令z>0，+>1，则我们得到的判定边界恰好是圆点在原点且半径为1的圆形。
我们可以用非常复杂的模型来适应非常复杂形状的判定边界。
6-4、代价函数
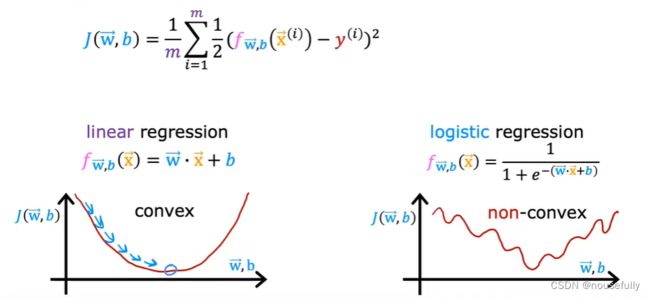
对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将 f(x) 带入到这样定义了的代价函数中时，我们得到的代价函数将是一个非凸函数（non-convexfunction）。
这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值。
我们重新定义逻辑回归的代价函数为：
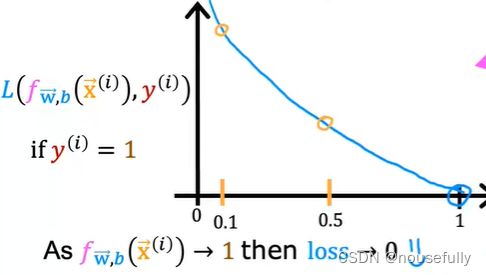
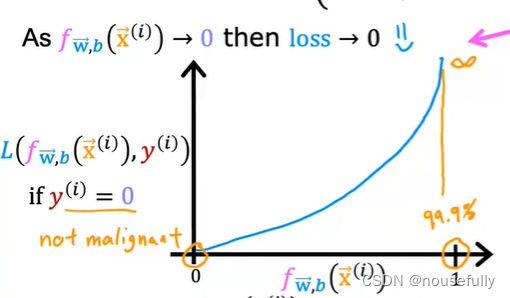
f(x) 和 L(f(x),y) 之间的关系如下图所示：
这样构建的 L(f(x),y) 函数的特点是：当实际的 y=1 且 f(x) 也为 1 时误差为 0，当 y=1 但 f(x) 不为1时误差随着变小而变大；当实际的 y=0 且 f(x) 也为 0 时代价为 0，当 y=0 但 f(x) 不为 0时误差随着 f(x) 的变大而变大。
构建的代价函数简化为：交叉熵
代入代价函数为：
python代码实现：
import numpy as np
def cost(theta, X, y):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
return np.sum(first - second) / (len(X))当使用梯度下降法来实现逻辑回归时，我们有这些不同的参数 w ，就是 w1,w2,w3 一直到 wn ，我们需要用这个表达式来更新这些参数。我们还可以使用 for循环来更新这些参数值，用 for i=1 to n，或者 for i=1 to n+1。当然，不用 for循环也是可以的，理想情况下，我们更提倡使用向量化的实现，可以把所有这些 n 个参数同时更新。
这个特征缩放的方法，也适用于逻辑回归。如果你的特征范围差距很大的话，那么应用特征缩放的方法，同样也可以让逻辑回归中，梯度下降收敛更快。
7、正则化
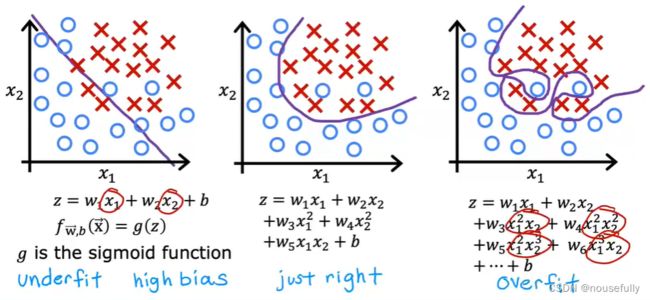
7-1、过拟合问题
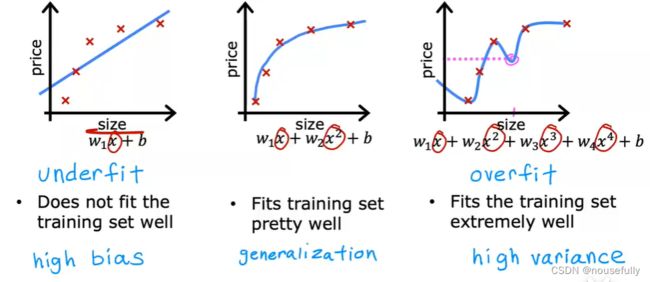
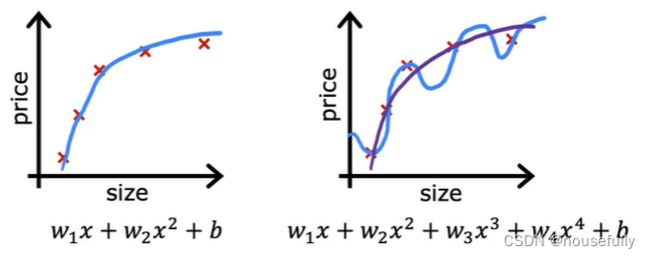
如果我们有非常多的特征，我们通过学习得到的假设可能能够非常好地适应训练集（代价函数可能几乎为0），但是可能会不能推广到新的数据。
第一个模型是一个线性模型，欠拟合，不能很好地适应我们的训练集；第三个模型是一个四次方的模型，过于强调拟合原始数据，而丢失了算法的本质：预测新数据。
我们可以看出，若给出一个新的值使之预测，它将表现的很差，是过拟合，虽然能非常好地适应我们的训练集但在新输入变量进行预测时可能会效果不好；
分类中也存在这样的问题：
就以多项式理解， 的次数越高，拟合的越好，但相应的预测的能力就可能变差。
处理过拟合：
1、收集更多的数据
2、丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征。使用自动选择最合适的特征用于预测任务的算法（例如PCA）
3、正则化，保留所有的特征，但是减少参数的大小（magnitude）
7-2、正则化代价函数
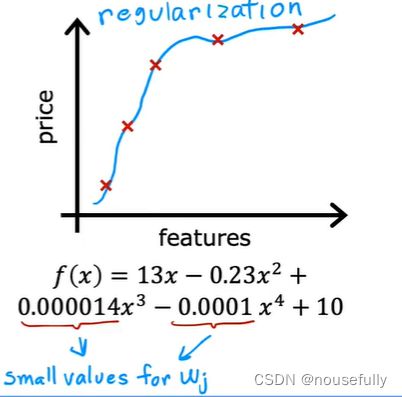
我们可以从之前的事例中看出，正是那些高次项导致了过拟合的产生，所以如果我们能让这些高次项的系数接近于0的话，我们就能很好的拟合了。
所以我们要做的就是在一定程度上减小这些参数w的值，这就是正则化的基本方法。我们决定要减少w3和w4的大小，我们要做的便是修改代价函数，在其中w3 和w4 设置一点惩罚。这样做的话，我们在尝试最小化代价时也需要将这个惩罚纳入考虑中，并最终导致选择较小一些的 w3和w4。
通过这样的代价函数选择出的w3 和 w4对预测结果的影响就比之前要小许多。假如我们有非常多的特征，我们并不知道其中哪些特征我们要惩罚，我们将对所有的特征进行惩罚，并且让代价函数最优化的软件来选择这些惩罚的程度。
这样的结果是得到了一个较为简单的能防止过拟合问题的假设：
其中
又称为正则化参数（Regularization Parameter）。
注：根据惯例，我们不对b进行惩罚。
如果我们令 的值很大的话，为了使Cost Function 尽可能的小，所有的 w 的值（不包括）都会在一定程度上减小。
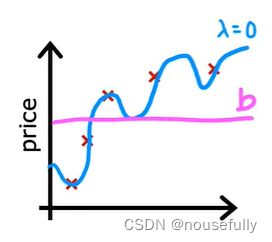
如果选择的正则化参数 过大，则会把所有的参数都最小化了，导致模型变成b ，也就是上图中红色直线所示的情况，这样我们所得到的只能是一条平行于 x 轴的直线。造成欠拟合。
所以对于正则化，我们要取一个合理的 的值，这样才能更好的应用正则化。
回顾一下代价函数，为了使用正则化，让我们把这些概念应用到到线性回归和逻辑回归中去，那么我们就可以让他们避免过度拟合了。
7-3、正则化线性回归
对于线性回归的求解，我们之前推导了两种学习算法：一种基于梯度下降，一种基于正规方程。
正则化线性回归的代价函数为：
如果我们要使用梯度下降法令这个代价函数最小化，因为我们未对 b 进行正则化，所以梯度下降算法将分两种情形：
可以看出，正则化线性回归的梯度下降算法的变化在于，每次都在原有算法更新规则的基础上令 w 值减少了一个额外的值。
我们同样也可以利用正规方程来求解正则化线性回归模型，方法如下所示：
图中的矩阵尺寸为 (n+1) * (n+1) 。
7-4、 正则化的逻辑回归模型
针对逻辑回归问题，我们在之前的课程已经学习过两种优化算法：我们首先学习了使用梯度下降法来优化代价函数 J(w,b) ，接下来学习了更高级的优化算法，这些高级优化算法需要你自己设计代价函数 J(w,b)
Python代码：
import numpy as np
def costReg(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X*theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X*theta.T)))
reg = (learningRate / (2 * len(X))* np.sum(np.power(theta[:,1:theta.shape[1]],2))
return np.sum(first - second) / (len(X)) + reg如果我们要使用梯度下降法令这个代价函数最小化，因为我们未对 b 进行正则化，所以梯度下降算法将分两种情形：
注：看上去同线性回归一样，但是知道 f(x)=g(x) ，所以与线性回归不同。
注意：
- 虽然正则化的逻辑回归中的梯度下降和正则化的线性回归中的表达式看起来一样，但由于两者的 f(x) 不同，所以还是有很大差别。
- b不参与其中的任何一个正则化。