机器学习(深度学习)中的反向传播算法与梯度下降

这是自己在CSDN的第一篇博客，目的是为了给自己学习过的知识做一个总结，方便后续温习，避免每次都重复搜索相关文章。

一、反向传播算法

定义：反向传播(Backpropagation，缩写为BP)是“误差反向传播”的简称，其与最优化方法(如梯度下降法)的结合使用 是 用来训练人工神经网络的常用方法。
(该部分的讲解主要参考aift博主的原创文章：“反向传播算法”过程及公式推导（超直观好懂的Backpropagation）)

上图为一个前向(前馈)运算，激活函数为sigmoid:(1/(1+np.exp(-x)))，其导数为:sigmoid(1-sigmoid)
其中：
①i1，i2下方的0.05与0.10表示输入神经元 输出 给后面层的初始值
②o1与02下方的0.01与0.99表示输出神经元的目标输出(target)
③w 12345678 左侧的是其初始权重值
④偏置b1 2的值为0.35与0.60，图示于最下方。

附：
{
①偏置的作用：增加神经元拟合的灵活性。

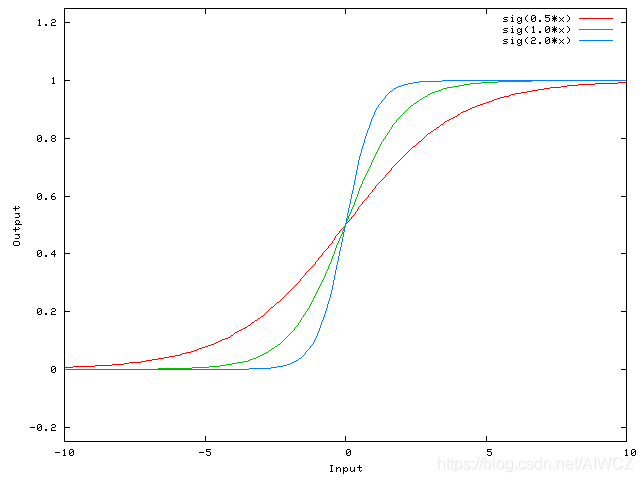
不同的w，输出曲线都相交于一点(0,0.5)。输出曲线只能改变形状，不能挪动位置，网络分类的表现力大大受限。
增加偏置后：
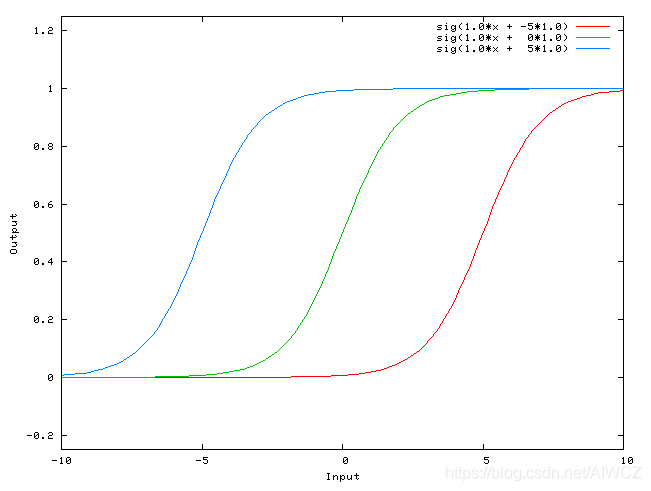②采用Batch Normalization后还需要偏置吗？
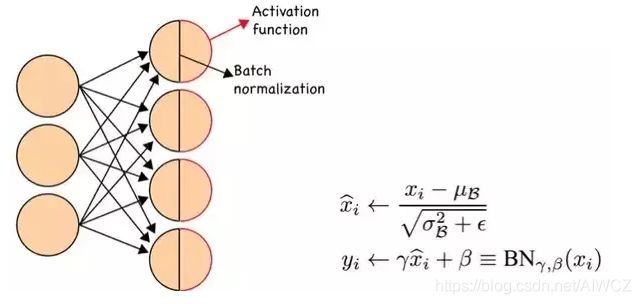由于经过BN层后，会减去均值μB，因此对于所有xi而言，增加的偏置参数b都会被减去，所以此时偏置b是不需要的。
从：

到：

但并不是不需要偏置了，BN层用β参数作为了新的偏置项。

除了BN以外，还有其他归一化方法，例如LN，IN，GN，这篇文章是个不错的参考：BN，LN，IN，GN都是什么？不同归一化方法的比较

BN的成功多数人认为与内部协方差(ICS)偏移有关，但MIT的这项研究NIPS 2018 | MIT新研究参透批归一化原理 认为两者并无关系，对该领域感兴趣可以进一步研究。
}

下面是反向传播(求网络误差对各个权重参数(即w 12345678)的梯度)：
我们先来求最简单的，求误差E对w5的导数。首先明确这就是一个“链式求导”过程，求出导数，也就是梯度，具体请仔细理解下图。
此时，总误差对w5的梯度已经计算出来，利用梯度下降原理，进行参数更新，如下图：
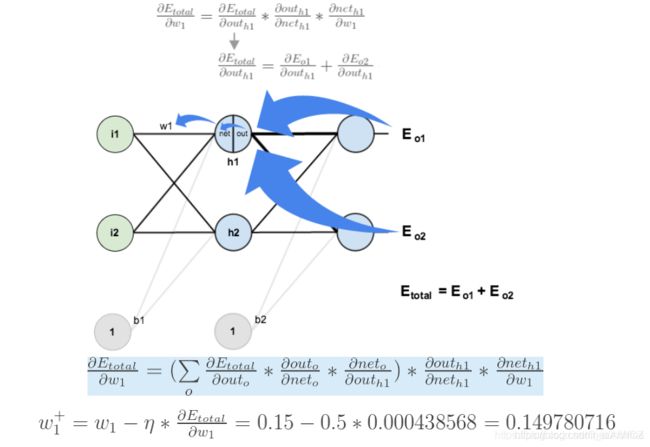
如果要想求误差E对w1的梯度，误差E对w1的求导路径不止一条，这会稍微复杂一点，但换汤不换药，计算过程如下所示：

二、梯度下降

目的：给定 目标函数|损失函数|代价函数|误差函数 ，根据梯度寻找函数值最小时，最优 自变量|参数 的值。
可能出现的问题：
由于深度神经网络1.较深的深度 2.非线性函数 这两个主要因素，导致目标的损失函数很容易为非凸函数，损失函数曲面中包含许多驻点，而驻点又分为：1.鞍点 2.局部极小值 3.全局极小值(希望能够找到的)

①对于非凸函数的梯度下降优化，容易陷入1.局部极小值2.鞍点。

②过拟合。

{附定义：
1.驻点：函数的一阶导数为0的点(驻点也称为稳定点，临界点)。对于多元函数，驻点是所有一阶偏导数都为零的点。

2.拐点：设函数y=f(x)在点x0的某邻域内连续，若（x0，f（x0））是曲线y=f(x)凹与凸的分界点，则称（x0，f（x0））为曲线y=f(x)的拐点。
如何判定拐点：1，若函数二阶可导，某点二阶导数值为零，两端二阶导数值异号。2，若函数三阶可导，则二阶导数为0，三阶导数不为0的点就是拐点。
注：拐点（x0，f（x0））是曲线上的一点，它有横坐标和纵坐标，不要只把横坐标当成拐点。

3.鞍点：
不准确定义：从正交的两个方面来看中间那个点，在一个方向上它是极大值，在另一个方向上它是极小值。

鞍点对Gradient Descent的影响较大，在许多深度学习实验中，往往会有存在鞍点的可能，而若是鞍点较多，则会严重影响Gradient Descent的性能与正确率，而事实上即便在其他算法中，鞍点往往比Local optima更令人头疼，而关于如何解决、或者说避开鞍点，可以参考[How to Escape Saddle Points Efficiently]

4.一些联系：
①对于可导函数，极值点必定是驻点。
②拐点不一定是驻点，驻点也不一定是拐点。
}

三、梯度下降常见算法

介绍批量梯度下降、随机梯度下降、批次梯度下降三种方法，其区别仅限于：采用多少数据来计算目标函数的梯度来更新参数。即对参数更新的准确性与梯度计算时间采用不同的偏向。

①Batch Gradient Descent(也是标准梯度下降)
更新规则：采用整个训练集的数据来计算 目标函数|损失函数|代价函数|误差函数 对参数的梯度。

下式为批量梯度下降一般形式。(其中η表示学习率，后者表示梯度向量)

优点：对于凸函数可以确保收敛到全局极小值，对于非凸函数可以确保收敛到某个局部极小值。
缺点：每一次更新需要对整个数据集计算梯度，耗时大。

②Stochastic Gradient Descent
**更新规则：**对每个样本计算梯度后，就会对参数进行更新

优点：
①参数更新速度快(训练速度快)。
②对于非凸函数，较批量随机梯度下降而言，有机会优化至更好的局部极小值。
缺点：
①并不是每次的参数更新都是朝着整体最优的方向，目标函数|损失函数|代价函数|误差函数 震荡较大，对于凸函数的优化而言，较难优化至全局最优点。

与BGD的联系：无限减少学习率η后，SGD与BGD的收敛结果无限逼近。

③Mini-Batch Gradient Descent
更新规则：是上述两种方法更新规则的折中，每次既不使用全部数据也不使用单个数据，而是使用预设定Batch_Size的数据，进行梯度计算，并更新参数。
下图为三种梯度下降方法收敛过程示意图。

优点：
①利用并行化运算，在一个batch的数据上优化网络参数，不会比单个数据慢太多。
②大大减少收敛所需的迭代次数，同时可以使其更接近全局最优的优化方向。
缺点
①Batch_Size需要合理取值，增加一定调参难度。

总结：至此已简要阐述了一阶优化器BGD、SGD、MBGD，但他们都存在如下三个问题。
①位于局部最小值或鞍点时有可能停止优化。
②希望对出现频率低的特征进行较大的更新。

针对以上出现的问题①，出现了移动指数加权平均与动量的概念，来解决上述问题，并提出了下述的两类优化器。

④Momentum xGD(指动量与上述某种梯度下降方式的结合)
提出的目的缓解网络损失函数训练时，小学习率时收敛速度过慢，大学习率时震荡过大的情况。
缓解的方法：将动量的概念引入到参数更新中。在这里，我们可以简单的把动量理解为惯性。
那么在每次进行参数更新前，会参考(这个参考就是惯性的体现)之前数据计算出的梯度(就是下图公式12中的前半部分)，再结合本次计算的梯度(下图公式12的后半部分)，两者相加最终得出本次参数更新采用的梯度(即Vdw与Vdb)。

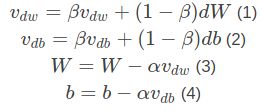
实现的方法：上面动量引入的实现就是基于梯度的移动指数加权平均。
①从而具有吸收瞬时突发的能力，也就是平稳性(使得得到的曲线趋势能够更加平缓)，减少损失函数的震荡。
②经过迭代可以得出，越靠前的梯度向量，会受到β这个系数(默认取0.9，取值越大收敛越稳定，但也越不容易跳出局部最小值)的指数式衰减，因此会让其有机会跳出局部最优点，摆脱前面数据的束缚。
{
附：
可以采用数据的直接平均吗？
不可以。
主要原因是：当训练到后期，每次对海量已遍历数据进行平均，计算量将非常大，因此采用移动平均进行近似。

移动指数加权平均的偏差修正
当我们将衰减系数β取得非常大的时候，曲线拟合的初期和我们的真实值差距将非常大，如下图中紫色的线。
这个时候采用带修正偏差的指数加权平均公式进行：
(1-βt)是修正的系数，当解决了初期的差距后，训练到后期，t足够大时，Vt’ = Vt。

}

⑤Nesterov Accelerated Gradient(NAG)
与动量法的区别直白来说，就是反正要往前走一步，不如先走这一步，再看路。
这个往前走一步就是历史梯度产生的动量。
下面两个图分别是momentum下降法示意图与NAG下降法示意图。来自深度学习优化函数详解（5）-- Nesterov accelerated gradient (NAG)
两者唯一的区别就是，momentum下降法在B点计算当前梯度，NAG下降法在超前点C处计算当前梯度。

但在优化的过程中，某些变量可能很快得就优化到了极小值附近，而有些可能还在梯度很大的地方，这个时候采用全局统一的学习率就会使前者不稳定后者收敛慢，另外对于经常更新的参数，我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些；对于偶尔更新的参数，我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些。
即根据参数的重要性而对不同的参数进行不同程度的更新。

⑥Adagrad （Adaptive gradient）
梯度更新规则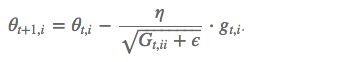：我们的出发点是：即根据参数的重要性而对不同的参数进行不同程度的更新。，而在Adagrad中就是用Gt,ii，来量化这个重要性或更新频率。
Gt,ii 是一个二阶动量，表示该参数，迄今为止所有梯度值的平方和。

在机器学习的应用中，AdaGrad非常适合样本稀疏的问题，因为稀疏的样本下，每次梯度下降的方向，以及涉及的变量都可能有很大的差异。
AdaGrad的缺点是虽然不同变量有了各自的学习率，但是初始的全局学习率还是需要手工指定。如果全局学习率过大，优化同样不稳定；而如果全局学习率过小，因为AdaGrad的特性，随着优化的进行(Gt,ii累计的梯度过多)，学习率会越来越小，很可能还没有到极值就停滞不前了。

⑦Adadelta⑧Root Mean Square Prop(RMSProp)

由于AdaGrad单调递减的学习率变化过于激进，我们考虑一个改变二阶动量计算方法的策略：不累积全部历史梯度，而只关注过去一段时间窗口的下降梯度。这也就是AdaDelta名称中Delta的来历。
修改的思路很简单。前面我们讲到，指数移动平均值大约就是过去一段时间的平均值，因此我们用这一方法来计算二阶累积动量：
这就避免了二阶动量持续累积、导致训练过程提前结束的问题了。（RMSProp方法基本相同）

⑨Adam：Adaptive Moment Estimation
Adam = Adaptive + Momentum
将一阶动量和二阶动量结合起来。

⑩Nadam(集大成者)
Nadam = Nesterov + Adam

References

[1]https://www.cnblogs.com/guoyaohua/p/8542554.html
[2]https://blog.csdn.net/malefactor/article/details/78768210?utm_source=blogxgwz5#commentBox
[3]https://blog.csdn.net/qq_32623363/article/details/96334862
[4]https://blog.csdn.net/ft_sunshine/article/details/90221691#commentBox
[5]https://blog.csdn.net/willduan1/article/details/78070086
[6]https://blog.csdn.net/tsyccnh/article/details/76673073
[7]https://zhuanlan.zhihu.com/p/32230623