SMOTE算法原理 易用手搓小白版 数据集扩充 python

前言

为啥要写这个呢，在做课题的时候想着扩充一下数据集，尝试过这个过采样降采样，交叉采样，我还研究了一周的对抗生成网络，对抗生成网络暂时还解决不了我要生成的信号模式崩塌的问题，然后就看着尝试一下别的，就又来实验了一下SMOTE，我看原理也不是很难，想着调库的话不如自己手搓一个稍微，可以简单理解一点的，最后呢也是成功了，然后呢对训练集进行了扩充，效果额，训练集准确率肯定是嗷嗷提升，训练的效果稳定了一点，但是测试集出来的效果，感觉变化不大，可能是我实验样本比较少的原因，说明普通的SMOTE还是比较吃原始数据分布，我写的这个是只用numpy 和 random 两个库，内容都是手搓的，和官方例程最大的不同，就是官方例程控制的是生成样本和原样本的比例，本程序控制的是生成样本的数量。也就是可以直接指定生成样本的数量进行输出。

---

一、SMOTE理论

SMOTE算法是一种2002年发表的根据样本之间的关系，生成新样本的，扩充数据集的算法，论文源地址贴在下面，然后用一个图表示一下一个样本的生成过程

SMOTE: Synthetic Minority Over-sampling Technique:
论文地址: https://www.jair.org/index.php/jair/article/download/10302/24590

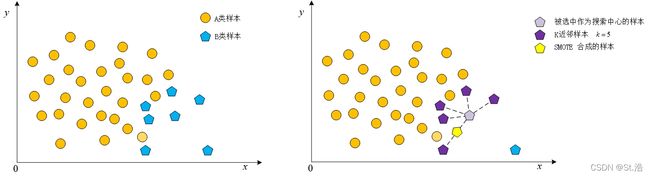
虽然别人的图画的很好，但是想到自己作为一个研究生，还是少复制粘贴，代码都手搓了图也忍痛不复制自己画一下，好了，进入正题
描述一下这个图，可以看到图中分布着两种样本点，因为五边形表示的这一类的样本点为少数类样本，所以个图里选择五边形这一类样本进行扩充，随机认定一个五边形样本点为中心，搜索离它距离最近的K个同类样本点(也就是五边形样本点)，随机选择一个被搜索到的样本点，用最开始认定的作为搜索中心的样本点和后来被随机选中的样本点生成一个新的样本。
那通过两个样本点是如何生成一个新的样本点呢这里用到的就是一个重要的线性代数的知识

对于 $x_1,x_2$如果$\lambda \in [0,1]$则 $\lambda x_1+(1-\lambda )x_2$一定在$x_1和x_2$的连线上

其中$\lambda x_1+(1-\lambda )x_2$也可以转换为$x_2+\lambda (x_1-x_2)$或者$x_1+\lambda (x_2-x_1)$下图中$x_3$为$x_1$和$x_2$连接线上的一点，用初中的移项等知识就一定可以求到一个$\lambda$，好了初中知识就不赘述了

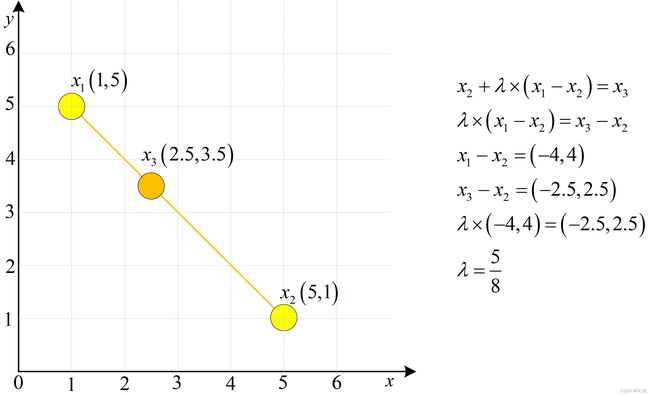
因此可以通过随机生成一个0~1之间的数结合两个样本点就能合成一个新的数据

二.python代码

实际应用中定义一个class 类来实现功能在实例中定义了三个子函数
class SMOTE(object):
初始化函数
def __init__(self,sample,k=2,gen_num=3):
获取相邻点的函数
def get_neighbor_point(self):
获取合成的样本的函数
def get_syn_data(self):
后面依次介绍，首先调用一下需要用到的基础库

import numpy as np     
import random   #用于生成随机数
import matplotlib.pyplot as plt  #画图

2.1初始化部分

初始化部分需要输入三个参数
1.被扩充的样本
2.Smote算法需要设置的K值
3.生成样本的数量

    def __init__(self,sample,k=2,gen_num=3):
        #需要被扩充的样本
        self.sample = sample      
        #获取输入数据的形状
        self.sample_num,self.feature_len = self.sample.shape
        #近邻点  
        self.k = min(k,self.sample_num-1)
        #需要生成的样本的数量                
        self.gen_num = gen_num    
        # 定义一个数组存储生成的样本
        self.syn_data = np.zeros((self.gen_num,self.feature_len))  
		# 定义一个数组存储每一个点和其临近点的坐标
        self.k_neighbor = np.zeros((self.sample_num,self.k),dtype=int)  

先不用思考接下来我对每一句话进行解释

首先是获取数据样本的长和宽

#需要被扩充的样本
self.sample = sample      
#获取输入数据的形状
self.sample_num,self.feature_len = self.sample.shape  

举个例子如果输入的的样本的形状是10✖2的
也就意味着输入了10个样本
每一个样本有2个特征也就是一个样本由2个数构成
对应到代码中样本数量数据被存储到了self.sample_num=10
样本长度数据被存储到了self.feature_len=2
为什么要获取这两个数据呢先从这一句开始解释

self.k = min(k,self.sample_num-1)

如果输入的需要被扩充的数据有10个样本，也就是说每一个样本最多有10-1也就是9个相邻的点（样本），也就是相对输入数据中的每一个样本点，他能搜索到的邻近样本数量是有上限的，因此避免输入K值过大，超过能搜索的最大值，就需要结合输入样本的数量（self.sample_num）进行约束

接下来看最后三句，根据输入的需要生成的样本的数量（self.gen_num），和我们已经知道的每一个样本的长度（self.feature_len）,就能生成一个self.syn_data形状是（self.gen_num×self.feature_len）的全0数组存储生成的数据

#需要生成的样本的数量                
self.gen_num = gen_num    
# 定义一个数组存储生成的样本
self.syn_data = np.zeros((self.gen_num,self.feature_len))  
# 定义一个数组存储每一个点的坐标和其临近点的坐标
self.k_neighbor = np.zeros((self.sample_num,self.k),dtype=int)  

最后一句，如果我们K值设置的是3，也就是寻找最邻近的三个点，若一共有10个数据那就是生成的是一个10×3的全零数组存储的是每一个点的与它最近的三个点的数据所在位置的索引值
例如一个数据为x = [1,4,3,2]
其对应索引值为[0,1,2,3] (x[0] = 1,x[1] = 4, x[2] = 3,x[3] = 2)
k值为2
则计算之后的数组（self.k_neighbor）为
[[3,2],
[2,3],
[1,3],
[0,2]]
标黄意味着 除了x[0] 的三个数中 x[3],x[2]离x[0]最近，x[3]更近一些
（越靠前的越近，同样近的索引值小的靠前）
同理
[[3,2],
[2,3],
[1,3],
[0,2]]
第二行意味着除了x[1] 的三个数中 x[2],x[3]离x[1]最近

2.2计算距离部分

再介绍一下函数有基础可以跳过

2.2.1 enumerate（）

enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标，一般用在 for 循环当中

seasons = ['Spring', 'Summer', 'Fall', 'Winter']
print(list(enumerate(seasons)))
#[(0, 'Spring'), (1, 'Summer'), (2, 'Fall'), (3, 'Winter')]

链接: 菜鸟教程enumerate

2.2.2 numpy.argsort()

numpy.argsort() 函数返回的是数组值从小到大的索引值。

import numpy as np 
x = np.array([3,  1,  2])  
print ('我们的数组是：')
print (x)
print ('\n')
print ('对 x 调用 argsort() 函数：')
y = np.argsort(x)  
print (y)
print ('\n')
print ('以排序后的顺序重构原数组：')
print (x[y])
print ('\n')
print ('使用循环重构原数组：')
for i in y:  
    print (x[i], end=" ")
'''
我们的数组是：
[3 1 2]
对 x 调用 argsort() 函数：
[1 2 0]
以排序后的顺序重构原数组：
[1 2 3]
使用循环重构原数组
1 2 3
'''

链接: 菜鸟教程argsort

2.2.3 numpy.square()

算数组中每一个数的平方

print('sqrt计算各个元素的平方根：')
num = np.array([1,2,3])
print(num)
print(np.square(num))
'''
sqrt计算各个元素的平方根：
[1,2,3]
[1,4,9]
'''

2.2.4 列表生成式(推导式)

Python 推导式是一种独特的数据处理方式，可以从一个数据序列构建另一个新的数据序列的结构体。

'''
[表达式 for 变量 in 列表] 
[out_exp_res for out_exp in input_list]

或者 

[表达式 for 变量 in 列表 if 条件]
[out_exp_res for out_exp in input_list if condition]
'''
multiples = [i for i in range(30) if i % 3 == 0]
print(multiples)
[0, 3, 6, 9, 12, 15, 18, 21, 24, 27]

2.2.5 距离样本代码

好了铺垫完这回再看代码，应该不至于劝退了

    def get_neighbor_point(self):
        for index,single_signal in enumerate(self.sample):
            # 获取欧式距离
            Euclidean_distance = np.array([np.sum(np.square(single_signal-i)) for i in self.sample])
            # 获取欧式距离从小到大的索引排序序列
            Euclidean_distance_index = Euclidean_distance.argsort()
            # 截取k个距离最近的样本的索引值
            self.k_neighbor[index] = Euclidean_distance_index[1:self.k+1]

Euclidean_distance返回的是一个距离数组，计算距离使用欧式距离，也就是对应点的平方求和
Euclidean_distance_index返回的是从小到大的样本距离排序的索引，每个Euclidean_distance_index第一个索引值一定是本次循环的对比信号本身，因为距离是0，所以从列表的第二个数据开始截取K个索引存到最开始定义的self.k_neighbor变量的对应位置中

self.k_neighbor[index] = Euclidean_distance_index[1:self.k+1]

好了终于把计算距离这一部分说完了

2.3 生成数据

铺垫环节

2.3.1 random.randint (a,b)

random.randint(参数1, 参数2)
参数1，参数2必须是整数
函数返回参数1和参数2之间的任意整数

import random
result = random.randint(1,10)
print("result: ",result)
#输出：
#result: 6

2.3.2 random.uniform (a,b)

random.uniform(参数1，参数2) 返回参数1和参数2之间的任意值

import random
result = random.uniform(1,3)
print("result: ",result)
#输出：
#result: 2.639781736005787

2.3.3 生成部分代码

生成代码部分循环self.gen_num次每次的内部步骤都是，选择一个中心样本，然后选择一个他的临近样本，生成合成样本

def get_syn_data(self):
    self.get_neighbor_point()
    #生成self.gen_num个样本循环N次
    for i in range(self.gen_num):
    	#随机选择的中心样本点的索引
        key = random.randint(0,self.sample_num-1)
    	#随机选择的中心样本点的邻近样本点中的随机一个
        K_neighbor_point = self.k_neighbor[key][random.randint(0,self.k-1)]
        #gap = x1-x2 = self.sample[K_neighbor_point]（随机选择的当前样本中前k近的样本点中的随机一个）- self.sample[key]（随机选择的用于生成数据的中心样本点） 
        gap = self.sample[K_neighbor_point] - self.sample[key]
        #公式 生成 = 被选中作为中心的样本 - 0到1中的一个数 × （被选中作为中心的样本 - 被选中作为中心的样本的临近样本点中的随机一个）
        self.syn_data[i] = self.sample[key] + random.uniform(0,1)*gap
        return self.syn_data

---

三.完整代码如下

import numpy as np
import random
import matplotlib.pyplot as plt

class SMOTE(object):
    def __init__(self,sample,k=2,gen_num=3):
        self.sample = sample      
        self.sample_num,self.feature_len = self.sample.shape
        self.k = min(k,self.sample_num-1)                
        self.gen_num = gen_num    
        self.syn_data = np.zeros((self.gen_num,self.feature_len))  
        self.k_neighbor = np.zeros((self.sample_num,self.k),dtype=int)  

    def get_neighbor_point(self):
        for index,single_signal in enumerate(self.sample):
            Euclidean_distance = np.array([np.sum(np.square(single_signal-i)) for i in self.sample])
            Euclidean_distance_index = Euclidean_distance.argsort()
            self.k_neighbor[index] = Euclidean_distance_index[1:self.k+1]

    def get_syn_data(self):
        self.get_neighbor_point()
        for i in range(self.gen_num):
            key = random.randint(0,self.sample_num-1)
            K_neighbor_point = self.k_neighbor[key][random.randint(0,self.k-1)]
            gap = self.sample[K_neighbor_point] - self.sample[key]
            self.syn_data[i] = self.sample[key] + random.uniform(0,1)*gap
        return self.syn_data

if __name__ == '__main__':
    #随机生成原始数据
	data=np.random.uniform(0,1,size=[20,2])
    #生成对象k=5 gen_num=20
    Syntheic_sample = SMOTE(data,5,20)
    #生成数据
    new_data = Syntheic_sample.get_syn_data()
	#绘制原始数据
    for i in data:
        plt.scatter(i[0],i[1],c='b')
	#绘制生成数据
    for i in new_data:
        plt.scatter(i[0],i[1],c='y')
    plt.show()

蓝色是原始样本橘色是生成样本

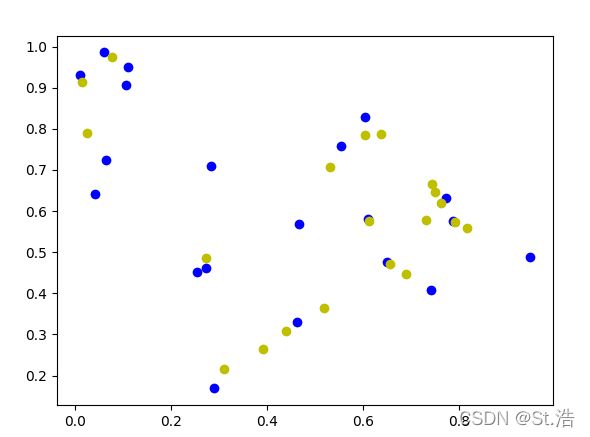
虽然点看着分散，你要是细心观察你会发现所有的橘色的点都在两个蓝色的点的联线上，为清晰这点其实有一个更直观的方法，直接把生成的点选择成好几百，如果k=5 gen_num = 100还是不够明显

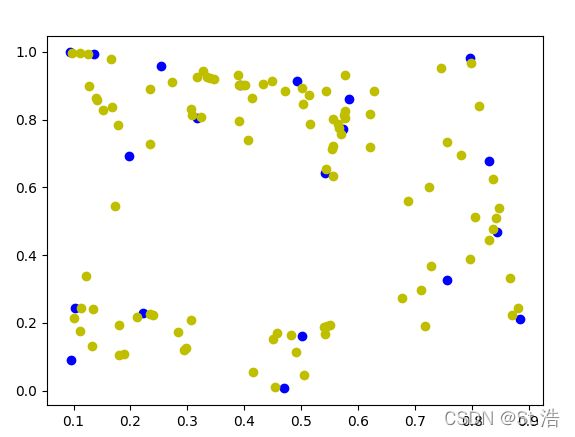
再来个gen_num = 500 的这回生成的样本点在连线上已经很明显了

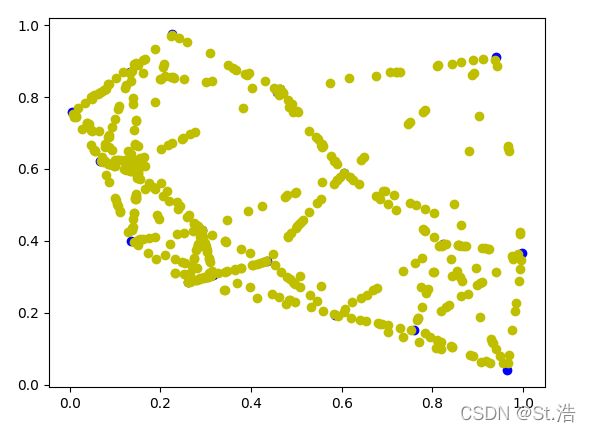
这回将k设置成3同样生成500个样本比起k=5的时候交叉线明显减少了

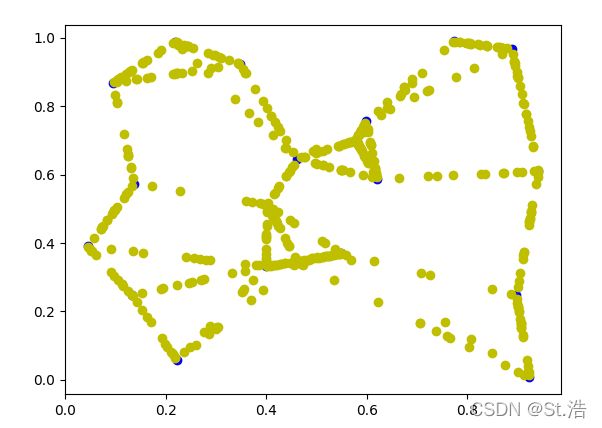
将k设置成1再来一次可以看到生成的样本已经没有交叉线了

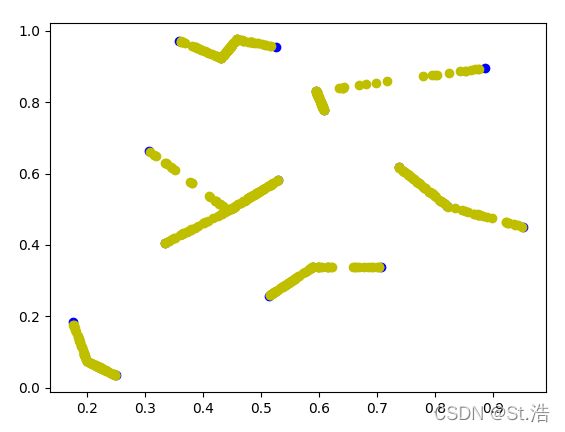
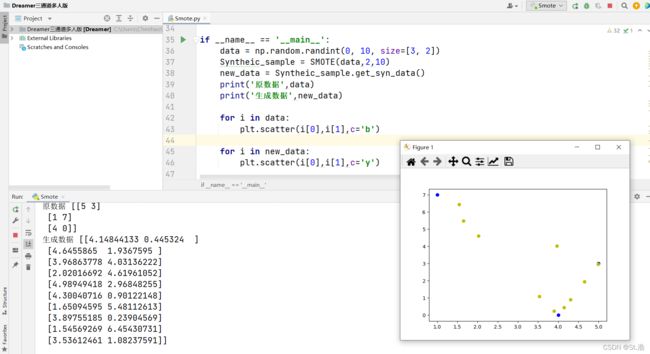
最后再试一下生成整数原始数据，扩充之后将原始数据和生成数据打印出来

总结

这个代码目前只能生成一维的数据，高维的需要处理成一维的才能使用，然后之后会尝试写SMOTE的各种延伸版本
也非常感谢这位老哥的参考
链接: 原版论文复现.