E2-AEN: End-to-End Incremental Learning with Adaptively Expandable Network

前段时间忙着本科毕业工作还有投稿的工作耽搁了，现在开始恢复更新啦～
今天看的一篇是基于动态架构的持续学习论文，论文地址点这里。

一. 介绍

持续学习致力于以增量方式学习新的数据或任务，并且不会出现灾难性遗忘。最早的方法考虑了机遇正则化的策略（如EWC），其通过考虑网络中的重要权重来保存旧知识，但这种方法会使得这些权重无法处理好新的任务。第二种方法是基于记忆重放（GEM），通过保存一部分旧的样再之后配合新样本一起训练，然而如果后续任务的不相关，则模型会陷入stability-plasticity（稳定性-可塑性）问题。最近，参数隔离（如FedWEIT使用了掩码来隔离参数）成为增量学习的新趋势，因为不同的任务可能需要不同的参数或网络结构，从而避免任务之间的干扰。然而，如果要处理大量任务，主干模型的容量往往会饱和，从而限制了增量框架的丰富组合性。

还有一种持续学习的方法称为动态的模型架构，其通过为新任务增加新的分支来进行扩展。早期的动态架构采取固定（线性）增加方式，但这样会增加内存和计算的压力，如下图的(a)。为了改善这样的情况，会对动态的模型进行修剪，如图(b)所示，但这也就导致了其他的问题，例如为了寻找到更好的结构却增大了搜索空间。此外，它们都将学习过程分为多个阶段：首先定义每一个任务的网络进行训练。然后，重新训练策略严重依赖于额外的超参数，导致过多的计算成本。这些方法很难应用于资源受限的场景，如移动设备或视频监控摄像机。

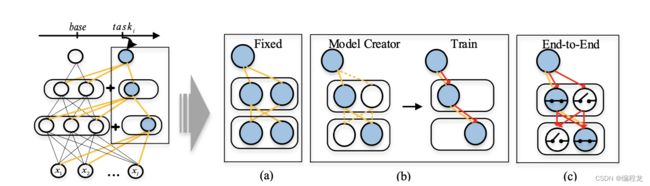
因此一个好的动态架构满足三点：(1) stability-plasticity（稳定性-可塑性）(2) 轻量级的参数规模 (3)较少的额外成本。针对于此本文提出了一种端到端可训练的自适应可扩展网络（E2-AEN），以实现全局优化，如图©。该方法由一系列AES（自适应扩展架构）组成，简单来说就是每个AES能够跟新任务生成新的架构去应对，并且采用高效的方式去实现这个架构。

二.方法

2.1 问题表述

在持续学习中，一系列任务$\{tas{k}_1,...,tas{k}_N\}$逐渐到来。对于每一个任务，数据集可以表示为$D_i=\{x_j,y_j{\}}_{j=1}^{N_i}$，$x_j$表示为原始的数据特征，$y_j$表示每一个数据特征对应的标签，$N_i$表示在第$i$个任务上的数据规模。为了能够不断地学习这些任务，我们的目标可以定义为：$y_i=\Phi (x_i;{\Theta }^s,{\Theta }_i^t)$，其中${\Theta }^s$表示为任务共享参数，${\Theta }_i^t$表示为特定任务参数。因此目标函数可以表示为：
$$\mathcal{L}=\sum _{i=1}^N{\mathcal{L}}_i({\Theta }_i^t;{\Theta }^s,D_i)\text{\hspace{1em}(1)}$$
其中${\mathcal{L}}_i$表示为第$i$个任务的损失函数。

2.2 自适应扩展机制

本文提出的端到端可训练自适应扩展网络（E2-AEN）可以取代基于基本自适应扩展机制的阶段式优化。它是通过一系列称为自适应可扩展结构（AES）的轻量级模块与基础网络一起实现的，对应于下图所示的每个特定任务。AES有两种可能的状态，活动和非活动。当状态处于活动状态时，功能适配器将冻结主干，以适应新任务，否则将跳过特征适配器，从而节省一些不必要的计算和参数，这是自适应和高效的。

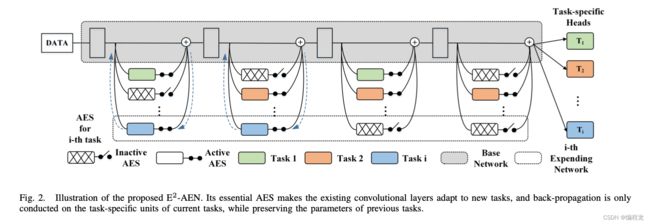
因此给定第$j$个卷积模块$H_j$，那么在第$i$个任务上的第$j$个使用AES的卷积模块的前向传播可以表示为：
$$F_{i,j}=H_j+{\mathcal{A}}_{i,j}(H_j)\text{\hspace{1em}(2)}$$
其中${\mathcal{A}}_{i,j}$是一个可微分的AES模块。

提出的AES有两个关键组件：设计的特征适配器和基于自适应的剪枝策略，如下图所示。功能强大的特征适配器，其操作表示为$\mathcal{D}(\cdot )$，负责将先前学习的表示扩展到新概念空间，并有效避免任务干扰。它使得主干参数被冻结，因此在之前的任务中不会出现遗忘现象。基于自适应门的修剪策略(gate-based)致力于减少特征适配器带来的冗余参数，使框架更高效，其操作表示为$\mathcal{G}(\cdot )$。得益于基于门的修剪策略(gate-based)，AES能够确定是否需要在某个卷积层中执行功能适配器，还是可以跳过它，因此(2)可以变为：
$$F_{i,j}=H_j+{\mathcal{G}}_{i,j}({\mathcal{D}}_{i,j}(H_j))\cdot {\mathcal{D}}_{i,j}(H_j)\text{\hspace{1em}(2)}$$
其中$\mathcal{G}(\cdot )\in \{0,1\}$。

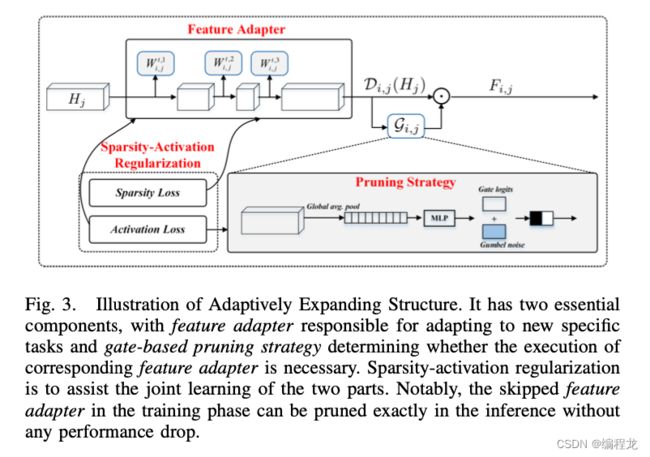
• (1) 特征适配器： 如上面所述，特征适配器将原始的输出扩展到新的输出空间，表示为：
  $$\begin{array}{rl}{E}_{i,j}& =H_j+{\mathcal{D}}_{i,j}(H_j)\\ & =H_j+\sigma ({\Theta }_{i,j}^{t,3}\otimes \sigma ({\Theta }_{i,j}^{t,2}\otimes \sigma ({\Theta }_{i,j}^{t,1}\otimes H_j)))\end{array}\text{\hspace{1em}(3)}$$
  如果$H_j$的通道大小表示为$c$，则${\Theta }_{i,j}^{t,1}\in {\mathbb{R}}^{c\ast \frac{c}{3}}$，${\Theta }_{i,j}^{t,2}\in {\mathbb{R}}^{\frac{c}{3}\ast \frac{c}{6}}$，${\Theta }_{i,j}^{t,3}\in {\mathbb{R}}^{\frac{c}{6}\ast c}$。$\sigma$表示为RELU函数，$\otimes$表示为卷积操作。${\Theta }_{i,j}^{t,1}$和${\Theta }_{i,j}^{t,3}$的kernel大小都为1x1，${\Theta }_{i,j}^{t,2}$为3x3。注意，每次卷积之后都需要进行BathNormalization。
• (2) 自适应的基于门的修剪策略： 在前向传播过程中，基于门的修剪策略通过全局平均池学习理解特征适配器的特征，以捕获卷积特征中的丰富信息，同时保持计算效率。之后连接上两个带RELU激活函数的全连接层。为了能够控制每一个AES块的选取，采用了二进制的方式进行判断。然而这就导致了函数存在不可微分的现象，因此使用Gumbel-softmax进行处理。具体来说，Gumbel-Max 将我们的概率分布$v_{i,j}$转换为如下：
  $$z_{i,j}=\underset{k\in \{0,1\}}{\mathrm{argmax}}[log{v}_{i,j}(k)+g_{i,j}]\text{\hspace{1em}(4)}$$
  其中$k$表示门的选择，0表示不激活1表示激活。$v_{i,j}(k)$表示激活的概率组合，也就是$[{\alpha }_{i,j},1-{\alpha }_{i,j}]$，$g_{i,j}$表示为一个Gumbel分布。（这里其实大致意思还是softmax，只是为了避免不可微分的情况，在softmax上增加了一个特殊的分布，具体可以搜索一下不是很复杂，就不解释了）。
• (3)稀疏-激活 正则化：为了能使得整个网络在端到端都能适应，本文在损失函数上进行了优化。
  稀疏约束： 为了减少AES中的冗余参数，设定了一个目标函数：
  $${\mathcal{L}}_{sparse}=\sum _{j=1}^L\sqrt{\sum _{k=1}^{|{\Omega }_j|}({\theta }_{j,k}{)}^2}\text{\hspace{1em}(5)}$$
  其中$L$表示在第$i$个任务的特征适配器的个数，${\Omega }_j=\{{\Theta }_{i,j}^{t,1},{\Theta }_{i,j}^{t,2},{\Theta }_{i,j}^{t,3}\}$。
  激活约束： 基于门的剪枝策略根据新的自适应特征的复杂性来确定每个特征适配器对某一层是否是必需的，即当其对应的特征适配器的稀疏度很小时，自适应特征就会很简单，因此对该特征适配器的剪枝实际上不会带来很大的性能下降。换句话说，当特性适配器非常稀疏时，(3)中的门${\mathcal{G}}_{i,j}$应该被禁用，反之亦然。因此第$j$层的稀疏性定义为有效权重的比例：
  $${\mathcal{R}}_j^s=\mathbb{P}[|{\theta }_{j,k}|\ge \sigma ],k\in 1,2,...,|{\Omega }_j|\text{\hspace{1em}(6)}$$
  其中$\mathbb{P}[.]$表示为在${\Omega }_j$中权值大于$\sigma$的比例。接下来，我们需要定义另一个损失块称为激活占比：
  $${\mathcal{R}}_j^a=\frac{{\sum }_{k=1}^{|B|}{\mathcal{G}}_{i,j}^k(D_{i,j}(H_j^k))}{|B|}\text{\hspace{1em}(7)}$$
  其中$|B|$表示一个batch的数目。因此，激活正则化约束可以表示为：
  $${\mathcal{L}}_{active}=\frac{1}{L}\sum _{j=1}^L||{\mathcal{R}}_j^s-{\mathcal{R}}_j^a|{|}_2^2\text{\hspace{1em}(8)}$$
  因此本文的损失函数可以描述为：
  $${\mathcal{L}}_i={\mathcal{L}}_{ce}+{\lambda }_s{\mathcal{L}}_{sparse}+{\lambda }_a{\mathcal{L}}_{active}\text{\hspace{1em}(10)}$$

三. 方法的一些理解

在看论文中发现作者对很多地方都添加了东西，为了方便理解我这里简单的说明一下。首先本文是基于动态架构的持续学习，因此每一个任务到来时都会有生成新的空间给他训练，在训练过程中作者设计了一个门的结构，也就是不是每次都添加所有的层（这里所有的层指的是所有的CNN）。因此现在就有两个问题：一是如何添加层，二是如何控制每个任务选择不同的层。首先第一个问题，作者在每一个CNN上连接了一个特殊的卷积块，基本的卷积块加上这一部分形成了新的空间——该任务的特征空间；第二问题则是会对添加的这一部分转换成一个0或1的值，经过转换后来确定是否进行激活。上述两个问题分别对应于特质适配器和自适应门修剪。为了进一步缩小使用量，作者在损失函数上添加了其余的东西。首先作者说明可以对特征适配器上的参数进行修剪，这里就是尽量使得整个参数稀疏，因此损失定义如(5)所示。紧接着，既然每一个任务适配器的参数稀疏度都不一样，那么就可以根据稀疏度来决定是否激活（也就是越稀疏越不希望被激活），因此设定了第二个损失函数，可以发现它包括两部分：一个是判断这个参数的稀疏度，另一个是在使用自适应门修剪时具体数据的激活情况，尽量让其相等。举个例子：总共5张图片，假如在某一个块中我们的稀疏度为0.4的话，而在这个快却有4张照片被激活，激活概率为4/5=0.8，表明此时我们的稀疏度特别高，不应该能激活那么多，所以尽量使其两个值相等。作者最后还说了一些具体训练推理的东西，由于没有找到源码就不进行说明了，等我找到了我就配合源代码进行解析。