MATLAB求解方程和多元方程组

0. 说明

前面有两篇博文分别介绍了：

MATLAB求常微分方程的解析解
MATLAB求常微分方程的数值解

为了形成一个体系，我决定把普通方程组的求解也介绍一下。

本博文也是按照MATLAB的官方文档展开的（推荐大家多看官方文档）

1. 核心函数solve

一般形式 S=solve(eqns,vars,Name,Value) ，其中：

eqns是需要求解的方程组；
vars是需要求解的变量；
Name-Value对用于指定求解的属性（一般用不到）；
S是结果，对应于vars中变量；

2. 单个方程求解

方程：sin(x)=1
代码：

syms x; %定义x是一个未知量
eqn=sin(x)==1; % 定义方程，eqn只是一个代号，代表sin(x)==1
solX=solve(eqn,x) % 求方程eqn中的x，放入solX中

结果：

说明： MATLAB定义方程用的是 == 符号，就是这样规定的哈。

注意： 细心的同学应该发现了，本例的解实际上应该是 pi/2+2k*pi ，怎么得到呢？
添加Name-Value对即可解决，输入以下代码：

syms x; %定义x是一个未知量
eqn=sin(x)==1; % 定义方程，eqn只是一个代号，代表sin(x)==1
[solX,params,cond]=solve(eqn,x,'ReturnConditions',true) % 求方程eqn中x的所有解，放入solX中,params是参数，cond存储参数性质

得到理想结果：

3. 带未知参数的方程

方程： ax²+bx+c=0
代码：

syms x a b c; %定义x a b c是未知量
eqn=a*x^2+b*x+c==0;% 定义方程
solX=solve(eqn,x) % 解方程

结果：

说明： 这里就简单的把未知参数用syms声明就可以了。

4. 多元方程组求解

方程：

代码：

syms u v; % 定义u v 是未知量
eqns=[2*u+v==0,u-v==1]; % 定义方程组
vars=[u,v]; % 定义求解的未知量
[solU,solV]=solve(eqns,vars) % 求解eqns中的vars未知量，分别存储
sol=solve(eqns,vars); % 求解eqns中的vars未知量，以结构体的形式存储到sol中
solU1=sol.u % 从sol结构体中取出变量u的解
solV1=sol.v % 从sol结构体中取出变量v的解

结果：

说明： 本例中有两个求解的变量，有两种存储方式，已在代码中介绍。

5. 数值近似解

方程： sin(x)==x²-1
代码：

syms x; % 定义x是未知量
fplot(sin(x),[-2,2]); % 绘制y=sin(x)的图像
hold on; 
fplot(x^2-1,[-2,2]); % 绘制y=x^2-1的图像
hold off;
eqn=sin(x)==x^2-1; % 定义方程
solX=solve(eqn,x) % 直接求解，返回其找到的第一个数值近似解
solX1=vpasolve(eqn,x,[0,2]) % vpa求解，返回其在范围[0,2]内找到的第一个数值近似解

结果：


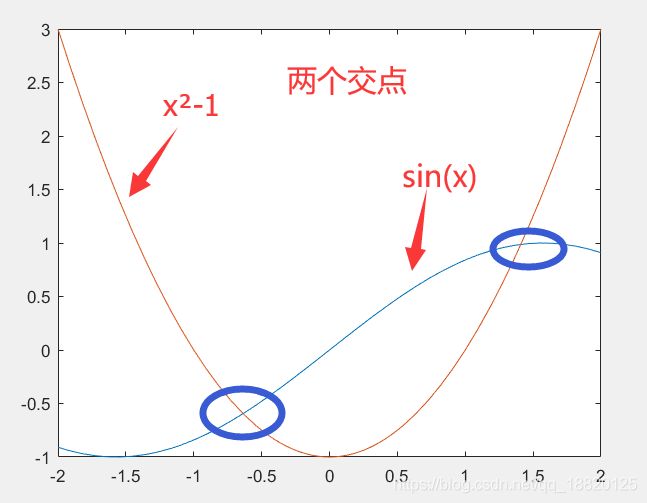
说明： 此例中无法求得精确解，slove会返回求得的第一个数值近似解，vpasolve可以返回指定范围内第一个近似解

6. 无解的情况

方程：

代码：

syms x; % 定义x是未知量
eqn=[3*x+2==0,3*x+1==0]; % 定义函数
solX=solve(eqn,x) % 求解

结果：

7. 多多留言点赞！