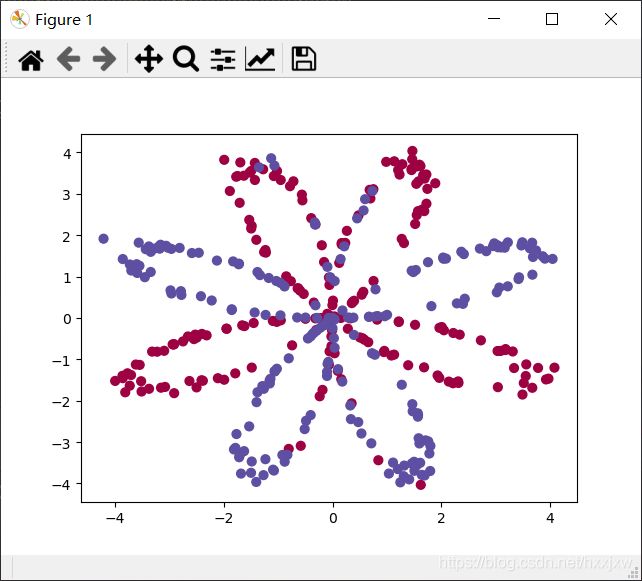
通过例子来感受神经网络的优越 (logistic 回归 vs 神经网络)

处理一个二分类问题

用logistic回归(sigmoid)来解决

import torch
import numpy as np
from torch import nn
from torch.autograd import Variable
import torch.nn.functional as F

import matplotlib.pyplot as plt

def plot_decision_boundary(model, x, y):
    # Set min and max values and give it some padding
    x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
    y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole grid
    Z = model(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the 轮廓 and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.ylabel('x2')
    plt.xlabel('x1')
    plt.scatter(x[:, 0], x[:, 1], c=y.reshape(-1), s=40, cmap=plt.cm.Spectral)

np.random.seed(1)
m = 400 # 样本数量
N = int(m/2) # 每一类的点的个数
D = 2 # 维度
x = np.zeros((m, D))
y = np.zeros((m, 1), dtype='uint8') # label 向量，0 表示红色，1 表示蓝色
#x都是float
#y都是int

a = 4



for j in range(2):
    ix = range(N*j,N*(j+1))   #ix=range(0, 200) ,  range(200,400)
    t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta
    r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius
    x[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
    y[ix] = j


plt.scatter(x[:, 0], x[:, 1], c=y.reshape(-1), s=40, cmap=plt.cm.Spectral)
plt.show()



#尝试用 logistic 回归来解决这个问题
def logistic_regression(x):
    return torch.mm(x, w) + b

def plot_logistic(x):
    x = Variable(torch.from_numpy(x).float())
    out = F.sigmoid(logistic_regression(x))
    out = (out > 0.5) * 1
    return out.data.numpy()


x = torch.from_numpy(x).float()
y = torch.from_numpy(y).float()


w = nn.Parameter(torch.randn(2, 1))
b = nn.Parameter(torch.zeros(1))


optimizer = torch.optim.SGD([w, b], 1e-1)


criterion = nn.BCEWithLogitsLoss()

#这是先把模型训练一波
for e in range(100):
    out = logistic_regression(Variable(x))
    loss = criterion(out, Variable(y))
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if (e + 1) % 20 == 0:
        print('epoch: {}, loss: {}'.format(e+1, loss.item()))


plot_decision_boundary(lambda x: plot_logistic(x), x.numpy(), y.numpy())
plt.title('logistic regression')
# Text(0.5,1,'logistic regression')
plt.show()

可以看到，logistic 回归并不能很好的区分开这个复杂的数据集

logistic回归只是一个线性分类器

用神经网络来解决

import torch
import numpy as np
from torch import nn
from torch.autograd import Variable
import torch.nn.functional as F

import matplotlib.pyplot as plt

def plot_decision_boundary(model, x, y):
    # Set min and max values and give it some padding
    x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
    y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    # Predict the function value for the whole grid
    Z = model(np.c_[xx.ravel(), yy.ravel()])
    print(Z)
    Z = Z.reshape(xx.shape)
    print(Z)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.ylabel('x2')
    plt.xlabel('x1')
    plt.scatter(x[:, 0], x[:, 1], c=y.reshape(-1), s=40, cmap=plt.cm.Spectral)

np.random.seed(1)
m = 400 # 样本数量
N = int(m/2) # 每一类的点的个数
D = 2 # 维度
x = np.zeros((m, D))
y = np.zeros((m, 1), dtype='uint8') # label 向量，0 表示红色，1 表示蓝色
a = 4

for j in range(2):
    ix = range(N*j,N*(j+1))
    t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta
    r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius
    x[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
    y[ix] = j

plt.scatter(x[:, 0], x[:, 1], c=y.reshape(-1), s=40, cmap=plt.cm.Spectral)
plt.show()


#利用神经网络来解决
x = torch.from_numpy(x).float()
y = torch.from_numpy(y).float()

# 定义两层神经网络的参数
w1 = nn.Parameter(torch.randn(2, 4) * 0.01) # 隐藏层神经元个数 2
b1 = nn.Parameter(torch.zeros(4))

w2 = nn.Parameter(torch.randn(4, 1) * 0.01)
b2 = nn.Parameter(torch.zeros(1))

# 定义模型
def two_network(x):
    x1 = torch.mm(x, w1) + b1
    x1 = F.tanh(x1) # 使用 PyTorch 自带的 tanh 激活函数
    x2 = torch.mm(x1, w2) + b2
    return x2

def plot_network(x):
    x = Variable(torch.from_numpy(x).float())
    x1 = torch.mm(x, w1) + b1
    x1 = F.tanh(x1)
    x2 = torch.mm(x1, w2) + b2
    out = F.sigmoid(x2)
    out = (out > 0.5) * 1
    return out.data.numpy()


optimizer = torch.optim.SGD([w1, w2, b1, b2], lr=1.)

criterion = nn.BCEWithLogitsLoss()

# 我们训练 10000 次
for e in range(10000):
    out = two_network(Variable(x))
    loss = criterion(out, torch.tensor(y))
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if (e + 1) % 1000 == 0:
        print('epoch: {}, loss: {}'.format(e+1, loss.item()))




plot_decision_boundary(lambda x: plot_network(x), x.numpy(), y.numpy())
plt.title('2 layer network')
plt.show()

可以看到神经网络能够非常好地分类这个复杂的数据，和前面的 logistic 回归相比，神经网络因为有了激活函数的存在，成了一个非线性分类器，所以神经网络分类的边界更加复杂。