keras Conv2D参数详解
Conv2D layer 二维卷积层
本文是对keras的英文API DOC的一个尽可能保留原意的翻译和一些个人的见解,会补充一些对个人对卷积层的理解。这篇博客写作时本人正大二,可能理解不充分。
Conv2D class
tf.keras.layers.Conv2D(
filters,
kernel_size,
strides=(1, 1),
padding="valid",
data_format=None,
dilation_rate=(1, 1),
groups=1,
activation=None,
use_bias=True,
kernel_initializer="glorot_uniform",
bias_initializer="zeros",
kernel_regularizer=None,
bias_regularizer=None,
activity_regularizer=None,
kernel_constraint=None,
bias_constraint=None,
**kwargs
)
二维卷积层(例如空间卷积图像)。
这一层创建了一个卷积核,它与这一层的输入卷积以产生一个输出张量。
如果 use_bias为真,则创建一个偏差向量并添加到输出中。
最后,如果activation不是None,它也应用于输出。
当使用此层作为模型的第一层时,提供关键字参数input_shape(整数元组,不包括样本轴(不需要写batch_size)),例如。
input_shape=(128, 128, 3)表示 128x128的 RGB 图像data_format="channels_last"
这个data_format参数是这样影响input_shape工作的如果不填写,默认是channels_last,否则可以填写channels_first。前者的会把input_shape这个三元组给识别成(batch_size, height, width, channels),后者则会识别成(batch_size, channels, height, width)不过样本轴不需要自己填写(不然反而会报错)
Examples
>>> # The inputs are 28x28 RGB images with `channels_last` and the batch
>>> # size is 4.
>>> input_shape = (4, 28, 28, 3)
>>> x = tf.random.normal(input_shape)
>>> y = tf.keras.layers.Conv2D( ...
2,3,activation='relu',input_shape=input_shape[1:])(x)
>>> print(y.shape) (4, 26, 26, 2)
>>> # With `dilation_rate` as 2.
>>> input_shape = (4, 28, 28, 3)
>>> x = tf.random.normal(input_shape)
>>> y = tf.keras.layers.Conv2D( ...
2,3,activation='relu',dilation_rate=2,input_shape=input_shape[1:])(x)
>>> print(y.shape) (4, 24, 24, 2)
>>> # With `padding` as "same".
>>> input_shape = (4, 28, 28, 3)
>>> x = tf.random.normal(input_shape)
>>> y = tf.keras.layers.Conv2D( ...
2, 3, activation='relu', padding="same", input_shape=input_shape[1:])(x)
>>> print(y.shape) (4, 28, 28, 2)
>>> # With extended batch shape [4, 7]:
>>> input_shape = (4, 7, 28, 28, 3)
>>> x = tf.random.normal(input_shape)
>>> y = tf.keras.layers.Conv2D( ...
2, 3, activation='relu', input_shape=input_shape[2:])(x)
>>> print(y.shape) (4, 7, 26, 26, 2)
参数[以下方框内注释内容为个人理解,仅供参考]
-
filters: 整数,输出空间的维数(即在卷积中输出滤波器的数量)。[注:此处认为是与input_shape的通道数一样,比如是RGB就是3,是灰度图就是1]
-
kernel_size:一个整数或2个整数的元组/列表,指定二维卷积窗口的高度和宽度。
可以是单个整数,为所有空间维度指定相同的值。 -
strides: 一个整数或两个整数的元组/列表,指定沿高度和宽度的卷积的步长。可以是单个整数,为所有空间维度指定相同的值。
指定任何strides值!= 1与指定任何dilation_rate值!= 1是不兼容的。 -
padding: one of
"valid"or"same"(不区分大小写).[注:卷积会导致输出图像越来越小,图像边界信息丢失,若想保持卷积后的图像大小不变,需要设置padding参数为same] -
data_format: 一个字符串参数, 要么是
channels_last(默认) ,要么就是channels_first. 是输入的维度顺序排列理解。channels_last对应着(batch_size, height, width, channels),而channels_first对应的输入为(batch_size, channels, height, width). 他默认为 在~/.keras/keras.json.中的image_data_format的值 如果你不设置这个地方,它就会是channels_last. -
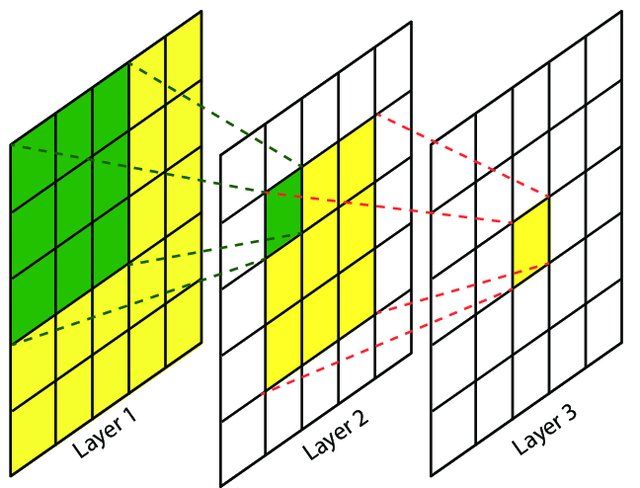
dilation_rate: 一个整数或两个整数的元组/列表,指定用于扩展卷积的扩展率。可以是单个整数,为所有空间维度指定相同的值。该参数定义了卷积核处理数据时各值的间距。 在相同的计算条件下,该参数提供了更大的感受野。该参数经常用在实时图像分割中。当网络层需要较大的感受野,但计算资源有限而无法提高卷积核数量或大小时,可以考虑使用。
下图为卷积核为3,扩展率为2的和没有padding的二维卷积
-
groups: A positive integer specifying the number of groups in which the input is split along the channel axis. Each group is convolved separately with
filters / groupsfilters. The output is the concatenation of all thegroupsresults along the channel axis. Input channels andfiltersmust both be divisible bygroups. -
activation: 使用激活函数。 如果不特别指定,将不会使用任何的激活函数 ( 具体的可选项可以参考
keras.activations). -
use_bias: Boolean类型, 这一层是否有bias单元.
-
kernel_initializer: 默认是
GlorotUniform,通过输入和输出单元个数来推演权重矩阵尺寸 ( 可选项在keras.initializers). -
bias_initializer:
kernelbias单元的初始化器,默认是0 ( 可选项在keras.initializers). -
kernel_regularizer: Regularizer function applied to the
kernelweights matrix (seekeras.regularizers). -
bias_regularizer: Regularizer function applied to the bias vector ( see
keras.regularizers). -
activity_regularizer: Regularizer function applied to the output of the layer (its “activation”) ( see
keras.regularizers). -
kernel_constraint: Constraint function applied to the kernel matrix ( see
keras.constraints). -
bias_constraint: Constraint function applied to the bias vector ( see
keras.constraints).
Returns
一个四阶张量 activation(conv2d(inputs, kernel) + bias).
Raises
- ValueError: if
paddingis"causal". - ValueError: 当
strides > 1而且dilation_rate > 1.
卷积层的卷积核大小为什么要大于1?
为了有感受野这一个东西存在。
为什么卷积核都是奇数的?
因为即使有padding=same的情况下,他不能保证输入的尺寸等于输出的尺寸
是不是越大的卷积核大小越好?
在达到相同感受野的情况下,卷积核越小,计算量越小,一般用的都是3X3
I n p u t = ( C i n ( 通 道 数 ) , H i n ( 高 ) , W i n ( 宽 ) ) Input=(Cin(通道数),Hin(高),Win(宽)) Input=(Cin(通道数),Hin(高),Win(宽))
K e r n e l = ( K w ( 卷 积 核 的 宽 ) , K h ( 高 ) ) Kernel=(Kw(卷积核的宽),Kh(高)) Kernel=(Kw(卷积核的宽),Kh(高))
P a d d i n g = ( 0 ∣ 1 ) Padding=(0|1) Padding=(0∣1)
$Strides= $ 这个定不了所以留空
H o u t ( 输 出 层 图 像 的 高 ) = H i n − K h + 2 P S + 1 Hout(输出层图像的高)=\displaystyle\frac{Hin-Kh+2P}{S}+1 Hout(输出层图像的高)=SHin−Kh+2P+1
输出层图像的宽可以类比。
C o u t ( 输 出 的 通 道 数 ) = 上 面 f l i t e r s 参 数 的 个 数 Cout(输出的通道数)=上面fliters参数的个数 Cout(输出的通道数)=上面fliters参数的个数
W e i g h t s P a r a m s = K w ∗ K h ∗ C i n ∗ C o u t Weights\ Params=Kw* Kh *Cin*Cout Weights Params=Kw∗Kh∗Cin∗Cout
B i a s P a r a m s = C o u t Bias\ Params=Cout Bias Params=Cout
F e a t u r e m a p : i n p u t = H i n ∗ W i n ∗ C i n Feature \ map:input=Hin*Win*Cin Feature map:input=Hin∗Win∗Cin
O u t p u t = H o u t ∗ W o u t ∗ C o u t Output=Hout*Wout*Cout Output=Hout∗Wout∗Cout