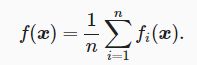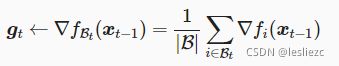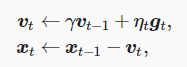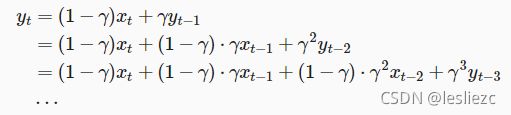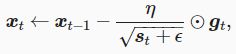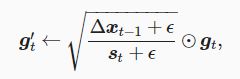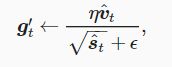Mxnet优化算法学习
一、梯度下降和随机梯度下降
在深度学习里,目标函数通常是训练数据集中有关各个样本的损失函数的平均。设fi(x)是有关索引为i的训练数据样本的损失函数,n是训练数据样本数,x是模型的参数向量,那么目标函数定义为
目标函数在x处的梯度计算为
随机梯度下降(SGD)减少了每次迭代的计算开销。在随机梯度下降的每次迭代中,随机均匀采样的一个样本索引i∈{1,…,n},并计算梯度∇fi(x)来迭代x
而且,随机梯度∇fi(x)∇fi(x)是对梯度∇f(x)的无偏估计
二、小批量随机梯度下降
小批量随机梯度下降随机均匀采样一个由训练数据样本索引组成的小批量Bt,使用
来计算时间步t的小批量Bt上目标函数位于xt−1处的梯度gt,小批量随机梯度gt也是对梯度∇f(xt−1)的无偏估计,小批量随机梯度下降对自变量的迭代如下
Mxnet实现:
train_gluon_ch7('sgd', {'learning_rate': 0.05}, features, labels, 10)其中,batch_size=10
三、动量法
梯度下降法的缺点:自变量的迭代方向仅仅取决于自变量当前位置,对于二维平面,如果目标函数在水平方向和竖直方向的斜率的绝对值相差的很大,较小的学习率会导致收敛变慢,而较大的学习率则可能导致自变量在斜率绝对值较大的方向上越过最优解而逐渐发散
动量法使用了指数加权移动平均的思想。它将过去时间步的梯度做了加权平均,且权重按时间步指数衰减,使得相邻时间步的自变量更新在方向上更加一致
设时间步t的自变量为xt,学习率为ηt。 在时间步0,动量法创建速度变量v0,并将其元素初始化成0。在时间步t>0,动量法对每次迭代的步骤做如下修改
指数加权移动平均 :当前时间步t的变量yt是上一时间步t−1的变量yt−1和当前时间步另一变量xt的线性组合
我们可以对yt展开:
由数学推导可知,可以在近似中忽略所有含γ高阶的系数的项,将yt看作是对最近1/(1−γ)个时间步的xt值的加权平均
现在,将动量法的速度变量的迭代改写为
可近似为梯度gt的指数加权移动平均,所以,在动量法中,自变量在各个方向上的移动幅度不仅取决于当前梯度,还取决于过去的各个梯度在各个方向上是否一致。针对上述梯度下降的缺点,我们可以使用较大的学习率去加速收敛
Mxnet实现:
d2l.train_gluon_ch7('sgd', {'learning_rate': 0.004, 'momentum': 0.9}, features, labels)其中,momentum即为γ
四、AdaGrad算法
AdaGrad算法会使用一个小批量随机梯度gt按元素平方的累加变量st。在时间步0,AdaGrad将s0中每个元素初始化为0。在时间步t,首先将小批量随机梯度gt按元素平方后累加到变量st:
⊙为按元素相乘。接着,将目标函数自变量中每个元素的学习率通过按元素运算重新调整一下
ϵ是为了维持数值稳定性而添加的常数,如1e−6
特点:①AdaGrad算法在迭代过程中不断调整学习率,并让目标函数自变量中每个元素都分别拥有自己的学习率;
②使用AdaGrad算法时,自变量中每个元素的学习率在迭代过程中一直在降低(或不变),在迭代后期由于学习率过小,可能较难找到一个有用的解
Mxnet实现:
d2l.train_gluon_ch7('adagrad', {'learning_rate': 0.1}, features, labels)五、RMSProp算法
RMSProp算法使用了小批量随机梯度按元素平方的指数加权移动平均来调整学习率
ϵ是为了维持数值稳定性而添加的常数,如1e−6
RMSProp算法的状态变量st是对平方项gt⊙gt的指数加权移动平均,所以可以看作最近1/(1−γ)个时间步的小批量随机梯度平方项的加权平均。如此一来,自变量每个元素的学习率在迭代过程中就不再一直降低(或不变)。
Mxnet实现:
d2l.train_gluon_ch7('rmsprop', {'learning_rate': 0.01, 'gamma1': 0.9}, features, labels)六、AdaDelta算法
AdaDelta算法没有学习率超参数,它通过使用有关自变量更新量平方的指数加权移动平均的项来替代RMSProp算法中的学习率
ϵ是为了维持数值稳定性而添加的常数,如1e−5
更新自变量
使用Δxt来记录自变量变化量gt′按元素平方的指数加权移动平均
Mxnet实现:
d2l.train_gluon_ch7('adadelta', {'rho': 0.9}, features, labels)七、Adam算法
Adam算法在RMSProp算法的基础上对小批量随机梯度也做了指数加权移动平均,同时使用了偏差修正
时间步t的动量变量vt即小批量随机梯度gt的指数加权移动平均(β1建议设为0.9)
小批量随机梯度按元素平方的指数加权移动平均变量st(β1建议设为0.999)
当t较小时,过去各时间步小批量随机梯度权值之和会较小(vt的近似),为了消除这样的影响,对于任意时间步t,我们可以将vt再除以1−βt1,从而使过去各时间步小批量随机梯度权值之和为1,这也叫作偏差修正
然后将模型参数中每个元素的学习率通过按元素运算重新调整为
ϵ是为了维持数值稳定性而添加的常数,如1e−8。最后,使用g′tgt′迭代自变量
Mxnet实现:
d2l.train_gluon_ch7('adam', {'learning_rate': 0.01}, features, labels)