简介
对于具有复杂约束-偏微分方程的问题,传统的方法主要依赖自伴随算子,随着深度学习方法的发展,许多基于神经网络的方法也开始出现,这些方法的核心是使用神经网络进行推理的加速,以实现几十倍甚至几百倍的提速,这是相较于传统方法的优势,劣势就是精度不够。深度学习就是这种取舍,通过深度学习来克服传统方法的一些不足,但是其自身也会有诸多问题,可解释性、计算复杂度和推理速度等,从目前来看基于物理机器学习的方法在最优控制问题上具有极强的潜力。
本文介绍的方法是来源于上面两种方法的延伸,也可以是看作算子学习理论的拓展,结合了双层优化理论,这算是一个创新,效果相交于目前的方法还是有长足的进步
Hao, Z., Ying, C., Su, H., Zhu, J., Song, J., & Cheng, Z. (2022). Bi-level Physics-Informed Neural Networks for PDE Constrained Optimization using Broyden's Hypergradients. arXiv preprint arXiv:2209.07075.
传统的自伴随方法可以参考以下的文章:
Xu, S., Li, Y., Huang, X., & Wang, D. (2021). Robust Newton–Krylov Adjoint Solver for the Sensitivity Analysis of Turbomachinery Aerodynamics. AIAA Journal, 59(10), 4014-4030.
Xu, S., Radford, D., Meyer, M., & Müller, J. D. (2015). Stabilisation of discrete steady adjoint solvers. Journal of computational physics, 299, 175-195.
Xu, S., & Timme, S. (2017). Robust and efficient adjoint solver for complex flow conditions. Computers & Fluids, 148, 26-38.
目前解决偏微分方程约束的最优化问题可以参考一下三篇论文:
这一篇的思路是直接暴力优化,效果较差:
Mowlavi, S., & Nabi, S. (2021). Optimal control of PDEs using physics-informed neural networks. arXiv preprint arXiv:2111.09880.
这两篇的思路就是将问题转化为无约束问题并借助梯度下降方法进行求解:
Hwang, R., Lee, J. Y., Shin, J. Y., & Hwang, H. J. (2022, June). Solving pde-constrained control problems using operator learning. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 36, No. 4, pp. 4504-4512).
Wang, S., Bhouri, M. A., & Perdikaris, P. (2021). Fast PDE-constrained optimization via self-supervised operator learning. arXiv preprint arXiv:2110.13297.
问题描述
首先我们考虑以下的问题:
$$ \begin{matrix} \min_{y\in Y_{\mathrm{ad}},u\in U_{\mathrm{ad}}}& \mathcal{J} (y,u)\\ \,\,\mathrm{s}.\mathrm{t}.& \begin{array}{c} \mathcal{F} (y,u)(x)=0,\forall x\in \Omega\\ \mathcal{B} (y,u)(x)=0,\forall x\in \partial \Omega\\ \end{array}\\ \end{matrix} $$
这个时候算子学习就开始发挥作用了,我们分别使用两个神经网络对控制输入\(u\)和对应的偏微分方程约束的解\(y\),分别是\(u_\theta\)和\(y_w\)。这里引入了两层优化的思想,也就是\(u_\theta\)和\(y_w\)是相互影响的,但是一起优化又会造成性能退化。因为损失函数的大小并不是在一个量级,会造成对算子学习或者优化过程至少一个会失败,因此,可以将问题投影为以下的形式:
$$ \begin{array}{ll} \min _\theta & \mathcal{J}\left(w^\star, \theta\right) \\ \text { s.t. } & w^\star=\arg \min _w \mathcal{E}(w, \theta) . \end{array} $$
其中\( \mathcal{E}=\int_{\Omega}\left|\mathcal{F}\left(y_w, u_\theta\right)(x)\right|^2 \mathrm{~d} x+\int_{\partial \Omega}\left|\mathcal{B}\left(y_w, u_\theta\right)(x)\right|^2 \mathrm{~d} x\)。
这个优化的步骤如下:
- 外层优化过程:固定\(\theta\),用梯度下降方法更新\(w\)
- 内层优化过程:固定\(w\),用梯度下降方法更新\(\theta\)
这个过程可以看作是博弈的过程,可以参考双层优化的综述
Liu, R., Gao, J., Zhang, J., Meng, D., & Lin, Z. (2021). Investigating bi-level optimization for learning and vision from a unified perspective: A survey and beyond. IEEE Transactions on Pattern Analysis and Machine Intelligence.
算法细节
算法的具体过程如下图所示: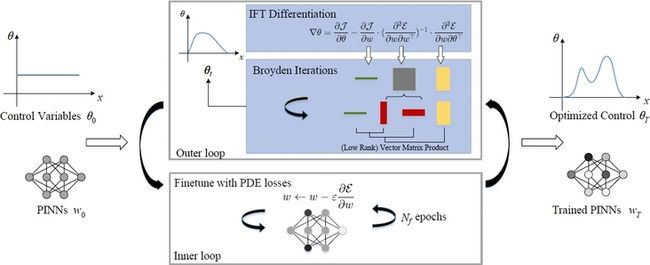
需要指出的是,在算子学习的过程,也即是内层优化\(w\)时,梯度下降与参数\(\theta\)无关。但是在外层优化\(\theta\)时,梯度下降同时依赖两个参数,下面就要介绍为什么是这个形式。
首先考虑这个优化过程,下面我用一张图来形容
$$ u_{\theta}\rightarrow y_w\rightarrow \mathcal{E} \\ u_{\theta}\rightarrow y_{w^\star}\rightarrow \mathcal{J} \left( w,\theta \right) $$
按照这个链式法则就能清晰了,双层优化的内环或者外环过程中,我们固定了一个参数,只用梯度下降更新另一个参数。对于\(w\)的优化,由于链式法则终止于\(w\)自身,那么是不用考虑\(\theta\),但是\(\theta\)的优化就会涉及到\(w\),那么就必须考虑到\(w\)在链式法则中的作用,因此,下面介绍了对\(\theta\)的梯度优化。
具体而言,外层优化目标\( \mathcal{J}\left(w^\star, \theta\right) \)内层优化的最优参数\(w^\star\)
$$ \frac{\mathrm{d} \mathcal{J}}{\mathrm{d} \theta}=\frac{\partial \mathcal{J}}{\partial \theta}+\frac{\partial \mathcal{J}}{\partial w^\star} \frac{\partial w^\star}{\partial \theta} $$
其中\( \frac{\partial \mathcal{J}}{\partial \theta}\)和\( \frac{\partial \mathcal{J}}{\partial w^\star} \)都是可以直接利用Pytorch或者Tensorflow中的API直接计算得到,但是后一项\( \frac{\partial w^\star}{\partial \theta} \)是无法直接计算得到的,也是本文的主要贡献。
基于Cauchy隐性函数定理可以得到:如果对于一些 使得低层次优化问题有解,也就是 \( \left.\frac{\partial \mathcal{E}}{\partial w}\right|_{\left(w^{\prime}, \theta^{\prime}\right)}=0\)和\(\left(\frac{\partial^2 \mathcal{E}}{\partial w \partial w^{\top}}\right)^{-1} \)是可逆的,那么存在一个函数\(w^\star=w^\star(\theta)\)在\( \left(w^{\prime}, \theta^{\prime}\right) \text { s.t. }\left.\frac{\partial \mathcal{E}}{\partial w}\right|_{\left(w^\star\left(\theta^{\prime}\right), \theta^{\prime}\right)}=0\),我们有
$$ \left.\frac{\partial w^\star}{\partial \theta}\right|_{\theta^{\prime}}=-\left.\left[\frac{\partial^2 \mathcal{E}}{\partial w \partial w^{\top}}\right]^{-1} \cdot \frac{\partial^2 \mathcal{E}}{\partial w \partial \theta^{\top}}\right|_{\left(w^\star\left(\theta^{\prime}\right), \theta^{\prime}\right)} $$
因此,该问题可以被求解为
$$ \frac{\mathrm{d} \mathcal{J}}{\mathrm{d} \theta}=\frac{\partial \mathcal{J}}{\partial \theta}-\left.\frac{\partial \mathcal{J}}{\partial w^\star} \cdot\left(\frac{\partial^2 \mathcal{E}}{\partial w \partial w^{\top}}\right)^{-1} \cdot \frac{\partial^2 \mathcal{E}}{\partial w \partial \theta^{\top}}\right|_{\left(w^\star(\theta), \theta\right)} $$
然而,对于神经网络的参数来说,计算Hessian矩阵的逆值是难以实现的。为了应对这一挑战,我们可以首先计算\( z^\star \triangleq \frac{\partial \mathcal{J}}{\partial w^\star} \cdot\left(\frac{\partial^2 \mathcal{E}}{\partial w \partial w^{\top}}\right)^{-1}\),这也被称为反向量-黑森积。求解\( z^\star \)可以通过求解下面的线性方程:
$$ g_w(z)=\frac{\partial}{\partial w}\left(\frac{\partial \mathcal{E}}{\partial w^{\top}} \cdot z\right)-\left.\frac{\partial \mathcal{J}}{\partial w}\right|_{w=w^\star}=0 $$
我们只需要以较低的计算成本计算两个Jacobian向量乘积,这不需要创建一个巨大的Hessian矩阵实例。具体来说,我们使用低秩的Broyden方法来迭代近似解:
首先,近似将\( \left(\frac{\partial^2 \mathcal{E}}{\partial w \partial w^{\top}}\right)^{-1} \)表示为:
$$ \left(\frac{\partial^2 \mathcal{E}}{\partial w \partial w^{\top}}\right)^{-1} \approx B_i=-I+\sum_{k=1}^i u_k v_k^{\top} $$
随后更新参数
$$ \begin{aligned} z_{i+1} &=z_i-\alpha \cdot B_i g_i(z) \\ u_{i+1} &=\frac{\Delta z_{i+1}-B_i \Delta g_{i+1}}{\left(\Delta z_{i+1}\right)^{\top} B_i \Delta g_{i+1}} \\ v_{i+1} &=B_i \Delta z_{i+1} \end{aligned} $$
其中\( \Delta z_{i+1}=z_{i+1}-z_i, \Delta g_{i+1}=g_{i+1}-g_i\),\( \alpha\)是学习率。
因此,逆Hessian矩阵可以通过以下方式更新
$$ \left(\frac{\partial^2 \mathcal{E}}{\partial w \partial w^{\top}}\right)^{-1} \approx B_{i+1}=B_i+\frac{\Delta z_{i+1}-B_i \Delta g_{i+1}}{\left(\Delta z_{i+1}\right)^{\top} B_i \Delta g_{i+1}} \Delta z_{i+1}^{\top} B_i $$
最后,通过m次迭代得到的解\(z_m\)就可以使用去计算梯度\( \frac{\mathrm{d} \mathcal{J}}{\mathrm{d} \theta} \),这样就完成了外层优化过程。
作者随后还给出了一个理论分析,也就是说内层优化过程是收敛的,也就是说,
$$ \left\| w_t-w \right\| _2\leqslant p_t\left\| w \right\| _2 $$
其中\(p_t<1\),\( p_t\rightarrow 0,t\rightarrow \infty \)。
定理:如果一些假设成立且关于\(z\)线性方程可以用Broyden方法求解,那么存在一个常数\( M>0 \),使以下不等式成立:
$$ \left\|\mathrm{d}_2 J_t-\mathrm{d}_2 J\right\|_2 \leqslant\left(L\left(1+\kappa+\frac{\rho M}{\mu^2}\right)+\frac{\tau M}{\mu}\right) p_t\|w\|_2+M \kappa\left(1-\frac{1}{m \kappa}\right)^{\frac{m^2}{2}} . $$
其中, \(\mathrm{d}_2 J_t \)和\(\mathrm{d}_2 J\)分别是计算出的和真实的关于\(\theta\)的超阶梯。
实验结果
这篇文章主要和hPINN、PINN-LS、PI-DeepONet、Truncated Unrolled Differentiation(TRMD)和Neumann Series (Neumann)这几种方法进行比较,主要在在泊松方程、热方程、伯格斯方程和纳维亚-斯托克斯方程上面进行了实验,具体效果如下:
$$ \scriptsize \begin{array}{c|cccccc} \hline \text { Objective }(\mathcal{J}) & \text { Poisson's 2d CG } & \text { Heat 2d } & \text { Burgers 1d } & \text { NS Shape } & \text { NS 2inlets } & \text { NS backstep } \\ \hline \text { Initial guess } & 0.400 & 0.142 & 0.0974 & 1.78 & 0.0830 & 0.138 \\ \text { hPINN-P } & 0.373 & 0.132 & 0.0941 & - & 0.0732 & 0.0586 \\ \text { hPINN-A } & 0.352 & 0.138 & 0.0895 & - & 0.0867 & 0.0696 \\ \text { PINN-LS } & 0.239 & 0.112 & 0.0702 & - & 0.0634 & 0.0831 \\ \text { PI-DeepONet } & 0.392 & 0.0501 & 0.0710 & \mathbf{1 . 2 7} & 0.0850 & 0.0670 \\ \hline \text { Ours } & \mathbf{0 . 1 6 0} & \mathbf{0 . 0 3 7 9} & \mathbf{0 . 0 6 6 2} & \mathbf{1 . 2 7} & \mathbf{0 . 0 3 6 9} & \mathbf{0 . 0 3 6 5} \\ \text { Reference values } & 0.159 & 0.0378 & 0.0634 & 1.27 & 0.0392 & 0.0382 \\ \hline \end{array}\\ \begin{array}{c|cccccc} \hline \text { Objective }(\mathcal{J}) & \text { Poisson's 2d CG } & \text { Heat 2d } & \text { Burgers 1d } & \text { NS Shape } & \text { NS 2inlets } & \text { NS backstep } \\ \hline \text { Initial guess } & 0.400 & 0.142 & 0.0974 & 1.77 & 0.0830 & 0.138 \\ \text { TRMD } & 0.224 & 0.0735 & 0.0671 & - & 0.0985 & 0.0391 \\ T 1-T 2 & 0.425 & 0.0392 & 0.0865 & 1.68 & 0.115 & 0.0879 \\ \text { Neumann } & 0.225 & 0.0782 & 0.0703 & 1.31 & 0.0962 & 0.0522 \\ \hline \text { Broyden(Ours) } & \mathbf{0 . 1 6 0} & \mathbf{0 . 0 3 7 9} & \mathbf{0 . 0 6 6 2} & \mathbf{1 . 2 7} & \mathbf{0 . 0 3 6 9} & \mathbf{0 . 0 3 6 5} \\ \hline \end{array} $$
总结
本文介绍的这篇文章算是偏微分方程约束的最优化问题的SOTA结果,作者引入了双层优化的方法,避免了loss相加导致的学习失败的情形,是一篇非常好的文章。未来的研究方向可以是引入效果更好的优化方法、算子学习理论的优化以及生成控制输入的网络结构设计,这些都属于尚未探索的领域,相信这些会为Physics Informed Machine Learning带来全新的视角。