时间序列数据处理1——基于Pytorch构建长短时记忆网络（LSTM）

 本文主要实现基于pytorch构建长短时记忆网络（LSTM）的相关搬运工作。

1. LSTM简介

1.1 从RNN说起

循环神经网络（Recurrent Neural Network，RNN）是一种用于处理序列数据的神经网络。相比一般的神经网络来说，他能够处理序列变化的数据。

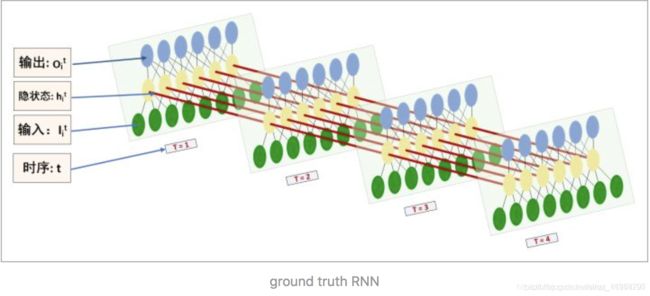
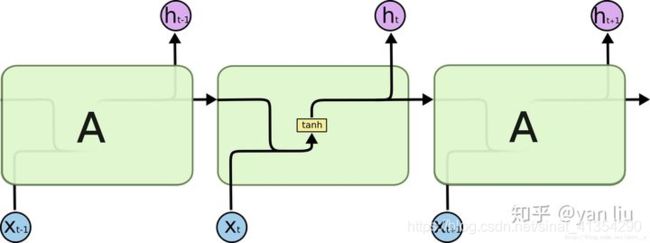
RNN之所以在时序数据上有着优异的表现是因为RNN在 $t$ 时间片时会将 $t-1$ 时间片的隐节点作为当前时间片的输入，也就是RNN具有图1的结构。这样有效的原因是之前时间片的信息也用于计算当前时间片的内容，而传统模型的隐节点的输出只取决于当前时间片的输入特征。


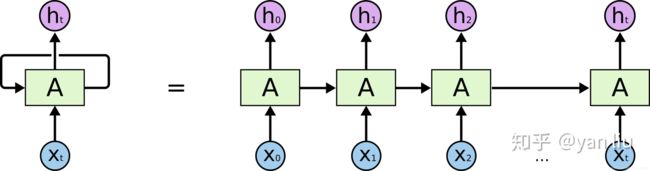
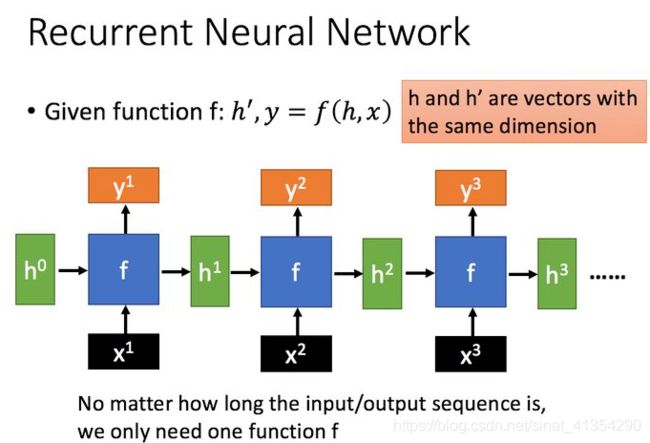
$x$ 为当前状态下数据的输入，$h$ 表示接收到的上一个节点的输入。

$y$ 为当前节点状态下的输出，而 $h{}^{\prime }$ 为传递到下一个节点的输出。

通过序列形式的输入，我们能够得到如下形式的RNN：

梯度消失/爆炸

梯度消失和梯度爆炸是困扰RNN模型训练的关键原因之一，产生梯度消失和梯度爆炸是由于RNN的权值矩阵循环相乘导致的，相同函数的多次组合会导致极端的非线性行为。梯度消失和梯度爆炸主要存在RNN中，因为RNN中每个时间片使用相同的权值矩阵。对于一个DNN，虽然也涉及多个矩阵的相乘，但是通过精心设计权值的比例可以避免梯度消失和梯度爆炸的问题 [2]。

1.2 什么是LSTM

长短期记忆（Long short-term memory, LSTM）是一种特殊的RNN，主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说，就是相比普通的RNN，LSTM能够在更长的序列中有更好的表现。

Understanding LSTM Networks

LSTM结构（图右）和普通RNN的主要输入输出区别如下所示：

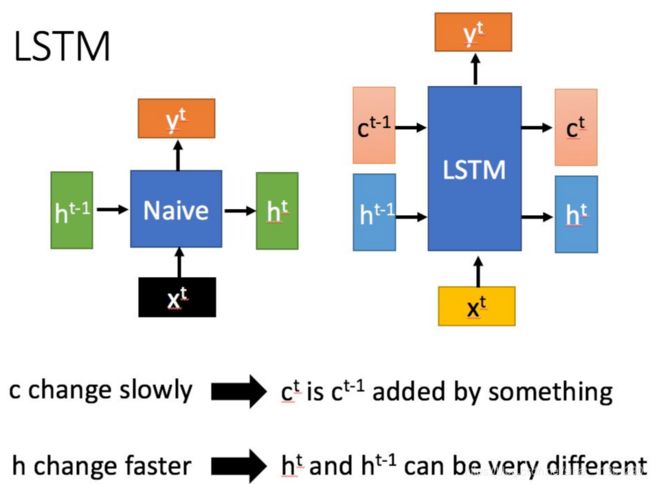
相比RNN只有一个传递状态 $h^t$ ，LSTM有两个传输状态，一个 $c^t$（cell state），和一个 $h^t$（hidden state）。（Tips：RNN中的 $h^t$对于LSTM中的$c^t$）

LSTM提出的动机是为了解决上面我们提到的长期依赖问题。传统的RNN节点输出仅由权值，偏置以及激活函数决定（图3）。RNN是一个链式结构，每个时间片使用的是相同的参数。

而LSTM之所以能够解决RNN的长期依赖问题，是因为LSTM引入了门（gate）机制用于控制特征的流通和损失。LSTM是由一系列LSTM单元（LSTM Unit）组成，其链式结构如下图。

在后面的章节中我们再对LSTM的详细结构进行讲解，首先我们先弄明白LSTM单元中的每个符号的含义。每个黄色方框表示一个神经网络层，由权值，偏置以及激活函数组成；每个粉色圆圈表示元素级别操作；箭头表示向量流向；相交的箭头表示向量的拼接；分叉的箭头表示向量的复制。总结如图5.

1.3 深入LSTM

首先使用LSTM的当前输入 $x^t$ 和上一个状态传递下来的 $h^{t-1}$ 拼接训练得到四个状态:$$z=tanh(w\cdot [x^t,h^{t-1}])$$$$z^i=\sigma (w^i\cdot [x^t,h^{t-1}])$$$$z^f=\sigma (w^f\cdot [x^t,h^{t-1}])$$$$z^o=\sigma (w^o\cdot [x^t,h^{t-1}])$$
其中，$z^i$，$z^f$，$z^o$ 是由拼接向量乘以权重矩阵之后，再通过一个 $sigmoid$ 激活函数转换成0到1之间的数值，来作为一种门控状态。而$z$则是将结果通过一个$tanh$激活函数将转换成-1到1之间的值（这里使用$tanh$是因为这里是将其做为输入数据，而不是门控信号）。

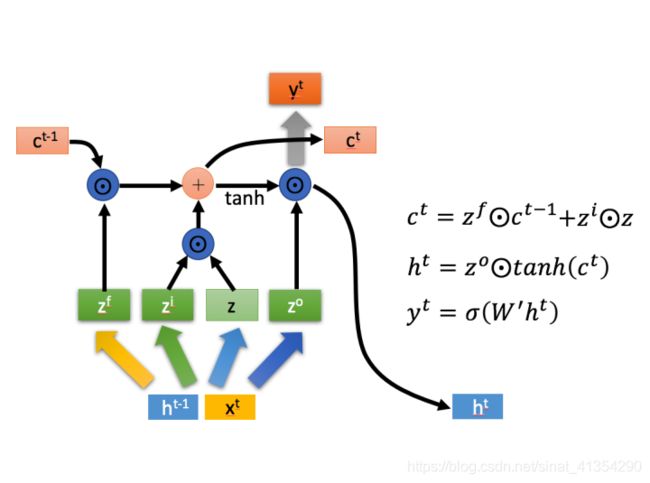
$\odot$是Hadamard Product，也就是操作矩阵中对应的元素相乘，因此要求两个相乘矩阵是同型的。 $\oplus$则代表进行矩阵加法。
LSTM内部主要有三个阶段：

1. 忘记阶段。这个阶段主要是对上一个节点传进来的输入进行选择性忘记。简单来说就是会 “忘记不重要的，记住重要的”。

   具体来说是通过计算得到的 $z^f$（f表示forget）来作为忘记门控，来控制上一个状态的 $c^{t-1}$哪些需要留哪些需要忘。

2. 选择记忆阶段。这个阶段将这个阶段的输入有选择性地进行“记忆”。主要是会对输入$x^t$进行选择记忆。哪些重要则着重记录下来，哪些不重要，则少记一些。当前的输入内容由前面计算得到的 $z$表示。而选择的门控信号则是由$z^i$（i代表information）来进行控制。

   将上面两步得到的结果相加，即可得到传输给下一个状态的$c^t$。也就是上图中的第一个公式。

3. 输出阶段。这个阶段将决定哪些将会被当成当前状态的输出。主要是通过$z^o$来进行控制的。并且还对上一阶段得到的 $c^o$进行了放缩（通过一个tanh激活函数进行变化）。

   与普通RNN类似，输出$y^t$往往最终也是通过 $h^t$变化得到。

LSTM的核心部分是在图4中最上边类似于传送带的部分（图6），这一部分一般叫做单元状态（cell state）它自始至终存在于LSTM的整个链式系统中。
整体流程是：遗忘→根据现有的输入和上一个cell的输出更新状态→根据现有的状态输出预测值。

图中
$$C_t=f_t\times C_{t-1}+i_t\times \widetilde{C_t}$$

LSTM第一部分：遗忘

$f_t$为遗忘门，$f_t$是一个向量，向量的每个元素位于$[0,1]$范围内，通常使用$sigmoid$作为激活函数。

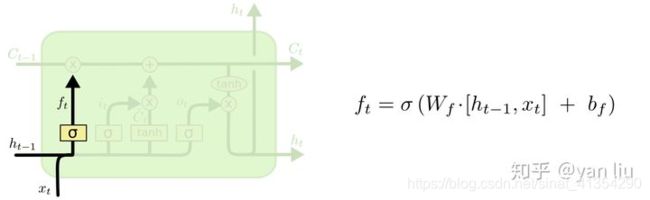
LSTM第二部分：添加信息到现有状态矩阵中

$\widetilde{C_t}$表示单元状态更新值，由输入数据$x_t$和隐节点$h_{t-1}$ 经由一个神经网络层得到，单元状态更新值的激活函数通常使用$tanh$ 。

$i_t$用于控制$\widetilde{C_t}$的哪些特征用于更新$C_t$.


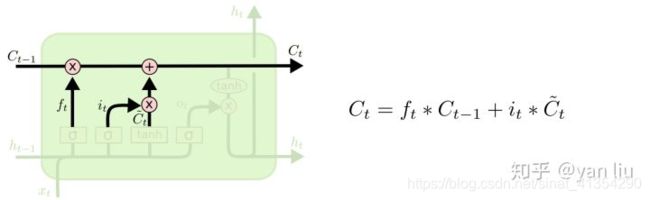
LSTM第三部分：决定输出

最后，为了计算预测值 $\widehat{y_t}$和生成下个时间片完整的输入，我们需要计算隐节点的输出$h_t$。

在[3]的论文中指出，通过将 $b_o$的均值初始化为$1$ ，可以使LSTM达到同GRU近似的效果。

其他LSTM：

1. GRU，LSTM是表现最好的模型；
2. GRU的在除了语言模型的场景中表现均超过LSTM；
3. LSTM的输出门的偏置的均值初始化为1时，LSTM的性能接近GRU；
4. 在LSTM中，门的重要性排序是遗忘门 > 输入门 > 输出门。

1.4 总结

以上，就是LSTM的内部结构。通过门控状态来控制传输状态，记住需要长时间记忆的，忘记不重要的信息；而不像普通的RNN那样只能够“呆萌”地仅有一种记忆叠加方式。对很多需要“长期记忆”的任务来说，尤其好用。
但也因为引入了很多内容，导致参数变多，也使得训练难度加大了很多。因此很多时候我们往往会使用效果和LSTM相当但参数更少的GRU来构建大训练量的模型。
详细信息见参考资料1、2.

2. 基于Pytorch的实战

2.1 核心API

torch.nn.LSTM(*args,**kwargs)
#其构造器的参数列表如下：
#input_size – 每个time step中其输入向量x_t的维度。
#hidden_size – 每个time step中其隐藏状态向量h_t的维度。
#num_layers – 每个time step中其纵向有几个LSTM单元，默认为1。
#如果取2，第二层的x_t是第一层的h_t，有时也会加一个dropout因子。
#bias – 如果为False，则计算中不用偏置，默认为True。
#batch_first –若为True，则实际调用时input和output张量格式为(batch, seq, feature)，
#默认为False。
#dropout – 是否加dropout，Default: 0。
#bidirectional – 是否为双向LSTM，Default: False。

模型定义：

rnn = nn.LSTM(10, 20, 2)  #(input_size,hidden_size,num_layers)
input_size – The number of expected features in the input x.
			 白话： 就是你输入x的向量大小（x向量里有多少个元素）
			 每一个输入x的维度，mnist中就是1×28，也就是1行
hidden_size – The number of features in the hidden state h 。
		     白话：就是LSTM在运行时里面的维度。隐藏层状态的维数，即隐藏层节点的个数，
		     这个和单层感知器的结构是类似的。这个维数值是自定义的。
		     隐层的大小，这个参数就是比如我们输入是1×28的矩阵大小，隐藏为128,
		     就是将输入维度变为1×128,当然lstm输入也是1×128
num_layers – Number of recurrent layers. 
		   	 LSTM 堆叠的层数，默认值是1层，
			 如果设置为2，第二个LSTM接收第一个LSTM的计算结果。
			 
# Inputs: input, (h_0, c_0) 
# Outputs: output, (h_n, c_n)
Outputs=lstm(Inputs)


1）h_0, c_0分别代表batch中每个元素的hidden state和cell state的初始化值。
输入数据格式：
	input(seq_len, batch, input_size)
	h0(num_layers * num_directions, batch, hidden_size)
	c0(num_layers * num_directions, batch, hidden_size)
	
input(seq_len, batch, input_size)	
第一维体现的是序列（sequence）结构,也就是序列的个数，
时间步数，就是图片中绿色框的个数，图中用A表示。
对于mnist来说，总共有28个，28行，28×28。
用文章来说，就是每个句子的长度，因为是喂给网络模型，一般都设定为确定的长度，
也就是我们喂给LSTM神经元的每个句子的长度，
当然，如果是其他的带有带有序列形式的数据，则表示一个明确分割单位长度。
例如是如果是股票数据内，
这表示特定时间单位内，有多少条数据。
这个参数也就是明确这个层中有多少个确定的单元来处理输入的数据。

第二维度体现的是batch_size，也就是一次性喂给网络多少条句子，
或者股票数据中的，一次性喂给模型多少是个时间单位的数据，具体到每个时刻，
也就是一次性喂给特定时刻处理的单元的单词数或者该时刻应该喂给的股票数据的条数。

第三位体现的是输入的元素（elements of input），
也就是，每个具体的单词用多少维向量来表示，
或者股票数据中 每一个具体的时刻的采集多少具体的值，
比如最低价，最高价，均价，5日均价，10均价，等等

2）h_n, c_n分别代表当t = seq_len时，hidden state和cell state的值。
输出数据格式：
	output(seq_len, batch, hidden_size * num_directions)
	hn(num_layers * num_directions, batch, hidden_size)
	cn(num_layers * num_directions, batch, hidden_size)

Outputs:output,(h_n,c_n):
 1. output保存了最后一层，每个time step的输出h.
 2. h_n保存了每一层，最后一个time step的输出h.
 3. c_n与h_n一致，只是它保存的是c的值。

3）如果batch_first=False时，
	input格式为：(seq_len, batch=1, input_size)，
	output格式为：(seq_len, batch=1, num_directions * hidden_size)。
   但是当batch_first=True时，
	input的格式变为：(batch_size, seq_len, input_size)，
	而output的格式变为：(batch_size, seq_len, num_directions * hidden_size)。

单层感知器的结构：

2.2 LSTM简单测试

单向LSTM的使用：

rnn = nn.LSTM(input_size=10, hidden_size=20, num_layers=2)
# (input_size,hidden_size,num_layers)
# 输入数据x的向量维数10, 设定lstm隐藏层的特征维度20, 此model用2个lstm层，两层神经元。
# 记住就是神经元，这个时候神经层的详细结构还没确定，
# 仅仅是说这个网络可以接受[seq_len,batch_size,10]的数据输入
print(rnn.all_weights)

input = torch.randn(5, 3, 10)#(seq_len, batch, input_size)
# 输入的input为，
# 序列长度seq_len=5, 每次取的minibatch大小，batch_size=3, 
# 数据向量维数=10（仍然为x的维度）。
# 每次运行时取3个含有5个字的句子（且句子中每个字的维度为10进行运行）

# 手动初始化，如果不初始化，PyTorch默认初始化为全零的张量。
h0 = torch.randn(2, 3, 20) #(num_layers,batch,output_size)
c0 = torch.randn(2, 3, 20) #(num_layers,batch,output_size)
# 初始化的隐藏元和记忆元,通常它们的维度是一样的
# 2个LSTM层，batch_size=3, 隐藏层的特征维度20

output, (hn, cn) = rnn(input, (h0, c0))
# 这里有2层lstm，
# output是最后一层lstm的每个词向量对应隐藏层的输出,其与层数无关，只与序列长度相关

# hn,cn是所有层最后一个隐藏元和记忆元的输出
output.shape #(seq_len, batch, output_size)
#torch.Size([5, 3, 20])
hn.shape #(num_layers, batch, output_size)
#torch.Size([2, 3, 20])
cn.shape #(num_layers, batch, output_size)
#torch.Size([2, 3, 20])

理解：

• output：对于每一个step，相当于也就是seq_len中的每一步，都有一个output_size维度的特征输出，所以output的维度是5，3，20(seq_len, batch, output_size).
• hc其实是最后一个时间节点t的隐藏层的特征，因为lstm中设置了num_layers=2,所以每一层lstm最后一个时间节点都会有一个output_size维度特征的输出，所以他的输出维度为2, 3, 20(num_layers, batch, output_size)
• cn与hc相同

详细信息见参考资料4、5、6、7、8.

2.3 实现MNIST手写数字分类

1. 导入库

   import torch
   from torch import nn
   import torchvision.datasets
   import torchvision.transforms as transforms
   import matplotlib.pyplot as plt
   import warnings
   warnings.filterwarnings('ignore')
   torch.manual_seed(1)    # reproducible
   

2. 定义超参数
   input_x就是图片中输入X的序列，相当于每一个输入X，都是1×28的大小，time_steps就是图片中绿色框的个数，图中用A表示的，也就是说总共有28个，因为图像是28×28。

   # Hyper Parameters
   EPOCH = 1# 训练整批数据多少次, 为了节约时间, 我们只训练一次
   BATCH_SIZE = 64
   TIME_STEP = 28# rnn 时间步数 / 图片高度 (因为每张图像为28×28,而每一个序列长度为1×28,所以总共28个1×28,)
   INPUT_SIZE = 28# rnn 每步输入值 / 图片每行像素（输入序列的长度，因为是28×28的大小，所以每一个序列我们设置长度为28，每一个输入都是28个像素点）
   LR = 0.01# learning rate
   DOWNLOAD_MNIST = True# 如果你已经下载好了mnist数据就写上 Fasle
   
   NUM_CLASSES = 10 #输入为10,因为共10类
   HIDDEN_SIZE = 128 #隐层的大小，这个参数就是比如我们输入是1×28的矩阵大小，隐藏为128,就是将输入维度变为1×128,当然lstm输入也是1×128
   

3. 训练和测试数据定义

   # Mnist 手写数字
   train_data = torchvision.datasets.MNIST(
       root='./mnist/',    # 保存或者提取位置
       train=True,  # this is training data
       transform=torchvision.transforms.ToTensor(),    # 转换 PIL.Image or numpy.ndarray 成
                                                       # torch.FloatTensor (C x H x W), 训练的时候 normalize 成 [0.0, 1.0] 区间
       download=DOWNLOAD_MNIST,          # 没下载就下载, 下载了就不用再下了
   )
   
   # plot one example
   print(train_data.train_data.size())     # (60000, 28, 28)
   print(train_data.train_labels.size())   # (60000)
   plt.imshow(train_data.train_data[0].numpy(), cmap='gray')
   plt.title('MNIST:%i' % train_data.train_labels[0])
   plt.show()
   

   

4. 读取数据dataload

   # Data Loader for easy mini-batch return in training
   train_loader = torch.utils.data.DataLoader(
       dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
   
   data = next(iter(train_loader))
   print(data[0].shape)  # torch.Size([64, 1, 28, 28])
   print(data[1].shape)  # torch.Size([64])
   
   
   for step, (b_x, b_y) in enumerate(train_loader):        # gives batch data
       # reshape x to (batch, time_step, input_size) => torch.Size([64, 28, 28])
       b_x = b_x.view(-1, 28, 28)
       print(b_x.shape)  # torch.Size([64, 28, 28])
       print(b_y.shape)  # torch.Size([64])
   
       print(b_x[0].shape)  # torch.Size([28, 28])
       print(b_y[0])  # tensor(9)
       break
   
   test_data = torchvision.datasets.MNIST(
       root='./mnist/', train=False, transform=transforms.ToTensor())
   test_x = test_data.test_data.type(torch.FloatTensor)[
       :2000]/255.   # shape (2000, 28, 28) value in range(0,1)
   test_y = test_data.test_labels.numpy()[:2000]    # covert to numpy array
   print(test_x.shape)  # torch.Size([2000, 28, 28])
   

   python中view()函数使用：
   view()的作用相当于numpy中的reshape，重新定义矩阵的形状。
   view中一个参数定为-1，代表动态调整这个维度上的元素个数，以保证元素的总数不变。

   A = torch.arange(0, 16)
   print(A.shape)
   B = A.view(-1,2)
   print(B.shape)
   C = A.view(-1,2,2)
   print(C.shape)
   

   

5. 定义模型

   class RNN(nn.Module):
       def __init__(self):
           super(RNN, self).__init__()
   
           self.rnn = nn.LSTM(     # LSTM 效果要比 nn.RNN() 好多了
               input_size=INPUT_SIZE,      # 图片每行的数据像素点
               hidden_size=HIDDEN_SIZE,     # rnn hidden unit
               num_layers=1,       # 有几层 RNN layers
               batch_first=True,   # input & output 会是以 batch size 为第一维度的特征集 e.g. (batch, time_step, input_size)
           )
   
           self.out = nn.Linear(HIDDEN_SIZE, NUM_CLASSES)    # 输出层
   
       def forward(self, x):
           # x shape (batch, time_step, input_size)
           # r_out shape (batch, time_step, output_size)
           # h_n shape (n_layers, batch, hidden_size)   LSTM 有两个 hidden states, h_n 是分线, h_c 是主线
           # h_c shape (n_layers, batch, hidden_size)
           r_out, (h_n, h_c) = self.rnn(x, None)   # None 表示 hidden state 会用全0的 state
                   
           # 这个地方选择lstm_output[-1]，也就是相当于最后一个输出，因为其实每一个cell（相当于图中的A）都会有输出，但是我们只关心最后一个
           # 选取最后一个时间点的 r_out 输出 r_out[:, -1, :] 的值，也是 h_n 的值
           # torch.Size([64, 28, 128])->torch.Size([64,128])
           out = self.out(r_out[:, -1, :]) # torch.Size([64, 128])-> torch.Size([64, 10])
           return out
   
   rnn = RNN()
   print(rnn)
   

   

6. 模型训练和预测
   我们将图片数据看成一个时间上的连续数据, 每一行的像素点都是这个时刻的输入, 读完整张图片就是从上而下的读完了每行的像素点. 然后我们就可以拿出 RNN 在最后一步的分析值判断图片是哪一类了

   optimizer = torch.optim.Adam(rnn.parameters(), lr=LR)   # optimize all cnn parameters
   loss_func = nn.CrossEntropyLoss()                       # the target label is not one-hotted
   
   # training and testing
   for epoch in range(EPOCH):
       for step, (b_x, b_y) in enumerate(train_loader):        # gives batch data
           b_x = b_x.view(-1, 28, 28)                      # reshape x to (batch, time_step, input_size) => torch.Size([64, 28, 28])
           
           output = rnn(b_x)                               # rnn output
           loss = loss_func(output, b_y)                   # cross entropy loss
           optimizer.zero_grad()                           # clear gradients for this training step
           loss.backward()                                 # backpropagation, compute gradients
           optimizer.step()                                # apply gradients
   
           if step % 50 == 0:
               test_output = rnn(test_x)                   # (samples, time_step, input_size)
               pred_y = torch.max(test_output, 1)[1].data.numpy()
               accuracy = float((pred_y == test_y).astype(int).sum()) / float(test_y.size)
               print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % accuracy)
   

   最后我们再来取10个数据, 看看预测的值到底对不对:

   # print 10 predictions from test data
   test_output = rnn(test_x[:10].view(-1, 28, 28))
   pred_y = torch.max(test_output, 1)[1].data.numpy()
   print(pred_y, 'prediction number')
   print(test_y[:10], 'real number')
   

   
   详细信息见参考资料9.

详细信息见参考资料1.

参考资料

1. 人人都能看懂的LSTM
2. 详解LSTM
3. 神经网络学习小记录3——利用tensorflow构建长短时记忆网络（LSTM）
4. LSTM原理及实战
5. 聊一聊PyTorch中LSTM的输出格式
6. PyTorch 中的 LSTM模型参数解释
7. LSTM神经网络输入输出究竟是怎样的？
8. 用「动图」和「举例子」讲讲 RNN
9. LSTM原理以及基于PyTorch的LSTM实现MNIST手写数字