数据探索(数据集成、数据变换、数据规约)③—Python对数据规范化、数据离散化、属性构造、主成分分析 降维
Python介绍、 Unix & Linux & Window & Mac 平台安装更新 Python3 及VSCode下Python环境配置配置
python基础知识及数据分析工具安装及简单使用(Numpy/Scipy/Matplotlib/Pandas/StatsModels/Scikit-Learn/Keras/Gensim))
数据探索(数据清洗)①——数据质量分析(对数据中的缺失值、异常值和一致性进行分析)
数据探索(数据清洗)②—Python对数据中的缺失值、异常值和一致性进行处理
数据探索(数据集成、数据变换、数据规约)③—Python对数据规范化、数据离散化、属性构造、主成分分析 降维
数据探索(数据特征分析)④—Python分布分析、对比分析、统计量分析、期性分析、贡献度分析、相关性分析
挖掘建模①—分类与预测
挖掘建模②—Python实现预测
挖掘建模③—聚类分析(包括相关性分析、雷达图等)及python实现
挖掘建模④—关联规则及Apriori算法案例与python实现
挖掘建模⑤—因子分析与python实现
数据探索(数据集成、数据变换、数据规约)③—Python对数据规范化、数据离散化、属性构造、主成分分析 降维
- 数据集成
-
- 实体识别
- 冗余属性识别
- 数据变换
-
- 规范化
-
- 最小-最大规范化
-
- Python处理
- 零-均值规范化
-
- Python处理
- 小数定标规范化
-
- Python处理
- 连续属性离散化
- 属性构造
- 小波变换
- 数据规约
-
- 属性规约
-
- 合并属性
- 逐步向前选择
- 逐步向后删除
- 决策树规约
- 主成分分析
-
- Python实现
-
- 1)n_components
- 2) copy:
- 3)whiten
- 数值规约
数据集成
-
数据挖掘需要的数据往往分布在不同的数据源中,数据集成就是将多个数据源合并存放在一个一致的数据存储(如数据仓库)中的过程。
-
在数据集成时,来自多个数据源的现实世界实体的表达形式是不一样的,不一定是匹配的,要考虑实体识别问题和属性冗余问题,从而把源数据在最低层上加以转换、提炼和集成。
实体识别
实体识别的任务是检测和解决同名异义、异名同义、单位不统一的冲突。
- 同名异义:数据源A中的属性ID和数据源B中的属性ID分别描述的是菜品编号和订单编号,即描述的是不同的实体。
- 异名同义:数据源A中的sales_dt和数据源B中的sales_date都是是描述销售日期的,即A. sales_dt= B. sales_date。
- 单位不统一:描述同一个实体分别用的是国际单位和中国传统的计量单位。
冗余属性识别
- 数据集成往往导致数据冗余
- 同一属性多次出现
- 同一属性命名不一致导致重复
- 不同源数据的仔细整合能减少甚至避免数据冗余与不一致,以提高数据挖掘的速度和质量。对于冗余属性要先分析检测到后再将其删除。
- 有些冗余属性可以用相关分析检测到。给定两个数值型的属性A和B,根据其属性值,可以用相关系数度量一个属性在多大程度上蕴含另一个属性。
数据变换
主要是对数据进行规范化的操作,将数据转换成“适当的”格式,以适用于挖掘任务及算法的需要。
简单函数变换就是对原始数据进行某些数学函数变换,常用的函数变换包括平方、开方、对数、差分运算等,即:

规范化
数据标准化(归一化)处理是数据挖掘的一项基础工作,不同评价指标往往具有不同的量纲和量纲单位,数值间的差别可能很大,不进行处理可能会影响到数据分析的结果,为了消除指标之间的量纲和大小不一的影响,需要进行数据标准化处理,将数据按照比例进行缩放,使之落入一个特定的区域,从而进行综合分析。如将工资收入属性值映射到[-1,1]或者[0,1]之间。
下面介绍三种规范化方法:最小-最大规范化、零-均值规范化、小数定标规范化
最小-最大规范化
也称为离差标准化,是对原始数据的线性变换,使结果值映射到[0,1]之间。转换函数如:

其中max为样本数据的最大值, min为样本数据的最小值。max-min 为极差。
Python处理
import numpy as np
(data - data.min())/(data.max() - data.min())
零-均值规范化
也叫标准差标准化,经过处理的数据的平均数为0,标准差为1。转化函数为:

Python处理
(data - data.mean())/data.std()
小数定标规范化
通过移动属性值的小数位数,将属性值映射到[-1,1]之间,移动的小数位数取决于属性值绝对值的最大值。转化函数为:

Python处理
data/10**np.ceil(np.log10(data.abs().max()))
连续属性离散化
一些数据挖掘算法,特别是某些分类算法,要求数据是分类属性形式,如ID3算法、Apriori算法等。这样,常常需要将连续属性变换成分类属性,即连续属性离散化。
-
离散化的过程
连续属性变换成分类属性涉及两个子任务:决定需要多少个分类变量,以及确定如何将连续属性值映射到这些分类值。 -
常用的离散化方法
常用的无监督离散化方法有:等宽法、等频法、基于聚类分析的方法
属性构造
在数据挖掘的过程中,为了帮助提取更有用的信息、挖掘更深层次的模式,提高挖掘结果的精度,需要利用已有的属性集构造出新的属性,并加入到现有的属性集合中。
比如已有人的身高体重,构造一个关键指标——体重指数BMI,改过程就是构造属性:
BMI=(体重)/身高²
身高与体重的比例生成的BMI指数,能用来衡量人的体形发育匀称度和体型,作为评定人的身体匀称度。
小波变换
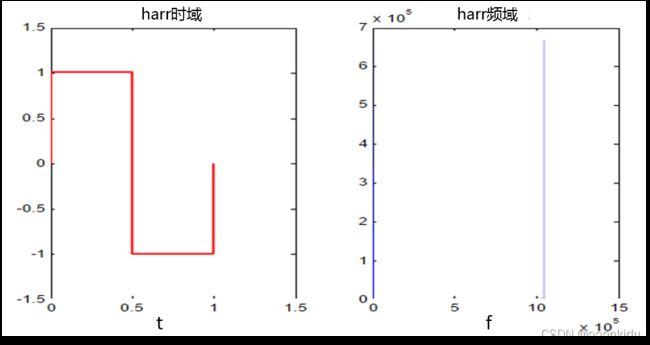
小波基函数是一种具有局部支集的函数,平均值为0,小波基函数满足: 。Haar小波基函数是常用的小波基函数,如下图所示:
。Haar小波基函数是常用的小波基函数,如下图所示:


数据规约
- 数据规约是将海量数据进行规约,规约之后的数据仍接近于保持原数据的完整性,但数据量小得多。
- 通过 数据规约,可以达到:
1.降低无效、错误数据对建模的影响,提高建模的准确性
2.少量且具代表性的数据将大幅缩减数据挖掘所需的时间
3.降低储存数据的成本
属性规约
属性规约常用方法有:合并属性、逐步向前选择、逐步向后删除、决策树归纳、主成分分析
合并属性
逐步向前选择
逐步向后删除
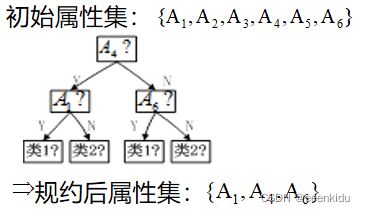
决策树规约
主成分分析
Python实现
from sklearn.decomposition import PCA
PCA(n_components=None, *, copy=True, whiten=False, svd_solver=“auto”, tol=0.0, iterated_power=“auto”, random_state=None)
1)n_components
这个参数可以帮我们指定希望PCA降维后的特征维度数目。最常用的做法是直接指定降维到的维度数目,此时n_components是一个大于等于1的整数。当然,我们也可以指定主成分的方差和所占的最小比例阈值,让PCA类自己去根据样本特征方差来决定降维到的维度数,此时n_components是一个(0,1]之间的数。当然,我们还可以将参数设置为"mle", 此时PCA类会用MLE算法根据特征的方差分布情况自己去选择一定数量的主成分特征来降维。我们也可以用默认值,即不输入n_components,此时n_components=min(样本数,特征数)。
2) copy:
类型:bool,True或者False,缺省时默认为True。
意义:表示是否在运行算法时,将原始训练数据复制一份。若为True,则运行PCA算法后,原始训练数据的值不会有任何改变,因为是在原始数据的副本上进行运算;若为False,则运行PCA算法后,原始训练数据的值会改,因为是在原始数据上进行降维计算。
3)whiten
判断是否进行白化。所谓白化,就是对降维后的数据的每个特征进行归一化,让方差都为1.对于PCA降维本身来说,一般不需要白化。如果你PCA降维后有后续的数据处理动作,可以考虑白化。默认值是False,即不进行白化。
除了这些输入参数外,有两个PCA类的成员值得关注。第一个是explained_variance_,它代表降维后的各主成分的方差值。方差值越大,则说明越是重要的主成分。第二个是explained_variance_ratio_,它代表降维后的各主成分的方差值占总方差值的比例,这个比例越大,则越是重要的主成分。
inputfile = 'data/principal_component.xls'
outputfile = 'tmp/dimention_reducted.xls' #降维后的数据
data = pd.read_excel(inputfile) #读入数据
pca = PCA()
pca.fit(data)
print(pca.components_) #返回模型的各个特征向量
print(pca.explained_variance_ratio_ )#返回各个成分各自的方差百分比

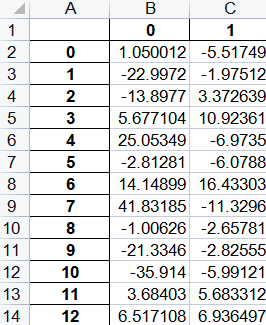
从上面结果来看得到特征方程det(R-λE)=0有7个特征根,对应7个单位特征向量以及各个成分的方差百分比(也成为了贡献率)。其中方差百分比越大,说明向量的权重越大。
当选取前3个主成分时,累计贡献率已经达到98.78%,说明选取前2个主成分进行计算已经相当不错,因此可以重新建立PCA模型,设置n_components=2,计算出成分结果。
pca=PCA(2)
pca.fit(data)
low_d=pca.transform(data)# 用它来降低纬度
pd.DataFrame(low_d).to_excel(outputfile)# 保存结果
pca.inverse_transform(low_d) #必要是可以用inverse_transform()函数来复原数据
降维结果
原始数据从8维被降到了2维,关系式由公式![]()
确定,同时这2维数据占原始数据95%以上的信息。
数值规约
数值规约通过选择替代的、较小的数据来减少数据量。数值规约可以是有参的,也可以是无参的。有参方法是使用一个模型来评估数据,只需存放参数,而不需要存放实际数据。有参的数值规约技术主要有两种:回归(线性回归和多元回归)和对数线性模型(近似离散属性集中的多维概率分布)。数值规约常用方法有直方图、用聚类数据表示实际数据、抽样(采样)、参数回归法。