朴素贝叶斯和AODE算法详解
文章目录
-
- 一、实验要求
-
- (1)实验目的
- (2)数据集简介
- (3)实验内容
- (4)评价指标
- 二、数据集的划分
- 三、朴素贝叶斯
-
- (1)朴素贝叶斯原理
- (2)拉普拉斯修正
- (3)函数变量解析
- (4)代码如下
- (5)结果
- 四、AODE算法
-
- (1)AODE算法原理
- 五、结果
-
- (1)acc结果对比
- (2)结果分析
- 参考
一、实验要求
(1)实验目的
- 1、掌握朴素贝叶斯分类器(Naïve Bayes Classifier, NBC)。
- 2、掌握AODE(Averaged One-Dependent Estimator)分类器
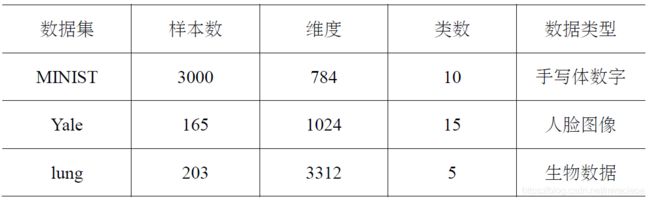
(2)数据集简介
(3)实验内容
- 1、编写程序实现朴素贝叶斯分类器设计。
- 2、编写程序实现AODE 分类器设计。
(4)评价指标
- 本次实验主要利用Acc 指标对聚类结果进行评价,值越大表明分类效果越好。
二、数据集的划分
- 将数据集8:2划分为训练集和测试集
- dataset_parse.py
import os
import numpy as np
from scipy.io import loadmat
from sklearn.model_selection import train_test_split
np.set_printoptions(threshold=np.inf)
# 数据准备
minist_path = r".\datasets\MNIST.mat"
lung_path = r".\datasets\lung.mat"
yale_path = r".\datasets\Yale.mat"
# 存储路径
PATH_MINIST = './data/minist/'
PATH_LUNG = './data/lung/'
PATH_YALE = './data/yale/'
# 加载数据
def create_data(path):
data = loadmat(path)
data_x = data["X"]
data_y = data["Y"][:, 0]
data_y -= 1
Data = np.array(data_x)
Label = np.array(data_y)
return Data, Label
def save_data(path, save_path):
X, y = create_data(path)
train_data, test_data, train_label, test_label = train_test_split(X, y, test_size=0.2, random_state=233)
if not os.path.exists(save_path):
os.makedirs(save_path)
np.savetxt(save_path + 'train_data.txt', train_data)
np.savetxt(save_path + 'train_label.txt', train_label)
np.savetxt(save_path + 'test_data.txt', test_data)
np.savetxt(save_path + 'test_label.txt', test_label)
if __name__ == '__main__':
save_data(yale_path, PATH_YALE)
save_data(lung_path, PATH_LUNG)
save_data(minist_path, PATH_MINIST)
print('完成')
三、朴素贝叶斯
(1)朴素贝叶斯原理
P ( 类 别 ∣ 特 征 1 , 特 征 2 , . . . ) = P ( 特 征 1 , 特 征 2 , . . . ∣ 类 别 ) ∗ P ( 类 别 ) P ( 特 征 1 , 特 征 2... ) = P ( 特 征 1 ∣ 类 别 ) ∗ P ( 特 征 2 ∣ 类 别 ) ∗ . . . P ( 特 征 1 ) ∗ P ( 特 征 1 ) ∗ . . . P(类别|特征1,特征2,...) = \frac{P(特征1,特征2,...|类别) * P(类别)}{P(特征1,特征2...)}=\frac{P(特征1|类别)*P(特征2|类别)*...}{P(特征1)*P(特征1)*...} P(类别∣特征1,特征2,...)=P(特征1,特征2...)P(特征1,特征2,...∣类别)∗P(类别)=P(特征1)∗P(特征1)∗...P(特征1∣类别)∗P(特征2∣类别)∗...
- 朴素贝叶斯的基本思想是假设所有属性都是相互独立的情况下,其中:
- 类别为将要识别分类的数据集的标签类别数,特征为分类数据的特征向量。
- P ( 特 征 n ∣ 类 别 ) = P ( 特 征 n , 类 别 ) P ( 类 别 ) P(特征n|类别) = \frac{P(特征n,类别)}{P(类别)} P(特征n∣类别)=P(类别)P(特征n,类别) : 在该类别发生的情况下,是所求的特征的概率 。比如类别0的情形下,类别0和特征同时满足的概率。
- P ( 类 别 ) P(类别) P(类别) : 每种类别在标签集中的比例,即每种标签的概率。
- P ( 特 征 1 ) + P ( 特 征 2 ) + . . . P(特征1)+P(特征2)+... P(特征1)+P(特征2)+... : 即每一个特征发生的概率,求和。
- 因为对于一个样本来说, P ( 特 征 1 ) ∗ P ( 特 征 1 ) ∗ . . . P(特征1)*P(特征1)*... P(特征1)∗P(特征1)∗...一样,分母一样,只要比较分子就好了。所以只要计算条件概率p(xk|y=j)和p(y= j)的先验概率,不需要计算 P ( 特 征 1 ) ∗ P ( 特 征 1 ) ∗ . . . P(特征1)*P(特征1)*... P(特征1)∗P(特征1)∗...。
- 由于最后要比较每个样本在m类标签各自的概率,然后取其中最大的,而且要计算 P ( 特 征 1 , 特 征 2 , . . . ∣ 类 别 ) ∗ P ( 类 别 ) P(特征1,特征2,...|类别) * P(类别) P(特征1,特征2,...∣类别)∗P(类别),不妨对其各自取对数,将其结果相加,比大小就可。
(2)拉普拉斯修正
- 根据训练集,算条件概率P(xk|y=j) 和先验概率 P(y=j),由于这两种概率可能会为0,后面无法计算,因此一定要进行Laplace平滑,代码就一句话,分子+1,分母+种类数。
P ( 类 别 m ) = D ( 类 别 m ) + 1 D + N P(类别m) = \frac{ D(类别m) + 1}{D+N} P(类别m)=D+ND(类别m)+1 - 其中D(类别m)为类别为m的数目,D为标签总数,N为标签类别数
P ( 特 征 n ∣ 类 别 m ) = D ( 特 征 n , 类 别 m ) + 1 D ( 类 别 m ) + N n P(特征n|类别m) = \frac{ D(特征n,类别m) + 1}{D(类别m)+N_{n}} P(特征n∣类别m)=D(类别m)+NnD(特征n,类别m)+1 - 其中D(类别m)为类别为m的数目,D(特征n,类别m)为特征n且为类别m的数目维数为 m ∗ n m*n m∗n, N n N_{n} Nn
为第n个特征数量,即一共有多上个不同值的特征,如果是minist数据集,数据集有784维,则有必要对其二值化,变为0和1,这样 N n N_{n} Nn的值就为2,便于简化计算。
(3)函数变量解析
- P ( y = j ) : P ( 类 别 ) P(y=j):P(类别) P(y=j):P(类别)
- P ( x k ∣ y = j ) : P ( 类 别 ∣ 特 征 ) P(x_{k}|y=j):P(类别|特征) P(xk∣y=j):P(类别∣特征)
- P ( y = j ∣ x k ) : P ( 特 征 ∣ 类 别 ) P(y=j|x_{k}) : P(特征|类别) P(y=j∣xk):P(特征∣类别)
- num::2400,特征的数目
- dimsnum:784,特征的维数
- labelnum:10,标签类别数
- pyj:1x10的零向量,代表 P ( y = j ) : P ( 类 别 ) P(y=j):P(类别) P(y=j):P(类别)
- pyjk1:10x784的零向量,代表 P ( y = j ∣ x k ) : P ( 特 征 ∣ 类 别 ) P(y=j|x_{k}) : P(特征|类别) P(y=j∣xk):P(特征∣类别)
- b=np.argmax(a)#取出a中元素最大值所对应的索引(索引值默认从0开始)
- b=np.argmax(a, axis=0)#对二维矩阵来讲a[0][1]会有两个索引方向,第一个方向为a[0],默认按列方向搜索最大值
- xk=0时,概率为1 - pyjxk1 ,xk=1时,概率为pyjxk1
- 坑:由于yale数据集只有203个,但是有15维,在程序中使用
for j in range(1+np.max(test_label)):来做循环,而不是for j in range(labelnum),由于样本量太少,导致在测试集里面没有某一类的样本,循环次数少了一次,导致精确度一直只有0.12。
(4)代码如下
- naive_bayes.py
import numpy as np
from data_handle import load_data, PATH_MINIST, PATH_LUNG, PATH_YALE
np.set_printoptions(threshold=np.inf)
# p(类别|特征) = p(特征|类别)*p(类别)/p(特征)
def normalize(data): ##将图片像素二值化
m, n = np.array(data).shape
h = (np.max(data) - np.min(data)) / 2
for i in range(m):
for j in range(n):
if data[i, j] > h:
data[i, j] = 1
else:
data[i, j] = 0
return data
def CalProb(train_data, train_label):
# p(y=j):p(类别) P(xk|y=j):p(特征|类别)
# 根据训练集 算条件概率P(xk|y=j) 和先验概率 P(y=j) 注意这两种概率可能会为0 后面无法计算 因此一定要进行Laplace平滑 参见李航P51
# num: 2400, dimsnum: 784
num, dimsnum = train_data.shape
# labelnum: 标签类别数
labelnum = len(set(train_label))
# pyj:1x10的零向量
pyj = np.zeros(labelnum)
# pyjk1:10x784的零向量
pyjk1 = np.zeros((labelnum, dimsnum))
# num: 2400
for i in range(num):
# 计算出每种标签的个数 ---> p(y=j):p(类别)
label = train_label[i]
# 需要laplace平滑 这里是真实个数
pyj[label] = pyj[label] + 1
# dimsnum: 784
for j in range(dimsnum):
# 因为会出现条件概率为0的情况 log无法计算 需要laplace平滑 ##算 Pj k = 1
# 此处计算的是所有label为1的数的个数
pyjk1[label][j] += train_data[i][j]
# print('pyj个数:', pyj)
# 条件概率 需要Laplace平滑 分母要加上xk的种类数 这里只能取0 1像素
# P y = j && xk = 1的概率 经验主义用频率去估计概率
# 此时pyj为10种类别各自的数目
# ni 为特征n的标签数
pyjk1 = (pyjk1.T + 1) / (pyj + 2)
# P y = j 的概率 先验概率 需要 Laplace平滑 分母要加上y的标签种类数
pyj = (pyj + 1) / (num + labelnum)
# pk1, #, pyjk1
return pyj, pyjk1
def CalTestProb_xk_yj(xk, pyjxk1): # 计算条件概率 P(xk|y=j)的概率的log
# xk=0时,概率为1 - pyjxk1 ,xk=1时,概率为pyjxk1
return xk * np.log(pyjxk1) + (1 - xk) * np.log(1 - pyjxk1)
# test 这块计算 应该可以优化
def test(test_data, test_label, pyjk1, pyj): # 测试
# num : 600 , dimsnum : 784
num, dimsnum = test_data.shape
labelnum = len(set(test_label))
acc = 0
for i in range(num):
testdata = test_data[i]
# 第i个样本属于j类的概率
p_yj_xi = np.log(pyj)
# 计算xi 属于 第j个类别的概率
for j in range(1+np.max(test_label)):
for k in range(dimsnum):
xk = testdata[k] # x^i的第j个像素 或者说是 维度
# print(pyjk1[j][k])
p_yj_xi[j] += CalTestProb_xk_yj(xk, pyjk1[j][k])
# p_yj_xi
# np.argmax : 取出a中元素最大值所对应的索引,此时最大值位6,其对应的位置索引值为4,(索引值默认从0开始)
p_y_xi = np.argmax(p_yj_xi)
acc += (p_y_xi == test_label[i])
# print('real is: ', test_label[i], ' predict is: ', p_y_xi)
print('Test accuracy is: ', acc / num)
def main(path):
train_data, test_data, train_label, test_label = load_data(path)
train_data = normalize(train_data)
test_data = normalize(test_data)
pyj, pyjk1 = CalProb(train_data, train_label)
test(test_data, test_label, pyjk1.T, pyj)
if __name__ == "__main__":
print('minist:')
main(PATH_MINIST)
print('---------')
print('lung')
main(PATH_LUNG)
print('---------')
print('yale')
main(PATH_YALE)
(5)结果
minist:
Test accuracy is: 0.8266666666666667
---------
lung
Test accuracy is: 0.926829268292683
---------
yale
Test accuracy is: 0.42424242424242425
四、AODE算法
(1)AODE算法原理
- 由于属性之间是相互独立的假设太强在现实生活中很难满足,故不妨对独立性条件进行放松—半朴素贝叶斯分类器,适当考虑一部分属性间的相互依赖信息,最常用的是独依赖,即每个属性最多依赖一个其他属性。
- AODE是一种基于集成学习机制、更为强大的独依赖分类器,其相关的计算公式如下:
P ( 类 别 m , 特 征 i ) = D ( 类 别 m , 特 征 i ) + 1 D + N ∗ N i P(类别m,特征i) = \frac{ D(类别m,特征i) + 1}{D+N*N_{i}} P(类别m,特征i)=D+N∗NiD(类别m,特征i)+1 - 其中D(类别m,特征i)为类别为m且在第i个特征上取值为 特征i 的数目,D为标签总数,N为标签类别数, N i N_{i} Ni为第i个特征可能的取值数
P ( 特 征 j ∣ 类 别 m , 特 征 i ) = D ( 特 征 j , 特 征 i , 类 别 m ) + 1 D ( 类 别 m , 特 征 i ) + N j P(特征j|类别m,特征i) = \frac{ D(特征j,特征i,类别m) + 1}{D(类别m,特征i)+N_{j}} P(特征j∣类别m,特征i)=D(类别m,特征i)+NjD(特征j,特征i,类别m)+1
- 其中D(特征j,特征i,类别m)为类别为m且在第i和第j个属性上取值分别为特征i和特征j的数目,D(类别m,特征i)为在类别m上,且取值为特征i的数目, N j N_{j} Nj为第j个特征可能取值的个数。
五、结果
(1)acc结果对比
| 数据/方法 | minist | lung | yale |
|---|---|---|---|
| bayes | 0.826 | 0.926 | 0.424 |
(2)结果分析
- 通过实验可以发现由于lung数据集的数据量最大,标签类别只有5,因此每一类标签的训练数据集较大,因此结果较高,可以到百分之九十,yale数据量小,标签类别为15,因此每一类标签的训练数据集较小,结果也相对较差。可以通过优化模型,或者增加数据记得方式来提高精确度。
- 在本次实验中,贝叶斯方法在lung数据集上效果最好,虽然比cnn要差了一些,但是在没有涉及神经网络的领域,精度已经较高了。
参考
神奇的拉普拉斯平滑(Laplacian Smoothing)及其在正则化上的应用~
谈谈自己对正则化的一些理解~
拉普拉斯修正的朴素贝叶斯分类器及AODE分类器
Python 机器学习_基于朴素贝叶斯分类的MNIST手写数字识别 - 本文的代码原型来源
详解朴素贝叶斯分类算法 - 用男生的特征来决定女生嫁不嫁,讲的生动有趣
贝叶斯分类器(一):朴素贝叶斯分类器与半朴素贝叶斯分类器 - 讲了很多贝叶斯相关原理