DynamicHead:基于注意力的统一目标检测头CVPR2021
目录
- 研究动机
- 方法
Dynamic Head是首个突破COCO数据集上单模型表现超越60AP的方法,来自论文:Dynamic Head: Unifying Object Detection Heads with Attentions,提出使用多重注意力机制统一物体检测头方法,通过在三个不同的角度(尺度感知、空间位置、多任务)分别运用注意力机制,在不增加计算量的情况下显著提升模型目标检测头的表达能力。这种新的实现方式,提供了一种可插拔特性,并提高多种目标检测框架的性能。
研究动机
首先对现有主流目标检测头的改进工作进行了总结,发现近期方法主要通过三个不同的角度出发进行目标检测性能的提升:
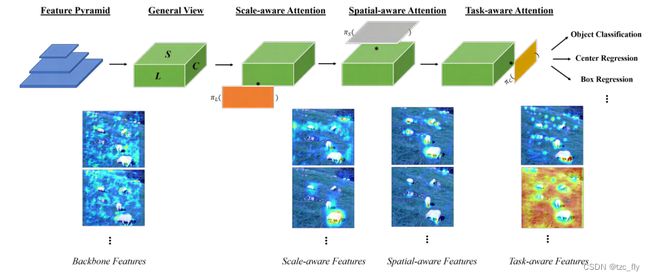
• 尺度感知scale-aware: 目标尺度的差异对应了不同尺度的特征,改进不同尺度级别的表达能力可以有效提升目标检测器的尺度感知能力,比如金字塔卷积方法;
• 空间位置spatial-aware:不相似目标形状的不同几何变换对应了特征的不同空间位置,改进不同空间位置的表达能力可以有效提升目标检测器的空间位置感知能力,比如最近的变形卷积方法;(同一个对象可以有不同的观察视角,导致呈现状态不同)
• 多任务task-aware:目标表达与任务的多样性对应了不同通道特征,改进不同通道的表达能力可以有效提升目标检测的任务感知能力。其中包括多任务学习(目标检测和分割任务),以及将目标检测输出转化成基于目标框,或者目标中心,或者关键点检测问题,从而获得更好的表达。(任务的多样性)

为此,作者希望设计一个统一的框架,提高目标检测Head的表达能力。
说到注意力机制,不得不提及在自然语言处理问题中已经广泛运用的transformer。它通过应用多头全连接层来学习交叉注意力,并从不同模式中融合特征。这种行为可以被视为在我们的表示中对空间和通道两个子维度进行建模。此外,最近的基于变形卷积的网络,广泛地运用到骨干网,这里如果将其运用到头,可以视为仅对空间子维度进行建模。这些方式多多少少存在一些片面性。
此文之所以称为动态头,还和最近比较流行的动态网络设计有关联。主要的设计思想是,网络的中间参数和输入的特征密切相关。这种方式可以极佳地利用有限网络容量获取更为普适性的表达。当训练数据增多后,性能会得到进一步大幅提高。
方法
从类似金字塔的backbone获得一组不同尺度(共 L L L个不同level的尺度)的特征 F i n = { F i } i = 1 L F_{in}=\left\{F_{i}\right\}_{i=1}^{L} Fin={Fi}i=1L,我们可以利用up-sampling和down-sampling对尺度进行调整。重新缩放的特征金字塔表示为四维张量 F ∈ R L × H × W × C F\in R^{L\times H\times W\times C} F∈RL×H×W×C,进一步,我们定义 S = H × W S=H\times W S=H×W,特征被reshape到 F ∈ R L × S × C F\in R^{L\times S\times C} F∈RL×S×C,基于这个表示,下面依次是每个维度的意义:
- 物体尺度的差异与不同level的特征有关。改进不同级别 F F F的表示学习可以有助于目标检测的尺度感知;
- 不同物体形状的各种几何变换与不同空间位置的特征相关。改进 F F F在不同空间位置的表示学习可以提高目标检测的空间感知能力;
- 不同的object representations和task可以与不同通道相关。改进 F F F不同通道的表征学习可以提高目标检测的任务感知。
- Dynamic Head方法的示例。它包含三种不同的注意力机制,每种机制侧重于不同的视角:尺度感知、空间感知和任务感知。上图可视化了在每个注意模块之后,特征图是如何改进的。
给定 F F F,自注意力的公式表示为: W ( F ) = π ( F ) ⋅ F W(F)=\pi(F)\cdot F W(F)=π(F)⋅F其中, π ( ⋅ ) \pi(\cdot) π(⋅)是注意力函数,朴素的注意力函数解决方案是通过全连接层来实现的。但是,由于张量的高维度,直接学习所有维度的注意力的计算成本很高。
相反,我们将注意力函数转换为三个连续的注意力,每个注意力只关注一个视角: W ( F ) = π C ( π S ( π L ( F ) ⋅ F ) ⋅ F ) ⋅ F W(F)=\pi_{C}(\pi_{S}(\pi_{L}(F)\cdot F)\cdot F)\cdot F W(F)=πC(πS(πL(F)⋅F)⋅F)⋅F其中, π L , π S , π C \pi_{L},\pi_{S},\pi_{C} πL,πS,πC是三个不同的注意力函数,分别用于维度 L , S , C L,S,C L,S,C。
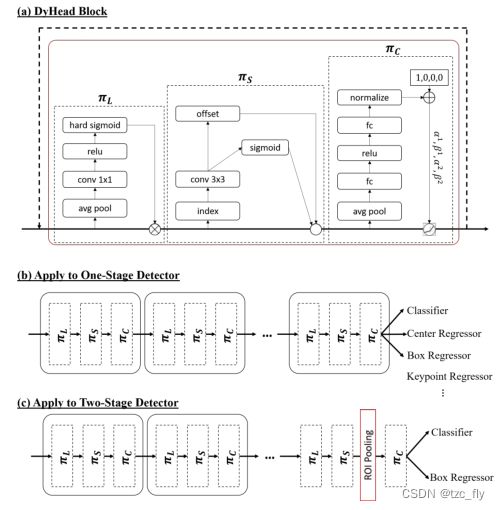
Scale-aware attention π L \pi_{L} πL:我们首先引入一种尺度感知注意力,根据不同尺度的语义重要性动态融合不同尺度的特征。 π L ( F ) ⋅ F = σ ( f ( 1 S C ∑ S , C F ) ) ⋅ F \pi_{L}(F)\cdot F=\sigma(f(\frac{1}{SC}\sum_{S,C}F))\cdot F πL(F)⋅F=σ(f(SC1S,C∑F))⋅F其中, f ( ⋅ ) f(\cdot) f(⋅)是一个1×1卷积层实现的线性近似, σ ( x ) = m a x ( 0 , m i n ( 1 , x + 1 2 ) ) \sigma(x)=max(0,min(1,\frac{x+1}{2})) σ(x)=max(0,min(1,2x+1))是一个hard-sigmoid函数。
Spatial-aware attention π S \pi_{S} πS:我们应用另一个基于融合特征的空间感知注意模块来关注空间位置和特征level之间一致共存的判别区域。考虑到 S S S的高维性,我们将此模块分解为两个步骤:首先使用可变形卷积使注意力学习判别区,然后在相同空间位置跨level聚合特征: π S ( F ) ⋅ F = 1 L ∑ l = 1 L ∑ k = 1 K w l , k ⋅ F ( l ; p k + Δ p k ; c ) ⋅ Δ m k \pi_{S}(F)\cdot F=\frac{1}{L}\sum_{l=1}^{L}\sum_{k=1}^{K}w_{l,k}\cdot F(l;p_{k}+\Delta p_{k};c)\cdot\Delta m_{k} πS(F)⋅F=L1l=1∑Lk=1∑Kwl,k⋅F(l;pk+Δpk;c)⋅Δmk其中, K K K是稀疏采样的位置数量, p k + Δ p k p_{k}+\Delta p_{k} pk+Δpk是偏移后的位置, Δ m k \Delta m_{k} Δmk是位置 p k p_{k} pk的重要程度。
Task-aware attention π C \pi_{C} πC:为了实现联合学习并泛化object的不同任务表示,在最后部署了任务感知注意力。它动态切换特征的开启和关闭通道,以支持不同的任务: π C ( F ) ⋅ F = m a x ( α 1 ( F ) ⋅ F c + β 1 ( F ) , α 2 ( F ) ⋅ F c + β 2 ( F ) ) \pi_{C}(F)\cdot F=max(\alpha^{1}(F)\cdot F_{c}+\beta^{1}(F),\alpha^{2}(F)\cdot F_{c}+\beta^{2}(F)) πC(F)⋅F=max(α1(F)⋅Fc+β1(F),α2(F)⋅Fc+β2(F))其中, F c F_{c} Fc是特征在第 c c c通道的切片, [ α 1 , α 2 , β 1 , β 2 ] = θ ( ⋅ ) [\alpha^{1},\alpha^{2},\beta^{1},\beta^{2}]=\theta(\cdot) [α1,α2,β1,β2]=θ(⋅)是一个学习控制激活阈值的函数, θ ( ⋅ ) \theta(\cdot) θ(⋅)首先在 L × S L×S L×S维上进行全局平均pooling以降低维数,然后使用两个全连接层和一个归一化层,最后应用移位的sigmoid函数将输出归一化为 [ − 1 , 1 ] [−1, 1] [−1,1]。
最后,由于上述三种注意机制是顺序应用的,我们可以多次嵌套,以有效地将多个 π L π_{L} πL、 π S π_S πS和 π C π_C πC块叠加在一起。下图a显示了Dynamic head的详细配置。
- Dynamic head的详细设计。a显示了每个注意模块的详细实现。b显示了如何将动态头块应用于1 stage检测器。c演示如何将动态头块应用于2 stage检测器。