哈工大2022机器学习实验二：逻辑回归

本实验要求利用逻辑回归（Logistic Regression），对生成的数据进行二分类。首先我们先回顾一下逻辑回归的基本原理：

逻辑回归

逻辑回归，又意译为对率回归（周志华《机器学习》），虽然它的名字中带“回归”，但它是一个分类模型。它的基本思想是直接估计条件概率$P(Y|X)$的表达式，即给定样本$X=x$（这里$x$是一个$d$维列向量），其属于类别$Y$的概率（这里研究的是二分类问题，$Y$的取值只有$0,1$，$1$表示正例，$0$表示反例）。利用贝叶斯公式，可以得到给定样本，其为正例的概率
$$\begin{array}{rl}P(Y=1|X=x)& =\frac{P(X=x|Y=1)P(Y=1)}{P(X=x)}\\ & =\frac{P(X=x|Y=1)P(Y=1)}{P(X=x|Y=1)P(Y=1)+P(X=x|Y=0)P(Y=0)}\\ & =\frac{1}{1+\frac{P(X=x|Y=0)P(Y=0)}{P(X=x|Y=1)P(Y=1)}}\end{array}$$
在这个式子中有两类式子需要我们已知：类别先验$P(Y=y)$和条件分布$P(X|Y)$.这也是逻辑回归做出的最基本假设：

（1）类别先验服从伯努利分布$B(1,p),$即一个样本有$p$的概率为正例。
（2）类内样本服从正态分布$N(\mu ,\Sigma ).$具体地说，正例样本服从$N({\mu }_1,{\Sigma }_1)$；反例样本服从$N({\mu }_0,{\Sigma }_0)$。特别地，我们要求两类样本的协方差矩阵相同，即${\Sigma }_1={\Sigma }_0=\Sigma .$之后我们就都用$\Sigma$这一个符号代表协方差矩阵。

（注：$n$维正态分布$N(\mu ,\Sigma )$的概率密度$p(x)=\frac{1}{(2\pi {)}^{n/2}|\Sigma {|}^{1/2}}\exp \{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\}$）

顺着上面两条假设，我们可以继续推导。我们在这里用正态分布的概率密度来代替概率（这个推导在概率论中不是那么严谨，但概率密度的大小可以一定程度上反映样本分布在该点的概率大小。）
$$\begin{array}{rl}P(Y=1|X=x)& =\frac{1}{1+\frac{P(X=x|Y=0)P(Y=0)}{P(X=x|Y=1)P(Y=1)}}\\ & =\frac{1}{1+\frac{\exp \{-\frac{1}{2}(x-{\mu }_0{)}^T{\Sigma }^{-1}(x-{\mu }_0)\}}{\exp \{-\frac{1}{2}(x-{\mu }_1{)}^T{\Sigma }^{-1}(x-{\mu }_1)\}}\cdot \frac{p}{1-p}}\\ & =\frac{1}{1+\exp \{({\mu }_0-{\mu }_1{)}^T{\Sigma }^{-1}x+\frac{1}{2}({\mu }_1^T{\Sigma }^{-1}{\mu }_1-{\mu }_0^T{\Sigma }^{-1}{\mu }_0)\}\cdot \frac{p}{1-p}}\end{array}$$
上式2~3行就是把两个指数相除，把项展开整理了一下。我们把结果中的$\frac{p}{1-p}$也改写成指数形式：
$$\frac{p}{1-p}=\exp \ln (\frac{p}{1-p})$$
再整理一下$P(Y=1|X=x),$得到
$$P(Y=1|X=x)=\frac{1}{1+\exp \{({\mu }_0-{\mu }_1{)}^T{\Sigma }^{-1}x+\frac{1}{2}({\mu }_1^T{\Sigma }^{-1}{\mu }_1-{\mu }_0^T{\Sigma }^{-1}{\mu }_0)+\ln \frac{p}{1-p}\}}$$
这时我们设
$$\begin{gathered} w=({\Sigma }^{-1}{)}^T({\mu }_0-{\mu }_1)=(w_1,w_2,...,w_d{)}^T\in {\mathbb{R}}^{d\times 1}, \\ b=\frac{1}{2}({\mu }_1^T{\Sigma }^{-1}{\mu }_1-{\mu }_0^T{\Sigma }^{-1}{\mu }_0)+\ln \frac{p}{1-p}\in \mathbb{R}, \end{gathered}$$
就得到了逻辑回归最经典的形式
$$P(Y=1|X=x)=\frac{1}{1+\exp (w^{T}x+b)}.$$
很多地方会把正例的条件概率写为
$$P(Y=1|X=x)=\frac{\exp (w^{T}x+b)}{1+\exp (w^{T}x+b)}=\frac{1}{1+\exp (-(w^{T}x+b))},$$
这两种写法实质上表示是等价的，只要把第一个式子上下同乘$\exp (-w^{T}x-b)$，再用$w^{\prime }=-w,b^{\prime }=-b$代换即可。为了后面推导的形式简便，我们采用第二种。（即分子上也带$\exp$的写法，这也是为什么Sigmoid函数$f(z)=\frac{1}{1+e^{-z}}$被用在这里）

整理一下我们得到的结论：假设正反两类样本（$d$维）满足：

（1）类别先验服从伯努利分布$B(1,p),$即一个样本有$p$的概率为正例；
（2）正例样本服从$N({\mu }_1,\Sigma )$；反例样本服从$N({\mu }_0,\Sigma )$。

那么我们可以得到，给定样本$X=x=(x_1,x_2,...,x_d{)}^T,$其属于正反两类的概率形如

$$P(Y=1|X=x)=\frac{\exp (w^{T}x+b)}{1+\exp (w^{T}x+b)},$$
$$P(Y=0|X=x)=\frac{1}{1+\exp (w^{T}x+b)}.$$
容易得到，$P(Y=1|X=x)>P(Y=0|X=x)$的条件为$\exp (w^{T}x+b)>1$即$w^{T}x+b>0.$因此我们的分界面是线性的，即$w^{T}x+b=0.$

因此，逻辑回归的任务就是在数据集$X,Y$（$Y$为每个样本对应的类别）上学习参数$w$和$b$，使其得到的概率与数据集最吻合。为了进行学习，我们采用最大似然估计：
$$\begin{array}{rl}w,b& =\underset{w,b}{\mathrm{argmax}}\prod _{i=1}^{N}P(X=x_i,Y=y_i)\\ & =\underset{w,b}{\mathrm{argmax}}\prod _{i=1}^{N}P(Y=y_i|X=x_i)P(X=x_i)\end{array}$$
由于$P(X=x_i)$与参数形式无关，可以去掉，即
$$w,b=\underset{w,b}{\mathrm{argmax}}\prod _{i=1}^{N}P(Y=y_i|X=x_i)$$
为了推导形式简洁，我们把$P(Y=y_i|X=x_i)$记为
$$\begin{array}{rl}P(Y=y_i|X=x_i)& =y_{i}P(Y=1|X=x_i)+(1-y_i)P(Y=0|X=x_i)\\ & =\frac{y_i\exp (w^{T}x+b)+1-y_i}{1+\exp (w^{T}x+b)}\end{array}$$
很容易验证，这个式子与我们得到的结论等价（$y_i=1$时，后一项不起作用；$y_i=0$时，前一项不起作用）。继续推导，得
$$\begin{array}{rl}w,b& =\underset{w,b}{\mathrm{argmax}}\prod _{i=1}^N\frac{y_i\exp (w^{T}x+b)+1-y_i}{1+\exp (w^{T}x+b)}\\ & =\underset{w,b}{\mathrm{argmax}}\sum _{i=1}^N\ln \frac{y_i\exp (w^{T}x+b)+1-y_i}{1+\exp (w^{T}x+b)}(取对数不改变最值点)\\ & =\underset{w,b}{\mathrm{argmax}}\sum _{i=1}^N[\ln (y_i\exp (w^{T}x+b)+1-y_i)-\ln (1+\exp (w^{T}x+b))]\\ & =\underset{w,b}{\mathrm{argmax}}\sum _{i=1}^N[y_i(w^{T}x+b)-\ln (1+\exp (w^{T}x+b))](观察第一项与上一项等价，分y_i=0,1讨论)\\ & =\underset{w,b}{\mathrm{argmin}}\sum _{i=1}^N[-y_i(w^{T}x+b)+ln(1+\exp (w^{T}x+b))](取相反数,变为\mathrm{argmin}).\end{array}$$
因此，学习$w,b$的任务就变为了最小化关于$w,b$的损失函数(其实就是负对数似然)
$$l=\sum _{i=1}^N[-y_i(w^{T}x+b)+ln(1+\exp (w^{T}x+b))]$$
为了让整体形式更简洁，我们重新设$x=(1,x_1,x_2,...,x_d{)}^T,\beta =(b,w_1,w_2,...,w_d{)}^T,$损失函数变为
$$l=\sum _{i=1}^N[-y_i{\beta }^{T}x+ln(1+e^{{\beta }^{T}x})].$$
该优化问题可以用梯度下降法/牛顿迭代法求解，只需求$l$关于$\beta$的偏导数，每次迭代减去该梯度$\times$学习率:
$$\frac{\partial l}{\partial \beta }=-\sum _{i=1}^N{x}_i(y_i-\frac{\exp ({\beta }^{T}x)}{1+\exp ({\beta }^{T}x)})$$

代码部分

下面我们来实现该过程。本次实验仍然采用python numpy库：

import numpy as np
import matplotlib.pyplot as plt

获取数据集

这次我们需要的数据集应当服从正态分布（见前面的讨论）。我们传入两类样本的均值和协方差，同时可以设置前面提到的类别先验$p$(在代码中为pi)，我这里默认设为0.3。此外，为了探究两类样本不满足协方差相同时的结果，我们也留一个可选参数cov2作为反例样本的协方差。

'''
获取二分类问题数据集，两类数据均服从正态分布
- N 数据集大小，默认为100
- pi 正例的比例，默认为0.3
- mean 两类样本的均值，为2 * d 维矩阵，d为正态分布维数
- 例: [[1, 1], [3, 3]]表示正例样本均值为(1, 1), 反例样本为(3, 3)
- cov 协方差矩阵，为d * d维矩阵
- 例: [[1, 0], [0, 1]]
- cov2 用于测试不满足Logistic回归假设(不是朴素贝叶斯假设)时结果。若不传入该参数，两类样本协方差相同；否则cov2代表第二类样本的协方差。
'''
def get_dataset(mean, cov, N = 100, pi = 0.3, cov2 = None):
    mean = np.array(mean, dtype = 'float')
    cov = np.array(cov, dtype = 'float')
    assert mean.shape[0] == 2 and mean.shape[1] == cov.shape[0] and cov.shape[0] == cov.shape[1], '参数不合法!'
    positive = int(N *pi)
    negative = N - positive
    pdata = np.random.multivariate_normal(mean[0], cov, positive)
    ndata = np.random.multivariate_normal(mean[1], cov if cov2 is None else cov2, negative)
    return np.concatenate([pdata, ndata]), np.concatenate([np.ones(positive), np.zeros(negative)])

代码中np.concatenate用于把正例和反例拼接起来。最后返回的数据应该类似于(data, target),其中data形如
$$X=\left(\begin{array}{c}{x}_{11}\cdots x_{1d}\\ x_{21}\cdots x_{2d}\\ ⋮⋮\\ x_{N1}\cdots x_{Nd}\end{array}\right),$$
前$Np$行的样本（如$N=100,p=0.3$,那么就是前$30\%=30$行）是正例，其余样本为反例。target形如
$$Y=\left(\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_N\end{array}\right).$$
其中前$Np$行为$1$，剩余行为$0$.

梯度下降法

梯度下降法与上一篇博客基本类似。

'''
梯度下降法优化损失函数。
- data 数据集
- target 数据的标签，与数据集一一对应
- max_iteration 最大迭代次数，默认为10000
- lr 学习率，默认为0.05
'''
def GD(data, target, max_iteration = 10000, lr = 0.05):
	# 判断收敛的阈值
    epsilon = 1e-8
    # 意义如上文所述
    N, d = data.shape
    # 意义如上文所述，随机初始化后开始梯度下降
    beta = np.random.randn(d + 1)
    # 因为我们在前面加了一列1
    X = np.concatenate([np.ones((N, 1)), data], axis = 1)

    for i in range(max_iteration):
        term1 = -np.sum(X * target.reshape(N, 1), axis = 0)
        term2 = np.sum((1 / (np.e ** -np.dot(beta, X.T) + 1)).reshape(N, 1) * X, axis = 0)
        grad = term1 + term2
        if np.linalg.norm(grad) < epsilon:
            break
        beta -= lr * grad
    return beta

代码中的梯度（grad = term1 + term2）看上去非常难以理解，一般我们不会故意这么写，但numpy库中内置的函数往往比for循环快很多，所以我们尽可能用内置函数进行矩阵运算。稍微解释一下：我们之前算出来的梯度为
$$\frac{\partial l}{\partial \beta }=-\sum _{i=1}^N{x}_i(y_i-\frac{\exp ({\beta }^T{x}_i)}{1+\exp ({\beta }^T{x}_i)}).$$
我们把式子拆成两项：第一项是$-\sum _{i=1}^N{x}_i{y}_i,$其中$x_i$是向量（注意我们补了一列$1$），$y_i\in \{0,1\}$；而数据集
$$X=\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_N\end{array}\right),Y=\left(\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_N\end{array}\right).$$
利用numpy的*运算将对应行相乘，但在这之前我们需要把$Y$变成一个二维数组（利用reshape(N,1)），最后需要对相乘结果按行相加，这在numpy中用np.sum(A, axis=0)表示，这就是代码中term1的来历。

我们再看第二项$\sum _{i=1}^N{x}_i\frac{\exp ({\beta }^T{x}_i)}{1+\exp ({\beta }^T{x}_i)}$。
（1）首先我们计算$\exp ({\beta }^{T}x)$，可以直接用np.dot表示为np.dot(beta, X.T)；

（2）然后构造$\frac{\exp ({\beta }^T{x}_i)}{1+\exp ({\beta }^T{x}_i)}$这一项，为了防止重复运算我们把它变形成$\frac{1}{1+\exp (-{\beta }^T{x}_i)}$，代码中对应1 / (np.e ** -np.dot(beta, X.T) + 1)。注意这个结果是一个$N$维向量，每一维对应一个$x_i$的结果。

（3）之后我们只需要故技重施，把第$i$个分量与$x_i$对应相乘并相加即可，对应到代码中即np.sum((1 / (np.e ** -np.dot(beta, X.T) + 1)).reshape(N, 1) * X, axis = 0).

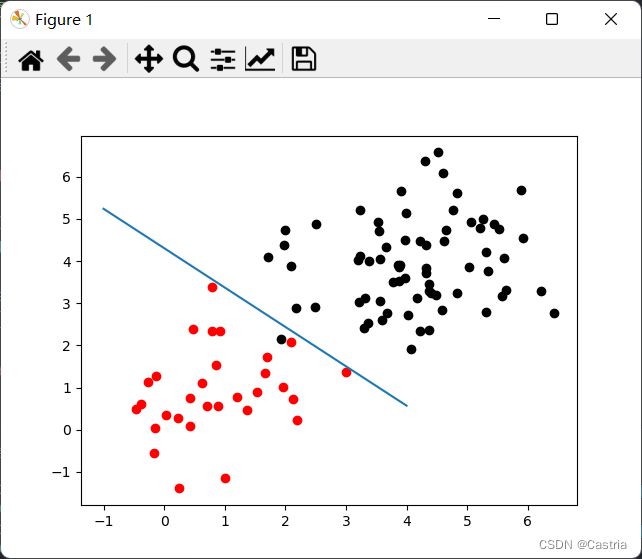
接下来我们写一个主函数验证结果。为了便于可视化，我们采用$2$维变量，当然为了升高维度只需要调整get_dataset的协方差矩阵维数和均值维数即可（注意形状要对上：均值维数为$2\times d,$协方差矩阵维数为$d\times d$）。主函数如下：

if __name__ == '__main__':
    mean = [[1, 1], [4, 4]]
    cov = np.diag([1, 1])

    data, target = get_dataset(mean, cov)

    beta = GD(data, target, max_iteration = 100000)

    for (x, y), label in zip(data, target):
        plt.scatter(x, y, c = 'red' if label else 'black')

    x = np.linspace(-1, 4)
    '''
    由于beta(d=2)形如(beta[0], beta[1], beta[2]),
    在二维空间中表示分界面为w^T*x+b=0,当x=(1, x, y)时(这里x, y指横纵坐标)
    分界面为beta[0]+beta[1]x+beta[2]y=0,或写成标准一次函数形式
    y=(-beta[1]x -beta[0]) / beta[2].
    '''
    y = (-beta[1] * x - beta[0]) / beta[2]

    plt.plot(x, y)
    plt.show()

其中一次结果如下：

过拟合&正则项

在训练模型过程中，为了防止模型复杂度过高，就像在最小二乘法中一样，我们也可以加入正则项$\lambda ||w|{|}^2=\lambda w^{T}w$来约束$w$的模长。修改后的梯度下降法只需要加入正则项的梯度即可：
$$\frac{\partial l}{\partial \beta }=-\sum _{i=1}^N{x}_i(y_i-\frac{\exp ({\beta }^T{x}_i)}{1+\exp ({\beta }^T{x}_i)})+2\lambda w.$$
其中的系数$2$可以忽略（可以通过调节$\lambda$得到同样的效果）。修改后的梯度下降法：

'''
梯度下降法优化损失函数。
- data 数据集
- target 数据的标签，与数据集一一对应
- max_iteration 最大迭代次数，默认为1000
- lr 学习率，默认为0.05
- l 正则项系数，默认不加正则项
'''
def GD(data, target, max_iteration = 10000, lr = 0.05, l = 0):
    epsilon = 1e-8
    N, d = data.shape
    beta = np.random.randn(d + 1)
    X = np.concatenate([np.ones((N, 1)), data], axis = 1)

    for i in range(max_iteration):
        term1 = -np.sum(X * target.reshape(N, 1), axis = 0)
        term2 = np.sum((1 / (np.e ** -np.dot(beta, X.T) + 1)).reshape(N, 1) * X, axis = 0)
        regularize = l * beta
        grad = term1 + term2 + regularize
        if np.linalg.norm(grad) < epsilon:
            break
        beta -= lr * grad
    return beta

我们再写两个辅助函数，来检验一下加入正则项后的效果：

# 根据模型beta预测x所属的类, 返回1(正例), 或0(反例)。
def predict(beta, x):
    return 1 if np.dot(beta[1:], x) + beta[0] > 0 else 0
# 评估整个数据集上的效果
def evaluate(beta, data, target):
    cnt = 0
    for x, y in zip(data, target):
        if predict(beta, x) == int(y):
            cnt += 1
    print(f'模型参数: {beta}')
    print(f'模型复杂度(模长): {np.linalg.norm(beta)}')
    print(f'预测准确率: {cnt / len(target)}')

下面是几次的运行结果：

模型参数: [-0.78524378 -3.34318712 -1.86253962] # 未正则化
模型复杂度(模长): 3.906732871506824
预测准确率: 0.95
模型参数: [-0.52418376 -2.10771474 -1.37132344] # 正则化
模型复杂度(模长): 2.56861013046
预测准确率: 0.95
----------------------------------------------
模型参数: [-0.73382186 -5.31193987 -5.03064085] # 未正则化
模型复杂度(模长): 7.352723791057766
预测准确率: 0.96
模型参数: [-0.5065628  -1.75035625 -2.09991419] # 正则化
模型复杂度(模长): 2.7802863999234253
预测准确率: 0.96
----------------------------------------------
模型参数: [-0.44133903 -3.04645754 -2.45359287] # 未正则化
模型复杂度(模长): 3.936470713612132
预测准确率: 0.95
模型参数: [-0.39689499 -1.91437456 -1.63920354] # 正则化
模型复杂度(模长): 2.5513415720325567
预测准确率: 0.96

可以看到正则化显著地降低了模型复杂度（即参数模长）。我们也可以从另一个场景来理解过拟合，这个场景更类似于上次实验中的最小二乘法。我们通过之前的推导，得到了逻辑回归得到的分界面是一个线性分界面（$w^{T}x+b=0$）。那么它只能得到（对于原变量的）线性分界面吗？如果我们拿到了如下的数据：

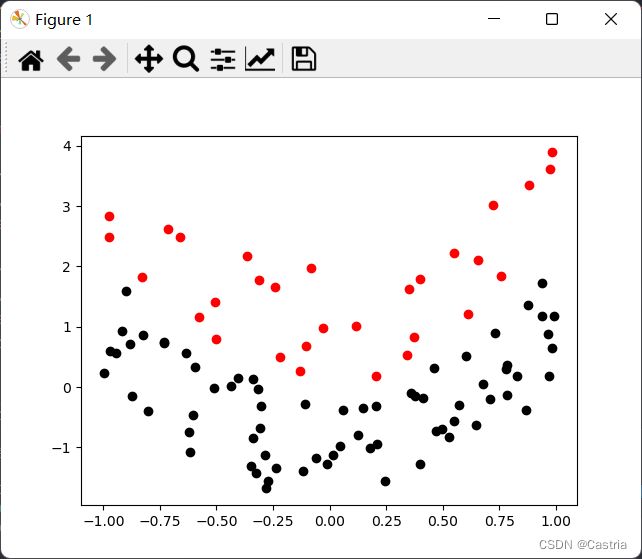
这个数据是用$y=2x^2$为分界面的。我们能不能用逻辑回归对其进行分类呢？我们如果不做任何处理，得到的分界面形如
$$ax+by+c=0$$
这时显然是无法正确分类的。但如果我们主动对数据进行升维，把原来的单个数据$(x,y)$变为$(x,y,x^2)$，再应用逻辑回归，得到的分界面当然就形如
$$ax+by+c{x}^2+d=0$$
这说明逻辑回归可以有与二次函数相同的表示能力。我们对这个数据集应用上述思想，得到结果

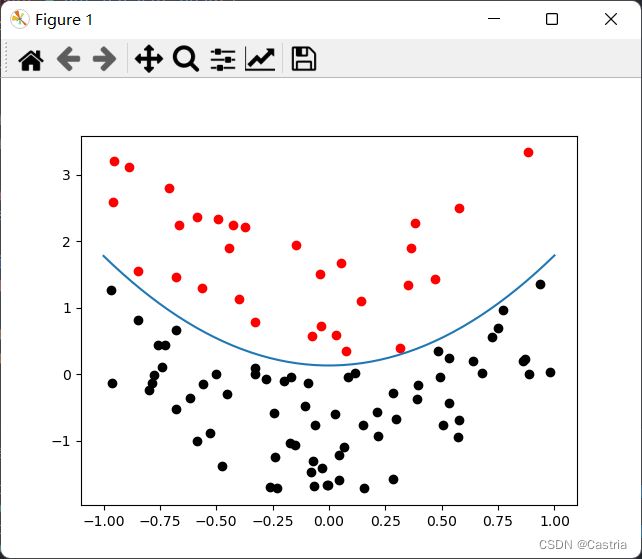
满足了我们的要求。这部分的额外代码如下：

def get_dataset_quad(N = 100, pi = 0.3):
    positive = int(N *pi)
    negative = N - positive
    data, target = [], []
    for i in range(positive):
        x = np.random.rand() * 2 - 1
        data.append([x, 2 * x * x + np.random.rand() * 2])
        target.append(1)
    for i in range(negative):
        x = np.random.rand() * 2 - 1
        data.append([x, 2 * x * x - np.random.rand() * 2])
        target.append(0)
    return np.array(data), np.array(target)
    
if __name__ == '__main__':
    mean = [[-1, -1], [1, 1]]
    cov = np.diag([1, 1])

    data, target = get_dataset()
    data = np.concatenate([data, (data[:, 0] ** 2).reshape(data.shape[0], 1)], axis = 1)

    beta = GD(data, target, lr = 0.01, max_iteration = 100000)

    for (x, y, x_2), label in zip(data, target):
        plt.scatter(x, y, c = 'red' if label else 'black')
    
    x = np.linspace(-1, 1)
    y = (-beta[3] * x * x - beta[1] * x - beta[0]) / beta[2]

    plt.plot(x, y)
    plt.show()

上面的例子使我们想到，如果我们拿到一组$d$维数据就对它进行升维，比如把$(x_1,x_2,...,x_d)$升维成$(x_1,x_2,...,x_d,x_1^2,x_2^2,...,x_d^2)$甚至更高次的函数，那逻辑回归的表示能力不就可以更强大吗？但此时就会遭遇过拟合问题，比如我们对上述的正态分布应用该思想，把$(x,y)$升维成$(x,y,x^2)$，得到结果如下：

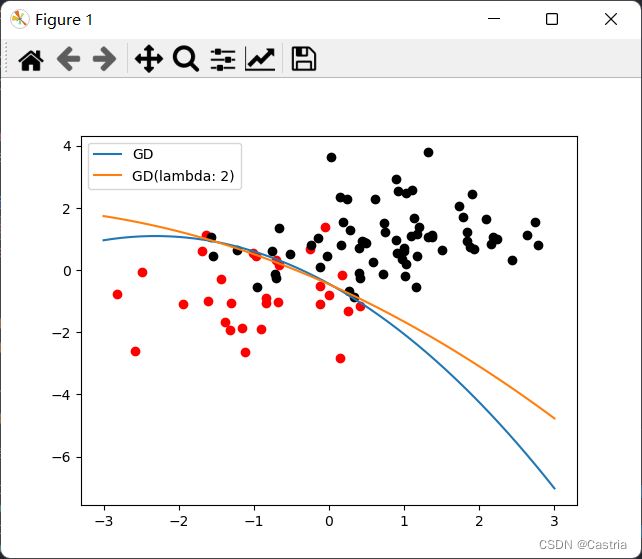
我们发现，原本的线性分类面被刻画成了二次函数，凭空增加了模型的复杂度，这是不合适的。因此，我们也可以通过加入正则项来“抑制”模型的表示能力，上图中橙色线就是正则项系数$\lambda =2$时的情况，可以明显地看出它更接近一条直线。得到上图的代码如下：

if __name__ == '__main__':
    mean = [[-1, -1], [1, 1]]
    cov = np.diag([1, 1])

    data, target = get_dataset(mean, cov)

    data = np.concatenate([data, (data[:, 0] ** 2).reshape(data.shape[0], 1)], axis = 1)

    beta1 = GD(data, target, lr = 0.01, max_iteration = 100000)
    beta2 = GD(data, target, lr = 0.01, max_iteration = 100000, l = 2)

    for (x, y, x_2), label in zip(data, target):
        plt.scatter(x, y, c = 'red' if label else 'black')
    
    x = np.linspace(-3, 3)
    y1 = (-beta1[3] * x * x - beta1[1] * x - beta1[0]) / beta1[2]
    y2 = (-beta2[3] * x * x - beta2[1] * x - beta2[0]) / beta2[2]
    

    plt.plot(x, y1, label = 'GD')
    plt.plot(x, y2, label = 'GD(lambda: 2)')

    plt.legend()
    plt.show()

最后我们再来讨论一下不满足朴素贝叶斯基本假设的情况。朴素贝叶斯假设各变量相互独立，即$\Sigma$为对角阵的情况。然而我们之前的假设并没有假设变量相互独立，所以违反该假设不应该影响我们模型的分类效果($\Sigma$应当是对称、半正定的，这是多元正态分布的要求)。我们简单地测试一下：

if __name__ == '__main__':
    mean = [[-1, -1], [1, 1]]
    cov = [[1.3, 1], [1, 0.8]]


    data, target = get_dataset(mean, cov)

    beta = GD(data, target, lr = 0.01, max_iteration = 100000)

    for (x, y), label in zip(data, target):
        plt.scatter(x, y, c = 'red' if label else 'black')
    
    x = np.linspace(-3, 3)
    y = (-beta[1] * x - beta[0]) / beta[2]
    

    plt.plot(x, y)

    plt.show()

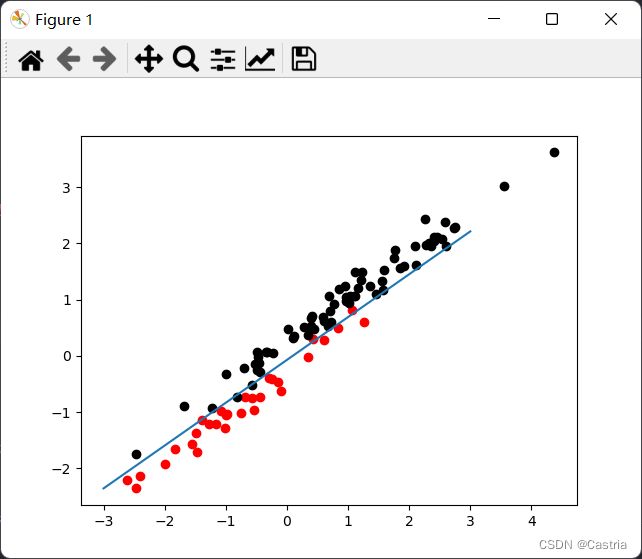
理论上，非对角的协方差矩阵让多个变量有了相关性，这种相关性体现在图像上就是对原来的图像进行了旋转，应当不影响分类问题的结果（我们只需要把分界面对应旋转即可）。