KL散度 JS散度 熵
KL散度 JS散度 熵
- 1.自信息和熵
-
- 1.1 自信息self information
- 1.2 熵 entropy
- 2.KL散度 Kullback-Leibler divergence
-
- 2.1 定义
- 2.2 KL散度与熵、交叉熵之间的关系
- 2.3 python代码实现
-
- 2.3.1 定义两个概率分布并可视化
- 2.3.2 计算KL散度
-
- 2.3.2.1 自定义函数
- 2.3.2.2 scipy自带函数
- 3.JS散度 Jensen-Shannon divergence
-
- 3.1 定义
- 3.2 python代码实现
- 4.交叉熵 cross-entropy
-
- 4.1 公式
- 4.2 python代码实现
- 参考文献
此blog可视为机器学习术语的部分内容。
有些术语,耳熟能详,但如果让细致表述下,却往往捉襟见肘,好似熟悉的陌生人,总结下时而温故。
1.自信息和熵
1.1 自信息self information
自信息表示一个随机事件包含的信息量,随机事件发生概率越高,自信息越低;发生概率越低,自信息越高。
设一随机变量X,事件x发生的概率为 p ( x ) p(x) p(x),则自信息定义为:
I ( x ) = − log p ( x ) \qquad\qquad\qquad\qquad\qquad\qquad I(x)=-\log p(x) I(x)=−logp(x).
1.2 熵 entropy
熵是表示随机变量不确定性的度量。
离散随机变量X的概率分布为:
P ( X = x i ) = p i , i = 1 , 2 , . . . , n \qquad\qquad\qquad P(X=x_i)=p_i,i=1,2,...,n P(X=xi)=pi,i=1,2,...,n
其熵定义为:
H ( X ) = − ∑ i p i log p i \qquad\qquad\qquad H(X)=-\sum\limits_ip_i\log p_i H(X)=−i∑pilogpi
可见熵只依赖于随机变量的分布,与随机变量的值无关,因此 H ( X ) H(X) H(X)也记作 H ( p ) H(p) H(p)。
若随机变量X只有两个取值,1和0,则X的分布为:
P ( X = 1 ) = p , P ( X = 0 ) = 1 − p , p ∈ [ 0 , 1 ] \qquad\qquad\qquad P(X=1)=p, \ P(X=0)=1-p,p \in[0,1] P(X=1)=p, P(X=0)=1−p,p∈[0,1],此时熵为:
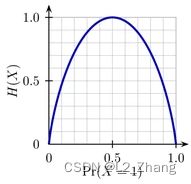
H ( X ) = − p log p − ( 1 − p ) log ( 1 − p ) \qquad\qquad\qquad H(X)=-p\log p-(1-p)\log(1-p) H(X)=−plogp−(1−p)log(1−p)
可见当 p = 0 或 1 p=0或1 p=0或1时, H ( x ) H(x) H(x)均为0 ,即没有不确定性。
p = 0.5 p=0.5 p=0.5时, H ( x ) = 1 H(x)=1 H(x)=1,取得最大值 ( log 以 2 为底 \log以2为底 log以2为底)。
2.KL散度 Kullback-Leibler divergence
2.1 定义
K L ( P ∥ Q ) = ∑ x p ( x ) log p ( x ) q ( x ) = − ∑ x p ( x ) log q ( x ) p ( x ) \qquad\qquad KL(P \parallel Q) = \sum\limits_{x}p(x)\log\cfrac{p(x)}{q(x)}=- \sum\limits_{x}p(x)\log\cfrac{q(x)}{p(x)} KL(P∥Q)=x∑p(x)logq(x)p(x)=−x∑p(x)logp(x)q(x)
其中 p , q p,q p,q是两个概率分布,KL散度可用来衡量两个分布之间的差异。
KL散度满足非负性,即 K L ( P ∥ Q ) ≥ 0 KL(P \parallel Q)\ge0 KL(P∥Q)≥0。
当这两个分布完全一致时,KL散度值为0。
2.2 KL散度与熵、交叉熵之间的关系
K L ( P ∥ Q ) = ∑ x p ( x ) log p ( x ) q ( x ) = ∑ x p ( x ) log p ( x ) − ∑ x p ( x ) log q ( x ) = − H ( P ) + H ( P , Q ) \qquad\qquad KL(P \parallel Q) = \sum\limits_{x}p(x)\log\cfrac{p(x)}{q(x)}\\\qquad\qquad\qquad\quad\quad\quad\ =\sum\limits_{x}p(x)\log{p(x)}-\sum\limits_{x}p(x)\log{q(x)}\\\qquad\qquad\qquad\quad\quad\quad\ =-H(P)+H(P,Q) KL(P∥Q)=x∑p(x)logq(x)p(x) =x∑p(x)logp(x)−x∑p(x)logq(x) =−H(P)+H(P,Q)
2.3 python代码实现
代码来自 https://machinelearningmastery.com/divergence-between-probability-distributions/。
2.3.1 定义两个概率分布并可视化
import matplotlib.pyplot as plt
import numpy as np
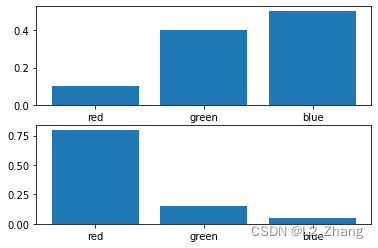
events = ['red', 'green', 'blue']
p = [0.10, 0.40, 0.50]
q = [0.80, 0.15, 0.05]
plt.subplot(2,1,1)
plt.bar(events, p)
# plot second distribution
plt.subplot(2,1,2)
plt.bar(events, q)
# show the plot
plt.show()
2.3.2 计算KL散度
2.3.2.1 自定义函数
from math import log
def kl_divergence(p, q):
return sum(p[i] * log(p[i]/q[i]) for i in range(len(p)))
# calculate (P || Q)
kl_pq = kl_divergence(p, q)
print('KL(P || Q): %.3f nats' % kl_pq)
# calculate (Q || P)
kl_qp = kl_divergence(q, p)
print('KL(Q || P): %.3f nats' % kl_qp)
#KL(P || Q): 1.336 nats
#KL(Q || P): 1.401 nats
2.3.2.2 scipy自带函数
from scipy.special import rel_entr
kl_pq = rel_entr(p, q)
print('KL(P || Q): %.3f nats' % sum(kl_pq))
# calculate (Q || P)
kl_qp = rel_entr(q, p)
print('KL(Q || P): %.3f nats' % sum(kl_qp))
#KL(P || Q): 1.336 nats
#KL(Q || P): 1.401 nats
可见scipy自带KL散度函数中log是以10为底的。
3.JS散度 Jensen-Shannon divergence
JS散度也是一种衡量两个分布相似度的指标。
3.1 定义
J S ( P ∥ Q ) = 1 2 K L ( P ∥ P + Q 2 ) + 1 2 K L ( Q ∥ P + Q 2 ) \qquad\qquad JS(P \parallel Q) =\cfrac {1}{2}\ KL(P \parallel\cfrac {P+Q}{2})+\cfrac {1}{2}\ KL(Q \parallel\cfrac{P+Q}{2}) JS(P∥Q)=21 KL(P∥2P+Q)+21 KL(Q∥2P+Q)
从公式中可以看出,JS散度具有对称性。
3.2 python代码实现
使用与前例相同的概率分布:
# calculate the js divergence
def js_divergence(p, q):
m = 0.5 * (p + q)
return 0.5 * kl_divergence(p, m) + 0.5 * kl_divergence(q, m)
p = np.asarray(p)
q = np.asarray(q)
# calculate JS(P || Q)
js_pq = js_divergence(p, q)
print('JS(P || Q) divergence: %.3f nats' % js_pq)
# calculate JS(Q || P)
js_qp = js_divergence(q, p)
print('JS(Q || P) divergence: %.3f nats' % js_qp)
#JS(P || Q) divergence: 0.291 nats
#JS(Q || P) divergence: 0.291 nats
结果表明JS散度具有对称性。
scipy中实现的是jensen-shannon距离,即JS散度的平方根值。这里不再细述。
from scipy.spatial.distance import jensenshannon
4.交叉熵 cross-entropy
交叉熵是机器学习/深度学习中分类任务/语义分割中一种常用的损失函数。
4.1 公式
H ( P , Q ) = − ∑ x p ( x ) log q ( x ) \\\qquad\qquad H(P,Q)=-\sum\limits_{x}p(x)\log{q(x)} H(P,Q)=−x∑p(x)logq(x)
如KL散度一节介绍,
H ( P , Q ) = H ( P ) + K L ( P ∥ Q ) \qquad\qquad H(P,Q)=H(P)+KL(P \parallel Q) H(P,Q)=H(P)+KL(P∥Q)
4.2 python代码实现
以下代码引自https://machinelearningmastery.com/cross-entropy-for-machine-learning/。
使用与前例相同的概率分布:
# example of calculating cross entropy
from math import log2
# calculate cross entropy
def cross_entropy(p, q):
return -sum([p[i]*log2(q[i]) for i in range(len(p))])
# define data
p = [0.10, 0.40, 0.50]
q = [0.80, 0.15, 0.05]
# calculate cross entropy H(P, Q)
ce_pq = cross_entropy(p, q)
print('H(P, Q): %.3f bits' % ce_pq)
# calculate cross entropy H(Q, P)
ce_qp = cross_entropy(q, p)
print('H(Q, P): %.3f bits' % ce_qp)
#H(P, Q): 3.288 bits
#H(Q, P): 2.906 bits
参考文献
[1] 周志华,机器学习,附录C.3 KL散度
[2] 李航,统计学习方法,5.2.2 信息增益 及 附录E KL散度的定义和…
[3] 邱锡鹏,神经网络与深度学习,附录E 信息论
[4] https://machinelearningmastery.com/divergence-between-probability-distributions/
[5] https://machinelearningmastery.com/cross-entropy-for-machine-learning/
[6] https://d2l.ai/chapter_appendix-mathematics-for-deep-learning/information-theory.html#cross-entropy