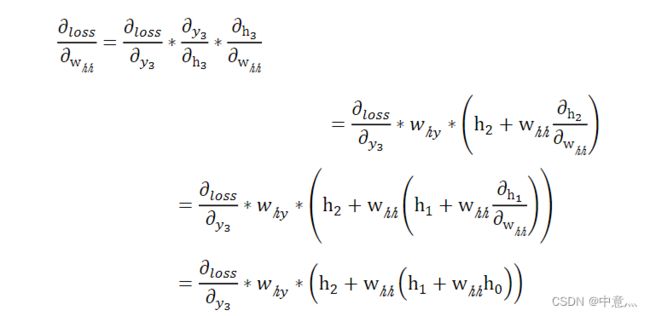基于LSTM的短期股票预测
目录
1.原始RNN的问题
2.LSTM
(1)原理
(2)Tensorflow2描述LSTM层
(3)LSTM股票预测
1.原始RNN的问题
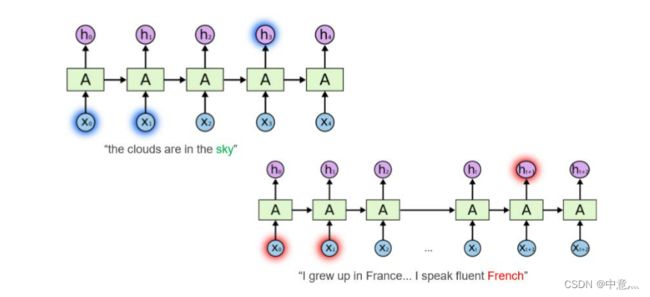
RNN面临的较大问题是无法解决长跨度依赖问题,即后面节点相对于跨度很大的前面时间节点的信息感知能力太弱,如下图中的两句话:左上角的句子中sky可以由较短跨度的词预测出来,而右下角中的French与较长跨度之间的France有关系,即长跨度依赖,比较难预测。
长跨度依赖的根本问题在于,多阶段的反向传播后导致梯度消失、梯度爆炸。可以使用梯度截断去解决梯度爆炸问题,但无法轻易解决梯度消失问题。
下面举一个例子来解释RNN梯度消失和爆炸的问题:
假设时间序列有三段,![]() 为给定值,且为了简便假设没有激活函数和偏置,则RNN得前向传播过程如下:
为给定值,且为了简便假设没有激活函数和偏置,则RNN得前向传播过程如下:
![]()
![]()
![]()
![]()
![]()
![]()
假设在t=3时刻,损失函数为![]() ,其余时刻类似。则
,其余时刻类似。则![]() 。梯度下降法训练就是对参数分别求偏导,然后按照梯度反方向调整他们使loss值变小得过程。假设只考虑t=3时刻得
。梯度下降法训练就是对参数分别求偏导,然后按照梯度反方向调整他们使loss值变小得过程。假设只考虑t=3时刻得![]() ,这里考虑
,这里考虑![]() 的偏导:
的偏导:
可以看出,只有三个时间点时,![]() 的偏导与
的偏导与![]() 的平方成正比。传统循环网络RNN可以通过记忆体实现短期记忆进行连续数据的预测,但是当连续数据的序列变长时会展开时间步长过长。当时间跨度变长时,幂次将变大。所以,如果
的平方成正比。传统循环网络RNN可以通过记忆体实现短期记忆进行连续数据的预测,但是当连续数据的序列变长时会展开时间步长过长。当时间跨度变长时,幂次将变大。所以,如果![]() 为一个大于0小于1的数,随着时间跨度的增长,偏导值将会趋于0;同理,当
为一个大于0小于1的数,随着时间跨度的增长,偏导值将会趋于0;同理,当![]() 较大时,偏导值将趋于无穷。这就是梯度消失和爆炸的原因。
较大时,偏导值将趋于无穷。这就是梯度消失和爆炸的原因。
2.LSTM
LSTM由Hochreiter&Schmidhuber于1997年提出,通过门控单元很好的解决了RNN长期依赖问题。
(1)原理
有兴趣的去看这篇文章吧,讲的很清楚也很明白了
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
(2)Tensorflow2描述LSTM层
tf.keras.layers.LSTM(
units,
activation='tanh',
return_sequences=False
)其中,units为神经元个数,activation为激活函数,默认为tanh,return_sequences为是否全部时刻返回输出,默认为False。
(3)LSTM股票预测
# -*- coding: utf-8 -*-
# @Time : 2022/10/2 15:15
# @Author : 中意灬
# @FileName: 基于LSTM的股票预测.py
# @Software: PyCharm
"""第一步:导入相关的库"""
import math
import os.path
import tensorflow as tf
import tushare as ts
import numpy as np
import tensorflow
import pandas as pd
from tensorflow.keras.layers import Dense,LSTM,Dropout
import matplotlib.pyplot as plt
from tensorflow.keras import Model
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error,mean_absolute_error
"""第二步:准备数据"""
datapath='/data.csv'
if os.path.exists(datapath):
print("==========loading data==========")
data=pd.read_csv(datapath)
training_set=data.iloc[0:2427-300,2:3]
test_set=data.iloc[2427-300:,2:3]
else:
ts.set_token('f9e62b42d9f31fbf0267d9ba52204d37c5fef60f3d6091e9820c40a1') # 这儿的token需要自己去turshare注册申请
df = ts.get_k_data('600519', ktype='D', start='2012-01-01', end='2022-01-01')
df.to_csv(datapath)
data = pd.read_csv('./data.csv')
training_set = data.iloc[0:2427 - 300, 2:3].values
test_set = data.iloc[2427 - 300:, 2:3].values
#归一化
sc=MinMaxScaler(feature_range=(0,1))#初始化对象定义归一化:归一化到(0-1)间
training_set_scaler=sc.fit_transform(training_set)#求得训练集的最大值,最小值这些训练集固有的属性(反归一化所需要这些属性),并在训练集上进行归一化
test_set=sc.transform(test_set)#利用训练集的属性对测试集进行归一化
# print(training_set_scaler)
x_train=[]
x_test=[]
y_train=[]
y_test=[]
#利用for循环,遍历整个训练集,将训练集连续60天的数据作为训练特征x_train,第61天数据作为训练标签y_train
for i in range(60,len(training_set_scaler)):
x_train.append(training_set_scaler[i-60:i,0])
y_train.append(training_set_scaler[i,0])
#将训练特征和标签转换神经网络的输入格式,使x_train符合LSTM输入要求:[送入样本数,循环核时间展开步骤,每个时间步输入特征个数]
x_train,y_train=np.array(x_train),np.array(y_train)
x_train=np.reshape(x_train,(len(x_train),60,1))
#利用for循环,遍历整个训练集,将训练集连续60天的数据作为测试特征x_test,第61天数据作为测试标签y_test
for i in range(60,len(test_set)):
x_test.append(test_set[i-60:i,0])
y_test.append(test_set[i,0])
#将测试特征和标签转换神经网络的输入格式,使x_train符合LSTM输入要求:[送入样本数,循环核时间展开步骤,每个时间步输入特征个数]
x_test,y_test=np.array(x_test),np.array(y_test)
x_test=np.reshape(x_test,(len(x_test),60,1))
"""第三步:使用class类搭建LSTM神经网络模型"""
class LSTMModel(Model):
def __init__(self):
super(LSTMModel, self).__init__()
self.l1=LSTM(256,activation='tanh',return_sequences=True)
self.d1=Dropout(0.2)
self.l2=LSTM(128,activation='tanh',return_sequences=False)
self.d2=Dropout(0.2)
self.f1=Dense(1)
def call(self,x):
x=self.l1(x)
x=self.d1(x)
x=self.l2(x)
x=self.d2(x)
x=self.f1(x)
return x
"""第四步:使用model.compile配置神经网络参数"""
model=LSTMModel()
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),#自己设定adam的学习率,尽量先设置小,大了会收敛过快
loss="mean_squared_error")#不必观察metrics值,没必要,只用观察loss值就可以
checkpoint_save_path="./checkpoint/LSTN.ckpt"
if os.path.exists(checkpoint_save_path+'.index'):
print("==========load the model==========")
model.load_weights(checkpoint_save_path)
cp_callback=tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True,
moniter='val_loss')
"""第五步:用model.fit训练神经网络模型"""
history=model.fit(x_train,y_train,batch_size=32,epochs=50,validation_data=(x_test,y_test),validation_freq=1,callbacks=[cp_callback])
#参数提取
file=open('./weights.txt','w')
for v in model.trainable_variables:
file.write(str(v.name)+'\n')
file.write(str(v.shape)+'\n')
file.write(str(v.numpy())+'\n')
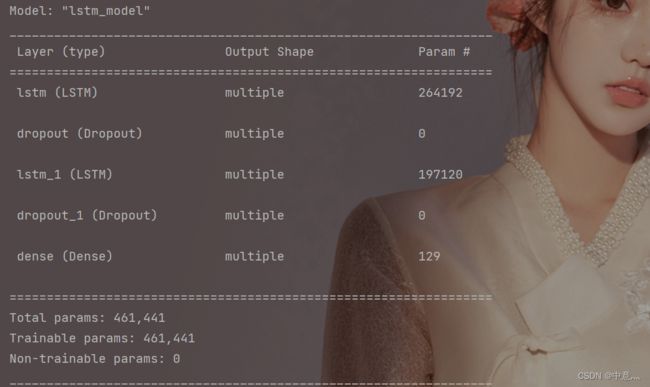
"""第六步:使用model.summary打印神经网络结构"""
model.summary()
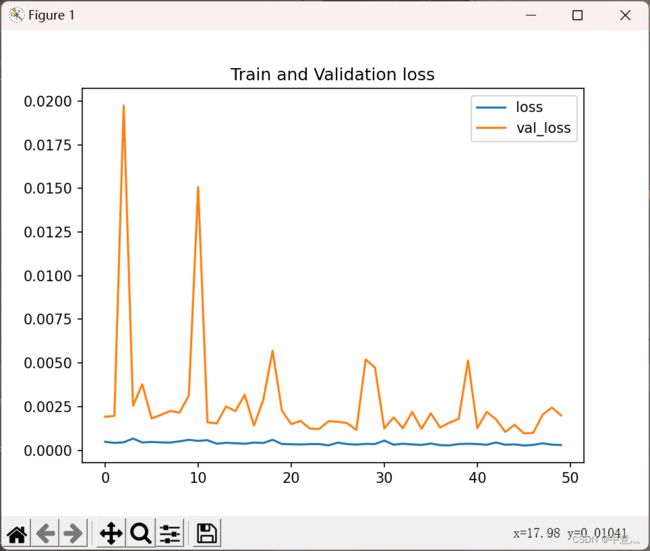
#绘制loss图像
plt.figure()
plt.plot(history.history['loss'],label='loss')
plt.plot(history.history['val_loss'],label='val_loss')
plt.title('Train and Validation loss')
plt.legend()
plt.show()
#模型预测
predict_stock_openprice=model.predict(x_test)
#对预测数据反归一化
predict_stock_openprice=sc.inverse_transform(predict_stock_openprice)
#对真实数据反归一化
real_stock_openprice=sc.inverse_transform(test_set[60:])
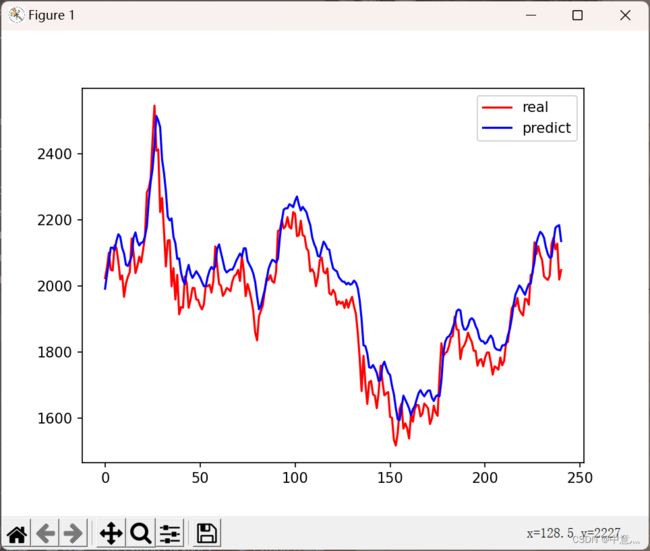
#可视化
plt.figure()
plt.plot(real_stock_openprice,color='r',label='real')
plt.plot(predict_stock_openprice,color='b',label='predict')
plt.legend()
plt.show()
##模型预测效果量化,数值越小,效果越好
#MSE 均方误差-->E[(预测值-真实值)^2]
mse=mean_squared_error(predict_stock_openprice,real_stock_openprice)
#RMSE 均方误差根-->sqrt(mse)
rmse=math.sqrt(mean_squared_error(predict_stock_openprice,real_stock_openprice))
#MAE 平均绝对误差-->E(|预测值-真实值|)
mae=mean_absolute_error(predict_stock_openprice,real_stock_openprice)
print('均方误差:',mse)
print('均方误差根:',rmse)
print('平局绝对误差:',mae)
#对未知数据预测
preNum=int(input('输入你要预测后多少个数据:'))
a = test_set[len(test_set) - 60:, 0]
c=[]#存储预测后的数据
for i in range(preNum):
b=np.reshape(a,(1,60,1))
pre=model.predict(b)
a=a.tolist()
del a[0]
a.extend(pre[0])
c.extend(pre)
a=np.array(a)
test_set=np.array(test_set)
c=sc.inverse_transform(c)
plt.figure()
plt.plot(sc.inverse_transform(test_set[60:]),color='b',label='real')
x=np.arange(len(test_set[60:]),len(test_set[60:])+preNum)
plt.plot(x,c,color='r')
plt.plot(predict_stock_openprice,color='r',label='predict')
plt.show()训练集损失