无向图最小生成树（两种做法）

最小生成树（MST）：权值最小的生成树。

构造网的最小生成树必须解决下面两个问题：
1、尽可能选取权值小的边，但不能构成回路；
2、选取n－1条恰当的边以连通n个顶点；

MST性质：假设G＝(V,E)是一个连通网，U是顶点V的一个非空子集。若(u,v)是一条具有最小权值的边，其中u∈U，v∈V－U，则必存在一棵包含边(u,v)的最小生成树。

1.prim算法
基本思想：假设G＝(V，E)是连通的，TE是G上最小生成树中边的集合。算法从U＝{u0}（u0∈V）、TE＝{}开始。重复执行下列操作：

在所有u∈U，v∈V－U的边(u，v)∈E中找一条权值最小的边(u0,v0)并入集合TE中，同时v0并入U，直到V＝U为止。

此时，TE中必有n-1条边，T=(V，TE)为G的最小生成树。

Prim算法的核心:始终保持TE中的边集构成一棵生成树。

注意：prim算法适合稠密图，其时间复杂度为O(n^2)，其时间复杂度与边得数目无关。

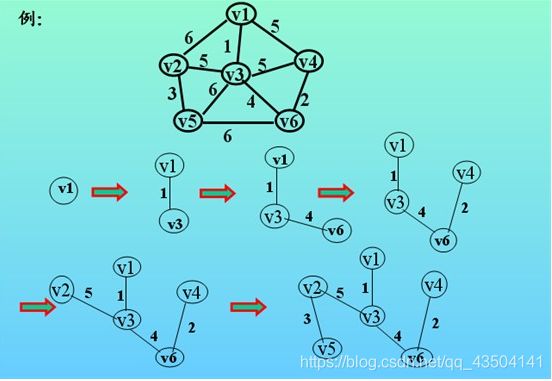
1）图中有6个顶点v1-v6，每条边的边权值都在图上；在进行prim算法时，我先随意选择一个顶点作为起始点，当然我们一般选择v1作为起始点，好，现在我们设U集合为当前所找到最小生成树里面的顶点，TE集合为所找到的边，现在状态如下：

U={v1}； TE={}；

（2）现在查找一个顶点在U集合中，另一个顶点在V-U集合中的最小权值，如下图，在红线相交的线上找最小值。

通过图中我们可以看到边v1-v3的权值最小为1，那么将v3加入到U集合，（v1，v3）加入到TE，状态如下：

U={v1，v3}； TE={（v1，v3）}；

（3）继续寻找，现在状态为U={v1，v3}； TE={（v1，v3）}；在与红线相交的边上查找最小值。

我们可以找到最小的权值为（v3，v6）=4，那么我们将v6加入到U集合，并将最小边加入到TE集合，那么加入后状态如下：

U={v1，v3，v6}； TE={（v1，v3），（v3，v6）}； 如此循环一下直到找到所有顶点为止。

（4）下图像我们展示了全部的查找过程：

克鲁斯卡尔（Kruskal）算法（只与边相关）
算法描述：克鲁斯卡尔算法需要对图的边进行访问，所以克鲁斯卡尔算法的时间复杂度只和边又关系，可以证明其时间复杂度为O（eloge）。

算法过程：

1.将图各边按照权值进行排序

2.将图遍历一次，找出权值最小的边，（条件：此次找出的边不能和已加入最小生成树集合的边构成环），若符合条件，则加入最小生成树的集合中。不符合条件则继续遍历图，寻找下一个最小权值的边。

3.递归重复步骤1，直到找出n-1条边为止（设图有n个结点，则最小生成树的边数应为n-1条），算法结束。得到的就是此图的最小生成树。判断是否构成环：《算法导论》提供的一种方法是采用一种"不相交集合数据结构"，也就是并查集了。核心内容就是如果某两个节点属于同一棵树，那么将它们合并后一定会形成回路。

克鲁斯卡尔（Kruskal）算法因为只与边相关，则适合求稀疏图的最小生成树。而prime算法因为只与顶点有关，所以适合求稠密图的最小生成树。

prim算法：

#include 
#include 
#include 
#include 
#define N 1005
#define inf 0x3f3f3f3f
#define mem(a) memset(a,0,sizeof(a))
using namespace std;
int cost[N][N];//表示两点之间的距离,不存在则设为inf
int mincost[N];//从x集合出发到每个顶点的最小值
bool used[N];//判断是否在集合中的布尔数组
int n,m;

int prim(){
  for(int i=0;i<n;i++){//初始化mincost数组和used布尔数组
    mincost[i]=inf;
    used[i]=false;
  }
  mincost[0]=0;//赋给其初值
  long long int ans=0;

  while(true){
    int v=-1;
    //从不属于x的顶点中选取从x到其权值最小的顶点
    for(int u=0;u<n;u++)
      if(!used[u]&&(v==-1||mincost[u]<mincost[v]))
        v=u;

    if(v==-1)
      break;//条件成立则说明所有的点都已经加入
    used[v]=true;//把顶点加入
    ans+=mincost[v];//把边的长度加到结果里

    for(int u=0;u<n;u++){
      if(!used[u])
        mincost[u]=min(mincost[u],cost[v][u]);
    }
  }
  return ans;
}
int main(){
  cin>>n>>m;
  int x,y,z;
  memset(cost,inf,sizeof(cost));
  while(m--){
    scanf("%d%d%d",&x,&y,&z);
    cost[--x][--y]=z;
    cost[y][x]=z;
  }
  long long int k=prim();
  cout<<k<<endl;
  return 0;
}

kruskal算法解题:

#include 
#include 
#include 
#include 
#define N 50005
using namespace std;
struct Node{//定义结构体,分别加入两个点和两个点之间的权值
 int u,v,cost;
};
bool cmp(Node a,Node b){//自定义排序
 return a.cost<b.cost;
}
Node node[N];
int fa[N];
int n,m;
int Find(int x){//并查集查找
 return x==fa[x]?x:Find(fa[x]);
}
void init(){//初始化fa数组
 for(int i=0;i<n;i++){
   fa[i]=i;
 }
 return ;
}
int kruskal(){
 init();
 long long int cnt=0;
 int t=0;
 for(int i=0;i<m;i++){
   Node e=node[i];
   int x=Find(e.u);
   int y=Find(e.v);
   if(x!=y){//如果父节点相同,则构成了一个环,那么就不能将其放入里面,跳过
     fa[x]=y;
     cnt+=e.cost;
     t++;
   }
   if(t==n-1) break;//如果所加的边达到了n-1条,跳出循环
 }
 return cnt;
}
int main(){
 scanf("%d%d",&n,&m);
 for(int i=0;i<m;i++){
   scanf("%d%d%d",&node[i].u,&node[i].v,&node[i].cost);
 }
 sort(node ,node+m,cmp);
 long long int ans=kruskal();
 printf("%lld\n",ans);
 return 0;
}