二叉树的遍历

---

二叉树

基本介绍

定义：

二叉树（binary tree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树 。——百度百科

特殊类型

1、满二叉树：如果一棵二叉树只有度为0的节点和度为2的节点，并且度为0的节点在同一层上，则这棵二叉树为满二叉树 。

2、完全二叉树：深度为k，有n个节点的二叉树当且仅当其每一个节点都与深度为k的满二叉树中编号从1到n的节点一一对应时，称为完全二叉树 。

完全二叉树的特点是叶子节点只可能出现在层序最大的两层上，并且某个节点的左分支下子孙的最大层序与右分支下子孙的最大层序相等或大1 。

二叉树的性质

性质1：二叉树的第i层上至多有2i-1（i≥1）个节点 。

性质2：深度为h的二叉树中至多含有2h-1个节点 。

性质3：若在任意一棵二叉树中，有n0个叶子节点，有n2个度为2的节点，则必有n0=n2+1 。

性质4：具有n个节点的满二叉树深为log2n+1。

性质5：若对一棵有n个节点的完全二叉树进行顺序编号（1≤i≤n），那么，对于编号为i（i≥1）的节点：

当i=1时，该节点为根，它无双亲节点 。

当i>1时，该节点的双亲节点的编号为i/2 。

若2i≤n，则有编号为2i的左节点，否则没有左节点 。

若2i+1≤n，则有编号为2i+1的右节点，否则没有右节点 。

二叉树的四种遍历方式

复杂性：

设二叉树中元素数目为n。这四种遍历算法的空间复杂性均为O (n)，时间复杂性为O(n)。

(1)前序遍历

前序遍历：根左右（DFS深搜顺序）

前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树。

若二叉树为空则结束返回，否则：

（1）访问根结点。

（2）前序遍历左子树。

图1 前序遍历

（3）前序遍历右子树 。

需要注意的是：遍历左右子树时仍然采用前序遍历方法。

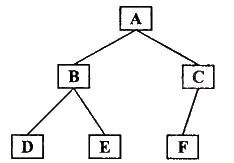
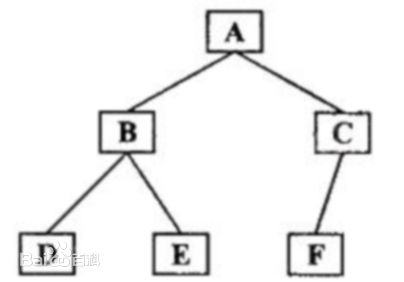
前序遍历结果：ABDECF

已知后序遍历和中序遍历，就能确定前序遍历。

(2)中序遍历

中序遍历：左根右

中序遍历（LDR）是二叉树遍历的一种，也叫做中根遍历、中序周游。在二叉树中，中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。

中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。若二叉树为空则结束返回，否则：

图1

（1）中序遍历左子树

（2）访问根结点

（3）中序遍历右子树

如图1所示二叉树，中序遍历结果：DBEAFC

(3)后序遍历

后序遍历：左右根

后序遍历首先遍历左子树，然后遍历右子树，最后访问根结点，在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后遍历根结点。即：

若二叉树为空则结束返回，

图1

否则：（1）后序遍历左子树

（2）后序遍历右子树

（3）访问根结点

如图1所示二叉树

后序遍历结果：DEBFCA

已知前序遍历和中序遍历，就能确定后序遍历。

(4)层序遍历

层序遍历：一层一层的搜（BFS）

二叉树的层次遍历 ，顾名思义就是指从二叉树的第一层（根节点）开始，从上至下逐层遍历，在同一层中，则按照从左到右的顺序对节点逐个访问。在逐层遍历过程中，按从顶层到底层的次序访问树中元素，在同一层中，从左到右进行访问。

算法思想：（BFS）宽搜过程

用一个队列保存被访问的当前节点的左右孩子以实现层序遍历。

在进行层次遍历的时候，设置一个队列结构，遍历从二叉树的根节点开始，首先将根节点指针入队列，然后从队头取出一个元素，每取一个元素，执行下面两个操作：

1、访问该元素所指向的节点

2、若该元素所指节点的左右孩子节点非空，则将该元素所指节点的左孩子指针和右孩子指针顺序入队。此过程不断进行，当队列为空时，二叉树的层次遍历结束。

图1

层序遍历结果：ABCDEF

巩固练习

树的遍历

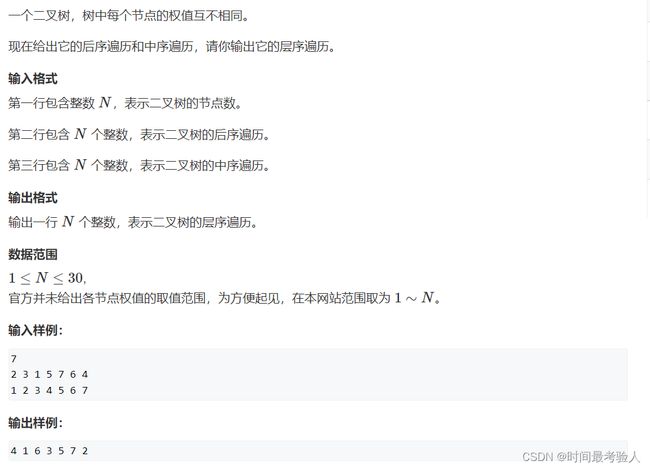
【题目链接】1497. 树的遍历 - AcWing题库

思路：

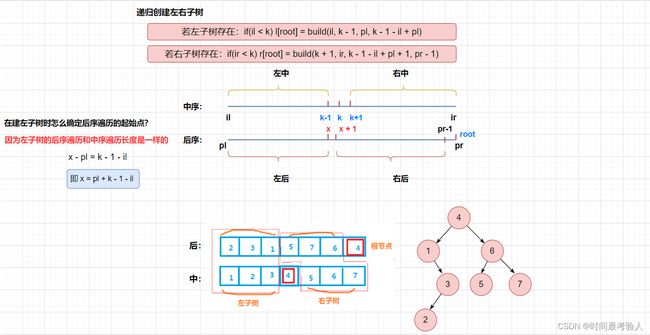
如何由中序和后序确定一棵二叉树

① 中序遍历可以与前序遍历、后序遍历和层次遍历中的任意一个来构建唯一的二叉树，而后三者两两搭配或者是三个一起上都无法创建一颗唯一的一颗二叉树，原因是先序、后序、层次遍历均是提供根节点，作用是相同的，都必须由中序遍历来区分出左子树与右子树，所以中序遍历与后序遍历可以唯一确定一棵二叉树

② 首先是要先确定二叉树的根，确定二叉树的根可以在二叉树的后序遍历序列中去找，后序遍历中最后一个节点就是根节点，然后再在中序遍历中找到根节点区分出左子树与右子树
即：

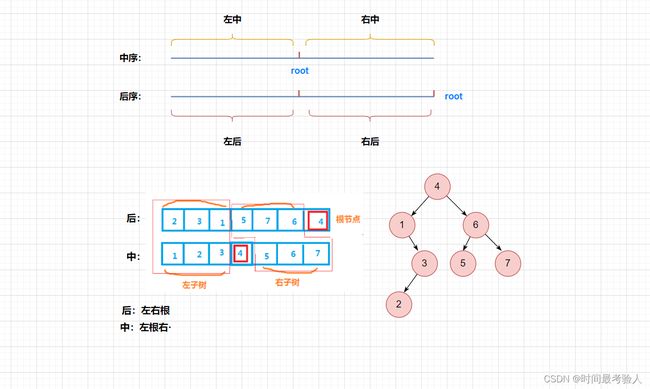
1.后序遍历的最后一定是该树或子树的根
2.中序遍历根的左右分左子树和右子树
所以可以通过后序遍历找到根的值，然后再到中序序列里找到根的位置再将该树分为左子树与右子树 然后不断递归即可通过中序和后序重塑一棵树.

具体步骤：

1.先根据后序和中序遍历结果构造二叉树

存储结构使用两个哈希表：leftChile, rightChile。leftChile[i] = j: i 的左儿子是j,rightChilet同理后序遍历的最后一个节点是跟节点，得到根节点后，递归构造根节点的左儿子和右儿子。

返回二叉树的根节点

2.按层次遍历构造出来的二叉树（BFS）

【代码实现】

#include 
#include 
#include 
#include 
#include 

using namespace std;

const int N = 40;
int inorder[N], postorder[N];// 前序和后序序列
//哈希表保存树，l[root] = x: root 的左儿子是x,r同理
unordered_map<int, int> l, r;// 哈希表建树（左右子树）———— 存每个点的左儿子和右儿子
unordered_map<int, int> pos; // 记录节点的位置，方便在中序遍历中找到根节点的位置
int n;
// il, ir为中序遍历的起终点位置 pl, pr为后序遍历的起终点位置
int build(int il, int ir, int pl, int pr)// 返回根节点（返回选中的前和后遍历段的根节点！）
{
    int root = postorder[pr];// 拿到后序遍历的根节点
    int k = pos[root];// 得到根节点在中序遍历中的位置（下标）
    
    // 在存在的情况下递归创建左右子树
    if(il < k) l[root] = build(il, k - 1, pl, pl + k - 1 - il);
    if(ir > k) r[root] = build(k + 1, ir, pl + k - il, pr - 1);
    
    return root;
    
}

// bfs输出层序遍历结果
void bfs(int root)
{
    queue<int> q;
    q.push(root);
    
    while(q.size())
    {
        auto t = q.front();
        q.pop();
        
        cout << t << ' ';
        
        if(l.count(t)) q.push(l[t]);// 若果左子树存在，左儿子入队
        if(r.count(t)) q.push(r[t]);// 如果右子树存在，右儿子入队
    }
}


int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ ) cin >> postorder[i];
    for(int i = 0; i < n; i ++)
    {
        cin >> inorder[i];
        pos[inorder[i]] = i;
    }
    int root = build(0, n - 1, 0, n - 1);//拿到树的根节点
    bfs(root);// 宽搜得到层序遍历结果
    
    return 0;
}

美国传统

【题目链接】1389. 美国传统 - AcWing题库

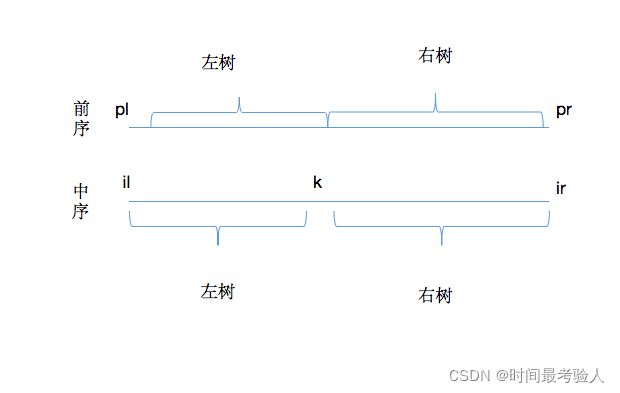
先用哈希表记录中序遍历中每个字母的位置，以便在递归时能准确知道根节点在中序遍历中的位置，然后分别递归中序遍历的左子树、前序遍历的左子树 和 中序遍历的右子树、前序遍历的右子树，以保证所得到的序列是后序遍历的结果。

前序的pl位置为根节点, 对应中序的k的位置。
那么中序遍历的左树部分：il 到 k - 1;
那么中序遍历的右树部分：k + 1 到 ir;
那么前序遍历的左树部分：pl + 1 到 pl + 1 + k - 1 - il;
那么前序遍历的右树部分：pl + 1 + k - 1 - il + 1 到pr;

通过哈希表快速查找前序遍历字符对应中序遍历哪个位置。

【代码实现】

#include 
#include 
#include 
#include 
#include 

using namespace std;

const int N = 30;

string qian, zhong, hou;
unordered_map<char, int> pos;

//         zhong           qian
void build(int il, int ir, int pl, int pr)// 后序：左右根
{
    if(il > ir ) return ;
    
    int root = qian[pl];
    int k = pos[root];
    
    // 左子树
    // x - (pl + 1) = k - 1 - il
    build(il, k - 1, pl + 1, k - 1 -il + pl + 1);
    build(k + 1, ir, k - 1 -il + pl + 1 + 1, pr);
    hou += qian[pl];
}

int main()
{
    cin >> zhong >> qian;
    
    int n = zhong.size();
    for (int i = 0; i < n; i ++ ) pos[zhong[i]] = i;
    
    build(0, n - 1, 0, n - 1);
    
    cout << hou;
    
    
    return 0;
}

构建二叉搜索树

定义：

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

性质：

设x是二叉搜索树中的一个结点。如果y是x左子树中的一个结点，那么y.key≤x.key。如果y是x右子树中的一个结点，那么y.key≥x.key。

在二叉搜索树中：

1.若任意结点的左子树不空，则左子树上所有结点的值均不大于它的根结点的值。

2.若任意结点的右子树不空，则右子树上所有结点的值均不小于它的根结点的值。

3.任意结点的左、右子树也分别为二叉搜索树。

二叉搜索树的一大特点即为，其**中序遍历的结果为所有节点值的升序排列。**

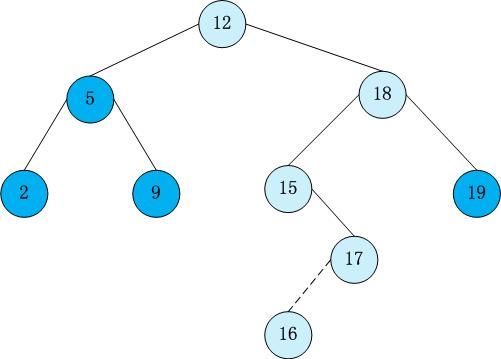
【题目链接】1589. 构建二叉搜索树 - AcWing题库

思路：

• 将原数组排序，然后将序列按照中序遍历的顺序（左根右）将所有数填到树里边即可（递归填数）！
• bfs输出层序遍历结果

【代码实现】

#include 
#include 
#include 
#include 

using namespace std;

const int N = 110;
int n, k;
int l[N], r[N], inorder[N];//左子树，右子树， 权值 
int a[N];

// 实现中序遍历：左根右
void dfs(int u)
{
    if(u == -1) return ;// 当前节点为空
    
    dfs(l[u]);// 左！
    inorder[u] = a[k ++];// 根！ a[]数组经过排序了！当前节点的权值为a[k ++]
    dfs(r[u]);// 右！
    
}
// // 实现中序遍历：左根右
// void dfs(int u)
// {
    
//     if(l[u] != -1)// 左子树不为空
//         dfs(l[u]);// 左！
        
//     inorder[u] = a[k ++];// 根！ a[]数组经过排序了！当前节点的权值为a[k ++]
    
//     if(r[u] != -1)// 左子树不为空
//         dfs(r[u]);// 右！
    
// }


// 输出二叉搜索树的层序遍历结果
void bfs()
{
    queue<int> q;
    q.push(0);// 根节点入队
    while(q.size())
    {
        auto t = q.front();
        q.pop();
        
        cout << inorder[t] << " ";
        if(l[t] != -1) q.push(l[t]);// 存在左儿子
        if(r[t] != -1) q.push(r[t]);// 存在右儿子
        
    }
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ ) cin >> l[i] >> r[i];
    for (int i = 0; i < n; i ++ ) cin >> a[i];
    sort(a, a + n);// 排序
    
    dfs(0);// 从第0个位置开始填
    
    bfs();
    
    return 0;
}

FBI树

【题目链接】419. FBI树 - AcWing题库

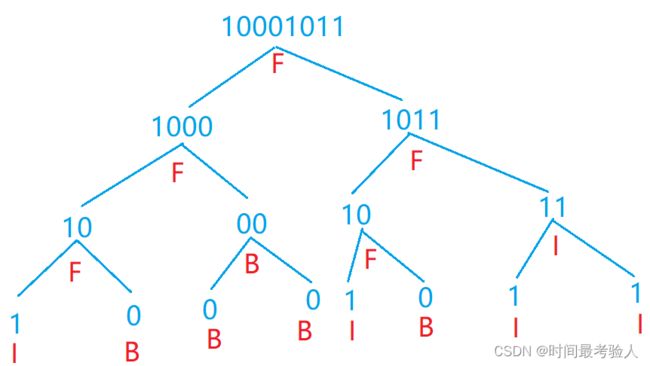
对于样例来说，我们可以得到如下所示的满二叉树：

可以递归处理整棵树，我们发现当输入字符串固定时，整棵树也就固定了，因此可以将字符串当做递归函数传入的参数。

由于要输出后序遍历，因此需要先输出左子树和右子树，再输出当前节点的信息。

从图中可以发现，左子树所对应的字符串即是当前字符串的前半段，右子树所对应的字符串是后半段。因此依次递归处理字符串的前半段和后半段即可。

最后需要判断当前节点的类型，这里可以统计一下当前字符串中0和1的包含情况。

【代码实现】

#include 
#include 
#include 

using namespace std;

int n;
string s;

// 模拟后序遍历
void dfs(string str)
{
    if(str.size() > 1)
    {
        dfs(str.substr(0, str.size() / 2)); // 左
        dfs(str.substr(str.size()/ 2));// 右
    }
    // 根
    int one = 0, zero = 0;
    for (int i = 0; i < str.size(); i ++ )
        if(str[i] == '0') zero ++;
        else one ++;
        
    //全 0 串称为 B 串，全 1 串称为 I 串，既含 0 又含 1 的串则称为 F    
    if(zero && one) cout << 'F';
    else if(zero && one == 0) cout << 'B';
    else cout << 'I';
}

int main()
{
    cin >> n;
    cin >> s;
    
    dfs(s);
    
    return 0;
}

总结

学习二叉树是理解递归过程的一个很好的途径，要理解掌握二叉树的构建以及遍历过程顺序等等

参考文献：

acwing题库

百度百科